 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Перестановки с повторением:
Комбинаторика. Комбинаторика— специальный раздел математики, изучающий задачи составления тех или иных комбинаций из заданного множества элементов.
Размещения
Пусть имеется множество, содержащее т элементов. Сколькими способами можно составить подмножества из п элементов, то их число называется размещением из т элементов по п элементов (0 ≤ п ≤ т). Для подсчета числа всех размещений и обозначения этого числа применяется специальный символ Т.е., если в комбинации из т элементов по п важен и состав, и порядок следования, то это – размещение.
Пример. Сколько различных комбинаций по 2 буквы можно составить из 5 разных букв: А,Б,В,Г,Д? АБ АВ АГ АД БА БВ БГ БД ВА ВБ ВГ ВД ГА ГБ ГВ ГД ДА ДБ ДВ ДГ или Пример. Изучается 12 дисциплин. Сколькими способами можно составить расписание лекций, если в этот день должны быть три различные лекции? Различных вариантов составления расписания лекций, очевидно, столько, сколько существует трехэлементных упорядоченных подмножеств у 12-элементного множества. То есть число вариантов равно числу размещений из 12 элементов по 3. По формуле Пример. В группе 30 студентов. Сколькими способами могут быть выбраны староста и его заместитель?По условию задачи каждый студент может быть выбран старостой, то, следовательно, существует 30 вариантов выбора старосты. Его заместителем может стать любой из оставшихся 29 студентов. Таким образом, любой из 30 вариантов выбора старосты может осуществляться вместе с любым из 29 вариантов выбора его заместителя. Следовательно, существует 30 · 29 = 870 вариантов выбора. Или по формуле:
Если рассматривать число размещений, где будут учитываться комбинации с повторениями, то число таких размещений из т элементов по п в каждом подмножестве обозначают Т.е., если в размещениях из т элементов по п некоторые из элементов (или все) могут оказаться одинаковыми, то такие размещения называют размещениями с повторениями из т элементов по п. Пример. число размещений для предыдущего примера составит Пример. Абонент забыл две последние цифры номера телефона и набирает их наудачу. Каково наибольшее число безуспешных попыток? В каждой из двух позиций может оказаться любая цифра от нуля до девяти. Следовательно, общее число возможных комбинаций составит 10 х 10 = 100. Одна из них будет верной. Из чего следует, количество безуспешных попыток будет равно: 100 - 1 = 99 или по формуле Перестановки Перестановки являются частным случаем размещений, т. к. любая перестановка содержит все n элементов множества, а различные перестановки отличаются друг от друга только порядком элементов. Перестановкамииз п различных элементов называются все возможные последовательности этих п элементов. Число перестановок без повторений из п элементов обозначают символом Рn и подсчитывают так: Рn = n! = 1·2·... ·n . Т.е., если в комбинации из т элементов по п важен только порядок следования, то это – перестановка. Пример. Сколькими способами можно составить трехцветный флаг?Флаг представляет собой три сшитые полосы материала разного цвета. Следовательно, если в этой комбинации поменять цвета местами, то получим другой флаг, отличный от первого. Всего можно получить Р3 = 3! =1·2·3 = 6 различных флагов. Пример.Порядок выступления семи участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно? Каждый вариант жеребьевки отличается только порядком участников конкурса, т.е. является перестановкой из семи элементов. Их число по формуле Р7 = 7! = 1·2·3·4·5·6·7 = 5040. Перестановки с повторением: Пусть n1-число элементов 1-го типа, n2-число элементов 2-го типа, ………. nk -число элементов k-ro типа и Перестановками с повторением из п элементов к типов (к ≤ п) называются все возможные последовательности исходных n элементов. Число перестановок с повторениями обозначают символом Пример.Перестановки элементов с повторениями из п = 3: а,а,b двух типов («а» повторяется п1 = 2 раза, «b» повторяется п2 = 1 раз), таковы: aab; aba; baa. Число перестановок равно 3. И согласно формуле получим такой же результат: Пример.У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано? Решение. Имеем набор {я, я, г, г, г}. Всего перестановок пятиэлементного множества 5!, но мы не должны учитывать перестановки, в которых объекты одного типа меняются местами несколько раз, поэтому нужно поделить на возможное число таких перестановок: 2! · 3!. Получаем в итоге
Сочетания Если имеется множество, состоящее из т элементов, и при этом рассматривается каждое его подмножество, содержащее n элементов, в котором нас интересует не порядок элементов в комбинации, а лишь ее состав, называется сочетанием из т элементов по п элементов (0≤ n ≤ т). Итак, сочетаниями из т элементов по п элементов называют всевозможные n подмножества, составленные из этих элементов и отличающиеся друг от друга составом, но не порядком элементов. Число п сочетаний, которые можно составить из т элементов, обозначается символом Т.е., если в комбинации из т элементов по п неважен порядок следования, то это – сочетание.
Пример.Если в решении задачи (Сколько различных комбинаций по 2 буквы можно составить из 5 разных букв: А,Б,В,Г,Д?) убрать комбинации АА, ББ, ВВ, ГГ, ДД и комбинации с одними и теми же символами: АБ и БА, то получим число сочетаний из 5 элементов по 2:
Пример.Всоревнованиях участвуют 10 команд. Сколько встреч проведено на этих соревнованиях? Встреч будет столько, сколько существует двухэлементных подмножеств у множества, содержащего 10 элементов, в результате получаем Пример.Сколько команд по 5 человек можно составить из 12 человек? Пример.В урне 10 белых шаров и 5 черных. · Сколькими способами можно вынуть наугад 3 белых шара? Число сочетаний из 10 по 3: · Сколькими способами можно вынуть наугад 3 черных шара? Число сочетаний из 5 по 3: · Сколькими способами можно вынуть наугад 2 белых и 1 черный шар? Число сочетаний из 10 по 2, умноженное на число сочетаний из 5 по 1: · Сколькими способами можно вынуть наугад 1 белый и 2 черных шара? Число сочетаний из 10 по 1, умноженное на число сочетаний из 5 по 2:
Если в сочетаниях из т элементов по п некоторые из элементов (или все) могут оказаться одинаковыми, то такие сочетания называют сочетаниями с повторениямииз т элементов по п инаходятся по формуле
Пример.Если в решении задачи (Сколько различных комбинаций по 2 буквы можно составить из 5 разных букв: А,Б,В,Г,Д?) добавить комбинации АА, ББ, ВВ, ГГ, ДД, то получим число сочетаний из 5элементов по 2 с повторениями: АБ, АВ, АГ, АД, БВ, БГ, БД, ВГ, ВД, ГД, АА, ББ, ВВ, ГГ, ДД. Или ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Первоначальным понятием теории вероятностей является понятие "событие". Оно считается основным, не подлежащим определению. События обозначаются заглавными латинскими буквами. Для определения вероятностей события сущ-ют различные подходы: · вер-ть м. рассматриваться в статистическом смысле (как относительная частота появления события при каком-то кол-ве испытаний). Отношение т/п числа т опытов, в которых событие А появилось, к общему числу п проведенных опытов называется частотой события А. При многократном повторении опыта частота события принимает значения, близкие к некоторому числу. Так, испытания, проведенные математиками в XVIII в. с бросанием однородной монеты, показали, что частота выпадения герба незначительно отличалась от числа 0,5.
Пример. Простейший опыт — подбрасывают монету. Выпадение герба или цифры, конечно, чисто случайное явление. Но при многократном подбрасывании обычной монеты можно заметить, что появление герба происходит примерно в половине случаев. Кто и когда впервые проделал опыт с монетой, неизвестно. Французский естествоиспытатель Ж. Л. Л. Бюффон (1707— 1788) в восемнадцатом столетии 4.040 раз подбрасывал монету — герб выпал 2048 раз. Математик К. Пирсон в начале нынешнего столетия подбрасывал ее 24.000 раз — герб выпал 12.012 раз. Лет 20 назад американские экспериментаторы повторили опыт. При 10.000 подбрасываний герб выпал 4.979 раз. Значит, результаты бросаний монеты, хотя каждое из них и является случайным событием, при неоднократном повторении подвластны объективному закону. Пример. Парадокс де Мере. В результате многократных наблюдений игры в кости француз де Мере подметил, что при одновременном бросании трех игральных костей более часто выпадает комбинация, дающая в сумме 11 очков, чем комбинация, дающая в сумме 12 очков, хотя — с его точки зрения — эти комбинации были равновероятны. Де Мере рассуждал следующим образом: 11 очков можно получить 6 способами 6-4-1, 6-3-2, 5-5-1, 5-4-2, 5-3-3, 4-4-3, и столькими же способами можно получить 12 очков 6-5-1, 6-4-2, 6-3-3, 5-5-2, 5-4-3, 4-4-4, а это означает равенство их вероятностей. Ошибка де Мере была указана знаменитым Паскалем, который заметил, что рассматриваемые де Мере исходы в данной задаче не являются равновероятными. Нужно учитывать не только выпадающие очки, но и то, на каких именно костях они выпали. Комбинации 6-4-1 соответствует один из шести исходов (6,4,1), (6,1,4), (4,6,1), (4,1,6), (1,6,4), (1,4,6), комбинация 5-5-1 выпадает лишь при трех исходах (5,5,1), (5,1,5) и (1,5,5),а комбинация 4-4-4 выпадает лишь при одном-единственном исходе (4,4,4). Итак. Событию «сумма выпавших очков равна 11» благоприятствуют ? 27 исходов, а событию «сумма выпавших очков равна 12» благоприятствуют лишь ? 25 исходов. Это и объясняет подмеченную де Мере тенденцию к более частому выпадению 11 очков. · геометрическая вер-ть. Здесь число всевозможных исходов бесконечно. Пример: вер-ть попадания точки в некоторую область, например, на острове (как отношение площадей). Пример: вер-ть обрыва провода на участке 30-35 км, если известно, что обрыв на 20-70км (как отнош. длин) · классический подход к определению вер-ти. Вероятностью случайного событияА называется отношение числа равновозможных событий, благоприятствующих этому событию, к числу всех равновозможных событий. Обозначается вероятность события А: р(А). Пример. Подбрасывают две игральные кости. Найти вероятность того, что на них в сумме выпадает шесть очков (событие А). При подбрасывании двух игральных костей общее число равновозможных элементарных исходов равно 6·6=36. Событию А благоприятствуют пять пар: (1; 5), (2; 4), (3; 3), (4; 2), (5; 1), т.е. т = 5. Следовательно, искомая вероятность р(А) = 5 / 36. Пример. Таня и Ваня хотели сидеть за праздничным столом рядом. Какова вероятность исполнения их желания, если среди их друзей принято места распределять путем жребия? Все могут усесться за стол 2·9! разными способами (Таня и Ваня, сидя рядом, считаются за 1 чел. и она могу меняться местами). Следовательно, Р = 2·9! / 10! = 1/5. Пример. В урне 5 белых и 7 черных шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара белые (событие А)? Здесь число элементарных событий Число случаев, благоприятствующих событию А: Пример.На каждой из 7 одинаковых карточек напечатана одна из следующих букв: а, г, к, и, н, р, с. Найти вероятность того, что на пяти взятых наугад и расположенных в ряд карточках можно будет прочитать слово "книга" (событие А). Общее число возможных элементарных исходов Пример.В соревнованиях по бегу участвуют 20 перворазрядников и 5 мастеров спорта. На стартовую позицию наугад последовательно вызываются два участника. Найти вероятность того, что оба участника соревнований мастера спорта (событие А). Здесь число элементарных событий п Число случаев, благоприятствующих событию А Следовательно, вероятность равна: р(А) = 10/300 = 0,033 Пример.В урне 8 белых и 12 черных шаров. Из урны наугад вынимают 6 шаров. Найти вероятность того, что среди них будет 4 белых, а, следовательно, 2 - черных шара. Р(А) =
Классификация событий Достоверное- событие, которое при соблюдении некоторых условий произойдет обязательно. Например, после ночи обязательно будет утро. Невозможное - событие, которое при соблюдении некоторых условий не может произойти. Например, после зимы сразу не наступит лето. Неопределенное - событие, результат которого заранее не может быть предсказан. Совместимые: события А, и В называются совместимыми при данном испытании, если исход одного не исключает возможности появления другого. Например, появление облачности не исключает появления дождя. Несовместимые: события А и Вназываются несовместимыми, если появление одного из них исключает возможность появления другого. Например, из коробки, содержащей два яблока разного сорта, вытаскивается одно яблоко. Вероятность того, что оно окажется первого и второго сорта, - событие несовместимое. Зависимые: события А и Взависимы, если исход события А зависит от исхода события В. Случайные события являются зависимыми друг от друга, если вероятность появления одного из них зависит от появления или непоявления другого события. Например, вероятность появления дождя зависит от вероятности появления тучи. Независимые: события А и В независимы, если исход одного из них никак не влияет на возможность появления другого. Случайные события являются независимыми друг от друга, если вероятность появления одного из них не зависит от появления или непоявления другого события. Например, в урне п белых и т черных шаров. Из урны вынимают подряд два шара. Какова вероятность того, что оба шара белые, если первый извлеченный шар вновь возвращается в урну? События, что оба извлеченных шара белые, независимы.
Итак. Любому случайному событию А соответствует определенное число р(А), удовлетворяющее условию 0≤р(А) ≤ 1. Это число называется вероятностью события А.
|
(читается так: "число размещений из т элементов по п элементов"): 
= 
=20.
, полагая в ней т=12, п=3, находим 
= 
.
= 
.
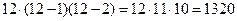и вычисляют по следующей формуле: 
= 52 = 25 комбинаций (добавятся АА ББ ВВ ГГ ДД).
.
и подсчитывают его так: 
.
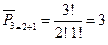
(читается: "число сочетаний из т элементов по п), и вычисляется формуле: 
.
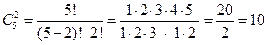или АБ, АВ, АГ, АД, БВ, БГ, БД, ВГ, ВД, ГД.
.
команд.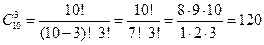
способов.
способов.
способов.
способов.
.
= 66.
® Р(А) = 
.
, а благоприятствует событию А лишь один, т. е. m = 1. Поэтому вероятность события равна: Р(А) = 
.
