 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Воспроизведите ход доказательства и комментарии к доказательству
Правило условного силлогизма
Правило modus tollens
Правило отрицания дизъюнкции (ОД)
Правило отрицания конъюнкции (ОК)
Правило контрапозиции 1
Правило контрапозиции 2
Правило сложной контрапозиции
Правило простой конструктивной дилеммы (П.К.Д.)
Правило сложной конструктивной дилеммы (С.К.Д.)
Правило простой деструктивной дилеммы (П.Д.Д.)
Правило сложной деструктивной дилеммы (С.Д.Д.)
11. Упражнение
9. Список названий правил вывода 1. ВК: 2. ВД1: 3. УД2: 4. УИ2: 5. УЭ1: 6.
10. Список схем правил вывода
1.
11. Список схем правил вывода с пропущенным выводом
где А(t) – результат правильной подстановки термина t вместо x в А(х); где А(х) – результат правильной подстановки переменной х вместо y в А(y); x, a1, a2,…, an отмечены, причем переменная x безотносительно отмечена, а переменные a1, a2,…, an отмечены относительно x. Пояснения 1. Буквами A и В при формулировке правил обозначаются формулы. Выражение А(у) обозначает формулу, имеющую свободное вхождение переменной у, a A(t) — формулу, имеющую вхождение терма t, причем если t — переменная, то A(t) — формула, имеющая свободное вхождение этой переменной, а если t — индивидная константа, то A(t) — формула, содержащая эту константу. 2. Названия правил вывода расшифровываются так: ВК — введение конъюнкции, УК — удаление конъюнкции, OK —отрицание конъюнкции, ВД — введение дизъюнкции, УД — удаление дизъюнкции, ОД — отрицание дизъюнкции, УИ — удаление импликации, ОИ — отрицание импликации, ВЭ — введение эквивалентности,УЭ — удаление эквивалентности, ВО — введение (двойного) отрицания,УО — удаление (двойного) отрицания,
Пример.
Таким образом,
Пример. Докажем, что из гипотез
Таким образом,
Правила вывода второго рода:
100.
Пример.
Пусть требуется обосновать выводимость
Таким образом: 1.
Пусть переменная Аозначает высказывание «Я сдам экзамен по логике», В-«Декан доволен мной», С – «Мама накормит меня прекрасным ужином», D- «На меня обратят внимание девушки», E – «Любимая футбольная команда выиграла матч». (A É (B É C)) ├ (B É (A É C))
Переведите на естественный язык следующие формулы логики высказываний. Если Я СДАМ ЭКЗАМЕН ПО ЛОГИКЕ, и, если ДЕКАН будет ДОВОЛЕН МНОЙ, то МАМА НАКОРМИТ МЕНЯ ПРЕКРАСНЫМ УЖИНОМ ├Если ДЕКАН оказался ДОВОЛЕН МНОй и если Я СДАЛ ЭКЗАМЕН ПО ЛОГИКЕ, то МАМА НАКОРМИла МЕНЯ ПРЕКРАСНЫМ УЖИНОМ)
Если я сдам экзамен по логике, то мир перевернется, или если мир перевернется, то я сдам экзамен по логике» = (A É B) Ú (B É A)
«Он обязательно полюбит меня, но навряд ли это произойдет, если он узнает о всех моих похождениях». = А & Ø (B É A) “Я сдам экзамен по логике, если и только если не буду пропускать занятия и научусь решать задачи» = A « (ØB & С)
«Нечто утверждается либо отвергается; третьего не дано» = (А Ú Ø A) «Нельзя нечто утверждать и отвергать одновременно» = Ø (A & Ø A)
Правила введения и удаления дизъюнкции (В.Д.), (У.Д.):
Правила удаления импликации (У.И.): Правила введения и удаления эквивалентности (В.Э.), (У.Э.):
Правила введения и удаления двойного отрицания (В.О.), (У.О.): Основные непрямые правила Правила введения импликации (В.И.) и сведения к абсурду (С.А.): Производные правила Правило условного силлогизма Правило «modus tоllens»:
Правило отрицания дизъюнкции (О.Д.): Правило отрицания конъюнкции (О.К.)
Первое правило контрапозиции:
2 Правило контрапозиции:
Правило сложной контрапозиции: Правило простой конструктивной дилеммы(П.К.Д.) Правило сложной конструктивной дилеммы (С.К.Д.)
Правило простой деструктивной дилеммы (П.Д.Д.)
Правило сложной деструктивной дилеммы (С.Д.Д.)
|



 7.
7.  8.
8.  9. УК1: 10. ВД2: 11. ОД: 12. ОИ: 13. УЭ2: 14.
9. УК1: 10. ВД2: 11. ОД: 12. ОИ: 13. УЭ2: 14.  15.
15.  16.
16.  17. УК2: 18. УД1: 19. УИ1: 20. ВЭ: 21. ВО: 22. ОК: 23. УО:
17. УК2: 18. УД1: 19. УИ1: 20. ВЭ: 21. ВО: 22. ОК: 23. УО: ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5. 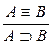 ; 6.
; 6.  ; 7.
; 7.  ; 8.
; 8. 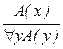 ; 9.
; 9. 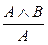 ; 10.
; 10.  ; 11.
; 11.  ; 12.
; 12.  ; 13.
; 13.  ; 16.
; 16.  ; 17.
; 17.  ; 18.
; 18.  ; 19.
; 19.  ; 20.
; 20.  ; 21.
; 21.  ; 22.
; 22.  ; 23.
; 23.  ;
;
 — отрицание квантора общности,
— отрицание квантора общности,  — отрицание квантора существования,
— отрицание квантора существования,  — введение квантора общности,
— введение квантора общности,  — удаление квантора существования,
— удаление квантора существования,  — введение квантора существования,
— введение квантора существования,  — удаление квантора общности.
— удаление квантора общности. .
.


 ,
,  , p выводима формула q.
, p выводима формула q. по определению вывода на основе (1)-(3).
по определению вывода на основе (1)-(3). ;
; .
. ;
; ,
,  .
. ;
; ;
;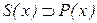




 ;
;
 ;
;
 ;
;
 ;
;

 .
. по определению вывода на основе (1)-(13); х отмечена (выводимость обоснована не полностью, т.к. безотносительность отмеченная переменная имеет свободное вхождение
по определению вывода на основе (1)-(13); х отмечена (выводимость обоснована не полностью, т.к. безотносительность отмеченная переменная имеет свободное вхождение