 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Расчетно-графическая работа
Задание 1. «Проверка статистических гипотез» Из двух нормально распределенных генеральных совокупностей 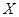 и и  получены малые независимые выборки, объемы которых получены малые независимые выборки, объемы которых 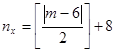 и и  , ,
где [ ] означают целую часть числа, заключенного в эти скобки,  - порядковый номер фамилии студента в групповом журнале. - порядковый номер фамилии студента в групповом журнале. Значения вариант  и и  рассчитываются по формулам: рассчитываются по формулам:  , ,  и и  , ,  , ,
где 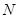 – номер студенческой группы. – номер студенческой группы. Требуется по данным выборкам при уровне значимости 0,05 проверить нулевую гипотезу  при альтернативной гипотезе при альтернативной гипотезе  . . Пример вычисления для студента с параметрами 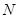 =0, =0,  =1. =1. Решение. Определим объемы выборок:  = =  = =  =[2,5]+8=2+8=10 =[2,5]+8=2+8=10
 = =  = =  =[3]+7=3+7=10. =[3]+7=3+7=10.
Далее найдем значения вариант обеих выборок: x1=1+5,5=6,5; x2=7,5; x3=8,5; x4=9,5; x5=10,5; x6=11,5; x7=12,5; x8=13,5; x9=14,5; x10=15,5; y1=  =2; y2=3; y3=4; y4=5; y5=6; y6=7; y7=8; y8=9; y9=10; y10=11. =2; y2=3; y3=4; y4=5; y5=6; y6=7; y7=8; y8=9; y9=10; y10=11. Вычислим средние и исправленные дисперсии:  =11; =11;
 = =  ·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)= ·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)=  · 41,25= · 41,25=  · 13,756≈9,167, · 13,756≈9,167,
 =6,5; =6,5;
 = =  ·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)=9,167. ·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)=9,167.
Проверим сначала гипотезу о равенстве дисперсий  , при конкурирующей , при конкурирующей  . .  , ,  , так как , так как   , то гипотеза о равенстве дисперсий принимается. , то гипотеза о равенстве дисперсий принимается.
Можно переходить к сравнению математических ожиданий.  , ,  (0,05,18)=2,10, так как (0,05,18)=2,10, так как  то гипотеза то гипотеза  о равенстве математических ожиданий отвергается. о равенстве математических ожиданий отвергается.
Задание 2. «Оценивание параметров и проверка гипотезы о нормальном законе распределения» По выборочным данным, представленным ниже, требуется проверить гипотезу о нормальном законе распределения по критериям согласия Пирсона и критерию Колмогорова на уровне значимости 0,05. Здесь 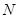 - номер студенческой группы, - номер студенческой группы,  - номер фамилии студента в журнале. - номер фамилии студента в журнале. | 11,70 | 12,90 | 10,32 | 9,50 | 5,91 | 11,56 | 10,81 | 9,32 | 13,00 | 12,90 | | 7,35 | 11,80 | 17,00+  /10 /10 | 14,10 | 9,74 | 9,76 | 6,96 | 15,05 | 14,67 | 9,73+N/10 | | 11,35 | 10,51 | 15,95 | 12,41 | 13,56 | 6,68 | 13,75 | 16,95 | 8,81 | 10,60+N/10 | | 13,90 | 9,03 | 7,39 | 13,85 | 11,99 | 6,23 | 12,56 | 12,03 | 12,97 | 15,95 | | 11,00 | 7,76 | 10,48 | 12,80 | 12,05 | 12,33 | 5,60-  /10 /10 | 8,80 | 9,85 | 10,11+  /10 /10 | | 9,75 | 13,70 | 12,09 | 13,40 | 9,02 | 6,67 | 12,37 | 11,67 | 12,00 | 13,60 | | 15,21 | 9,70 | 13,70 | 16,10 | 13,60 | 14,40 | 14,75 | 8,06 | 13,01 | 10,70+N/10 | | 13,57 | 15,30 | 12,30 | 15,85 | 17,60 | 11,25 | 12,75 | 11,50 | 12,27 | 11,50 | | 9,21 | 10,79 | 11,11 | 12,31 | 16,80 | 16,20 | 10,36 | 6,86 | 12,90 | 8,64+(N+  )/10 )/10 | | 14,90 | 16,00 | 12,00 | 12,31 | 9,35 | 16,60 | 15,67 | 15,33 | 8,69+  /10 /10 | 12,07 | Пример вычисления для студента с параметрами 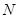 =0, =0,  =0. =0. Решение. | 11,70 | 12,90 | 10,32 | 9,50 | 5,91 | 11,56 | 10,81 | 9,32 | 13,00 | 12,90 | | 7,35 | 11,80 | 17,00 | 14,10 | 9,74 | 9,76 | 6,96 | 15,05 | 14,67 | 9,73 | | 11,35 | 10,51 | 15,95 | 12,41 | 13,56 | 6,68 | 13,75 | 16,95 | 8,81 | 10,60 | | 13,90 | 9,03 | 7,39 | 13,85 | 11,99 | 6,23 | 12,56 | 12,03 | 12,97 | 15,95 | | 11,00 | 7,76 | 10,48 | 12,80 | 12,05 | 12,33 | 5,60 | 8,80 | 9,85 | 10,11 | | 9,75 | 13,70 | 12,09 | 13,40 | 9,02 | 6,67 | 12,37 | 11,67 | 12,00 | 13,60 | | 15,21 | 9,70 | 13,70 | 16,10 | 13,60 | 14,40 | 14,75 | 8,06 | 13,01 | 10,70 | | 13,57 | 15,30 | 12,30 | 15,85 | 17,60 | 11,25 | 12,75 | 11,50 | 12,27 | 11,50 | | 9,21 | 10,79 | 11,11 | 12,31 | 16,80 | 16,20 | 10,36 | 6,86 | 12,90 | 8,64 | | 14,90 | 16,00 | 12,00 | 12,31 | 9,35 | 16,60 | 15,67 | 15,33 | 8,69 | 12,07 | Для удобства расположим варианты в порядке возрастания. | 5,60 | 8,06 | 9,50 | 10,48 | 11,50 | 12,05 | 12,56 | 13,56 | 14,40 | 15,95 | | 5,91 | 8,64 | 9,70 | 10,51 | 11,50 | 12,07 | 12,75 | 13,57 | 14,67 | 15,95 | | 6,23 | 8,69 | 9,73 | 10,60 | 11,56 | 12,09 | 12,80 | 13,60 | 14,75 | 16,00 | | 6,67 | 8,80 | 9,74 | 10,70 | 11,67 | 12,27 | 12,90 | 13,60 | 14,90 | 16,10 | | 6,68 | 8,81 | 9,75 | 10,79 | 11,70 | 12,30 | 12,90 | 13,70 | 15,05 | 16,20 | | 6,86 | 9,02 | 9,76 | 10,81 | 11,80 | 12,31 | 12,90 | 13,70 | 15,21 | 16,60 | | 6,96 | 9,03 | 9,85 | 11,00 | 11,99 | 12,31 | 12,97 | 13,75 | 15,30 | 16,80 | | 7,35 | 9,21 | 10,11 | 11,11 | 12,00 | 12,33 | 13,00 | 13,85 | 15,33 | 16,95 | | 7,39 | 9,32 | 10,32 | 11,25 | 12,00 | 12,37 | 13,01 | 13,90 | 15,67 | 17,00 | | 7,76 | 9,35 | 10,36 | 11,35 | 12,03 | 12,41 | 13,40 | 14,10 | 15,85 | 17,60 | 1) находим размах выборки:
 , ,
2) определяем число классов разбиения по формуле Стерджесса:  , ,
3) находим величину классового интервала:  , ,
4) границы и середины частичных интервалов находим по формулам: 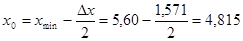 , ,
 , ,
 и так далее, и так далее,
 , ,
 и так далее. и так далее.
5) подсчитываем частоты попадания вариант в каждый интервал: | Границы интервалов | Середина интервала | Эмпирическая частота |  |  |  |  | | 4,815 | 6,385 | 5,600 | | | 6,385 | 7,956 | 7,171 | | | 7,956 | 9,527 | 8,741 | | | 9,527 | 11,097 | 10,312 | | | 11,097 | 12,668 | 11,883 | | | 12,668 | 14,239 | 13,453 | | | 14,239 | 15,809 | 15,024 | | | 15,809 | 17,380 | 16,595 | | | 17,380 | 18,951 | 18,165 | | Эмпирический интервальный ряд составлен, найдём среднее значение и СКО:  , ,  . .
Теперь найдём теоретические частоты, предполагая нормальное распределение совокупности: | Границы интервалов |  |  | Границы интервалов |  |  |   - - - -  |  |  |  |  | 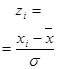 | | 4,815 | 6,385 | - | -5,497 |  | -1,921 | -0,5 | -0,4726 | 0,0274 | 2,74 | | 6,385 | 7,956 | -5,497 | -3,927 | -1,921 | -1,372 | -0,4726 | -0,4147 | 0,0579 | 5,79 | | 7,956 | 9,527 | -3,927 | -2,356 | -1,372 | -0,823 | -0,4147 | -0,2939 | 0,1208 | 12,08 | | 9,527 | 11,097 | -2,356 | -0,785 | -0,823 | -0,274 | -0,2939 | -0,1064 | 0,1875 | 18,75 | | 11,097 | 12,668 | -0,785 | 0,785 | -0,274 | 0,274 | -0,1064 | 0,1064 | 0,2128 | 21,28 | | 12,668 | 14,239 | 0,785 | 2,356 | 0,274 | 0,823 | 0,1064 | 0,2939 | 0,1875 | 18,75 | | 14,239 | 15,809 | 2,356 | 3,923 | 0,823 | 1,372 | 0,2939 | 0,4147 | 0,1208 | 12,08 | | 15,809 | 17,380 | 3,923 | 5,497 | 1,372 | 1,921 | 0,4147 | 0,4726 | 0,0579 | 5,79 | | 17,380 | 18,951 | 5,497 | - | 1,921 |  | 0,4726 | 0,5 | 0,0274 | 2,74 |  | | | Найдём наблюдаемые значения  и и  . .  |  |  |  |  |  |  |  | | 2,74 | 0,03 | 0,0274 | 0,03 | 0,0274 | 0,0026 | 0,0247 | | 5,79 | 0,07 | 0,0579 | 0,10 | 0,0853 | 0,0147 | 0,2529 | | 12,08 | 0,11 | 0,1208 | 0,21 | 0,2061 | 0,0039 | 0,0966 | | 18,75 | 0,16 | 0,1875 | 0,37 | 0,3936 | 0,0236 | 0,4033 | | 21,28 | 0,24 | 0,2128 | 0,61 | 0,6064 | 0,0036 | 0,3477 | | 18,75 | 0,19 | 0,1875 | 0,80 | 0,7939 | 0,0061 | 0,0033 | | 12,08 | 0,09 | 0,1208 | 0,89 | 0,9147 | 0,0247 | 0,7853 | | 5,79 | 0,10 | 0,0579 | 0,99 | 0,9726 | 0,0174 | 3,0612 | | 2,74 | 0,01 | 0,0274 | 1,00 | 1,00 | | 1,1050 | | |  = =0,0247 = =0,0247  =0,247 =0,247 |   = =6,080 = =6,080 | Критические значения находим в соответствующих таблицах: 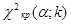 = =  , так как , так как  6,08< 6,08< 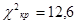 , то принимается гипотеза о нормальном распределении генеральной совокупности, аналогично , то принимается гипотеза о нормальном распределении генеральной совокупности, аналогично
 , так как , так как  < <  , то гипотеза о нормальном законе распределения подтверждается и критерием Колмогорова. , то гипотеза о нормальном законе распределения подтверждается и критерием Колмогорова.
Доказали, что совокупность распределена нормально, найдём оценки генеральных параметров этой совокупности.   |    |    |    | | -6,283 | 118,428 | -744,083 | 4675,073 | | -4,712 | 155,421 | -732,344 | 3450,805 | | -3,142 | 108,59 | -341,19 | 1072,019 | | -1,571 | 39,489 | -62,037 | 97,46 | | | | | | 1,57 | 46,833 | 73,528 | 115,439 | | 3,141 | 88,793 | 278,899 | 876,022 | | 4,172 | 222,029 | 1046,201 | 4929,699 | | 6,282 | 39,476 | 247,988 | 1557,861 |  | 8,19 | -2,33 | 167,744 |  |  |  | 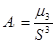 |  |  |  | | 11,883 | 8,274 | 2,876 | -0,0979 | -0,548 | 12,064 | 11,948 | Найдём доверительный интервал для математического ожидания  при неизвестной дисперсии при неизвестной дисперсии  . .  , где , где 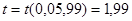 , ,  , ,

Найдём доверительный интервал для дисперсии  при неизвестном при неизвестном  . .  , где , где  , ,  , ,
 , ,
 , ,
 . .
|

 , где
, где 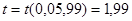 ,
, 


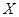 и
и  получены малые независимые выборки, объемы которых
получены малые независимые выборки, объемы которых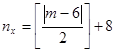 и
и  ,
, - порядковый номер фамилии студента в групповом журнале.
- порядковый номер фамилии студента в групповом журнале. и
и  рассчитываются по формулам:
рассчитываются по формулам: ,
,  и
и  ,
,  ,
,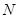 – номер студенческой группы.
– номер студенческой группы. при альтернативной гипотезе
при альтернативной гипотезе  .
. =
=  =
=  =[2,5]+8=2+8=10
=[2,5]+8=2+8=10 =
=  =
=  =[3]+7=3+7=10.
=[3]+7=3+7=10. =2; y2=3; y3=4; y4=5; y5=6; y6=7; y7=8; y8=9; y9=10; y10=11.
=2; y2=3; y3=4; y4=5; y5=6; y6=7; y7=8; y8=9; y9=10; y10=11. =11;
=11; =
=  ·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)=
·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)=  · 41,25=
· 41,25=  · 13,756≈9,167,
· 13,756≈9,167, =6,5;
=6,5; =
=  , при конкурирующей
, при конкурирующей  .
. ,
,  , так как
, так как 
 , то гипотеза о равенстве дисперсий принимается.
, то гипотеза о равенстве дисперсий принимается. ,
,  (0,05,18)=2,10, так как
(0,05,18)=2,10, так как  то гипотеза
то гипотеза  ,
, ,
, ,
,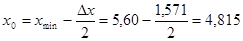 ,
, ,
, и так далее,
и так далее, ,
, и так далее.
и так далее.


 ,
,  .
.






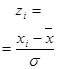



 и
и  .
.





 = =0,0247
= =0,0247  =0,247
=0,247
 = =6,080
= =6,080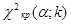 =
=  , так как
, так как 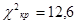 , то принимается гипотеза о нормальном распределении генеральной совокупности, аналогично
, то принимается гипотеза о нормальном распределении генеральной совокупности, аналогично , так как
, так как  <
<  , то гипотеза о нормальном законе распределения подтверждается и критерием Колмогорова.
, то гипотеза о нормальном законе распределения подтверждается и критерием Колмогорова.







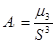



 при неизвестной дисперсии
при неизвестной дисперсии  .
. ,
,
 , где
, где  ,
,  ,
, ,
, ,
, .
.