 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Тема №2«Нахождение точечных и интервальных оценок параметров распределения»
Цель:научиться определять точечные и интервальные статистические оценки генеральных параметров нормального распределения по выборочным данным генеральной совокупности. Краткие теоретические сведения: Статистической оценкой(статистикой) неизвестного параметра qраспределения генеральной совокупности называют функцию результатов наблюдений q* Статистическая оценка q* является случайной величиной. Оценка, определяемая одним числом, зависящим от выборочных данных, называется точечной. Требования, предъявляемые к точечным статистическим оценкам: 1) состоятельность (стремление по вероятности к оцениваемому параметру при 2) несмещённость (отсутствие систематических ошибок при любом объёме выборки 3) эффективность (среди всех возможных оценок эффективная оценка обладает наименьшей дисперсией). Точечные оценки генеральных параметров нормально распределённой совокупности:
Интервальной оценкой называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надёжность точечной оценки. Точностью Предельной ошибкой выборки Надёжностью (доверительной вероятностью) оценки q* называют вероятность Вероятность того, что неизвестный параметр не попадёт в интервал |q-q*|< Доверительным называется интервал (q*- Интервальные оценки параметров нормального распределения: 1) Доверительный интервал для математического ожидания
2) Доверительный интервал для математического ожидания
 , где , где  находят из таблицы коэффициентов Стьюдента. находят из таблицы коэффициентов Стьюдента. 3) Доверительный интервал для дисперсии
4) Доверительный интервал для дисперсии
Пример 1. Вычислить несмещённые оценки параметров генеральной совокупности Решение.
Пример 2. Найти доверительные интервалы для математического ожидания, дисперсии и стандартного отклонения при уровне значимости 0,05, если из генеральной совокупности сделана выборка, используемая в примере 1. Решение. Используем данные из примера 1 для нахождения доверительного интервала для математического ожидания при неизвестной дисперсии:
где
Используем данные из примера 1 для нахождения доверительного интервала для дисперсии при неизвестном математическом ожидании:
где
Контрольные вопросы: 1. Статистическая оценка неизвестного параметра теоретического распределения. 2. Точечная оценка. 3. Требования к точечным оценкам: несмещённость, состоятельность, эффективность. 4. Генеральная и выборочная средняя. 5. Генеральная и выборочная дисперсии. 6. Поправочный коэффициент. Исправленная выборочная дисперсия. 7. Генеральное среднеквадратическое отклонение и его точечная оценка. 8. Оценка дисперсии и СКО выборочной средней. 9. Интервальная оценка неизвестного параметра генеральной совокупности. 10. Доверительная вероятность и уровень значимости. 11. Доверительный интервал. 12. Правило нахождения доверительного интервала. 13. Доверительный интервал для математического ожидания 14. Доверительный интервал для математического ожидания 15. Доверительный интервал для дисперсии 16. Доверительный интервал для дисперсии Контрольные задания: 1. При проверке успеваемости факультета были выборочно протестированы 50 обучаемых, распределившихся по результатам тестирования следующим образом (
Найти средний балл. 2. Некто N собрал следующий статистический материал, касающийся дистанции при его общении с другими людьми в течение недели:
Найти выборочную среднюю дистанции общения. 3. Найти разброс среднего балла в задании 1 тестирования 50 студентов. 4. Найти оценку разброса скорости чтения, распределение, которой представлено в таблице, предварительно определив относительную частоту средней скорости чтения.
5. Найти несмещённые оценки генеральной средней, дисперсии и среднеквадратического отклонения генеральной совокупности по выборке объема 12: 289, 208, 259, 243, 232, 210, 251, 246, 224, 239, 220, 211. 6. Имеется выборка объема: 127, 124, 155, 129, 77, 147, 65, 109, 145, 141. Определить дисперсию и среднеквадратическое отклонение выборочной средней. 7. Для исследования доходов населения города, составляющего 20 тыс. человек, по схеме собственно-случайной бесповторной выборки было отобрано 1000 жителей. Результаты приведены в таблице:
а) вероятность того, что средний месячный доход жителя города отличается от среднего дохода его в выборке не более чем на 45 у.е.; б) границы, в которых с вероятностью 8. Случайная величина 9. Количественный признак 10. Для 9 претендентов на должность руководителя была проведена оценка профессионального показателя Задания для домашней работы: 1. Найти оценки генеральных средней, дисперсии и среднего квадратического отклонения, если совокупность задана таблицей распределения:
2. Вычислить несмещённые оценки параметров генеральной совокупности 71 71 69 74 75 70 78 66 69 74 81 73 74 3. Из генеральной совокупности извлечена выборка объема
Оценить с надежностью 0,95 математическое ожидание нормально распределённого признака генеральной совокупности с помощью доверительного интервала. 4. Найти доверительные интервалы для математического ожидания, дисперсии и среднего квадратического отклонения при доверительной вероятности 0,95, если из генеральной совокупности сделана выборка: 67 70 69 68 74 72 66 66 74 69 72 78 67
Тема №3 «Проверка статистических гипотез» Цель:научиться проверять статистические гипотезы о равенстве дисперсий и математических ожиданий нормальных генеральных совокупностей, научиться применять критерий
Краткие теоретические сведения: Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений. Нулевой (основной) называют выдвинутую гипотезу Конкурирующей (альтернативной) называют гипотезу Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Вероятность совершить ошибку второго рода – уровень значимости Статистическим критерием называют случайную величину Наблюдаемым значением Критической областью называют совокупность значений критерия, при которой нулевую гипотезу отвергают. Область принятия гипотезы – совокупность значений критерия, при котором гипотезу принимают. Если Критическими точками Критические точки ищут, исходя из требования, что при условии справедливости нулевой гипотезы, вероятность того, что критерий Для каждого критерия имеются соответствующие таблицы, по которым находят критическую точку, удовлетворяющую этому требованию. Когда Сравнение двух дисперсий нормальных генеральных совокупностей: Пусть 1) выдвигаем конкурирующую гипотезу 2) находим 3) по таблице критических точек Фишера – Снедекора находим 4) если Сравнение двух математических ожиданий нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы: Пусть 1) выдвигаем конкурирующую гипотезу 2) находим 3) находим 4) если Если закон распределения генеральной совокупности неизвестен, то соответствующие критерии, используемые для установления этого закона, называются непараметрическими. Дисперсионный анализ применяют, чтобы установить, оказывает ли существенное влияние некоторый качественный фактор Идея дисперсионного анализа состоит в сравнении «факторной дисперсии», порожденной воздействием фактора, и «остаточной дисперсии», обусловленной случайными причинами. Если различия между дисперсиями значимо, то фактор оказывает существенное влияние на Пусть на Результаты наблюдений оформляются в виде таблицы:
Далее рассчитываем остаточную и факторную дисперсии по формулам:
Гипотеза о значимости фактора принимается, если Пример. Произведено 10 испытаний, из них 4 на первом уровне фактора, 4 – на втором и 2 – на третьем.
Методом дисперсионного анализа при уровне значимости 0,01 проверить нулевую гипотезу о равенстве математических ожиданий. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями. Решение.
44942-40960=3982,
=44272-40960=3312,
Qост=3982-3312=670.
S2факт=
Так как Fнабл>Fкр – нулевую гипотезу о равенстве математических ожиданий отвергаем, следовательно, принимаем гипотезу о значимости фактора.
Критерий согласия Пирсона служит для проверки гипотезы о предполагаемом законе распределения. Сравнивается эмпирическое распределение с теоретическим, но возможно и сравнение двух эмпирических распределений. 1) выдвигаем гипотезу о том, что данное эмпирическое распределение подчиняется конкретному закону, 2) находим то есть определяем меру расхождения эмпирических и теоретических частот, 3) для выбранного уровня значимости по таблице 4) если Критерий Колмогорова: Имеет то же назначение что и критерий Пирсона. 1) выдвигаем гипотезу о том, что данное эмпирическое распределение подчиняется конкретному закону, 2) строим эмпирическую функцию распределения 3) находим 4) по таблице критических точек для данного уровня значимости находим 5) если Критерий Колмогорова – Смирнова: Служит для проверки гипотез об однородности выборки – то есть гипотез о том, что рассматриваемые выборки извлечены из одной о той же генеральной совокупности. Сравниваются две эмпирические функции распределения. 1) выдвигаем гипотезу о том, что выборки однородны, 2) находим 3) при 4) если
Контрольные вопросы: 1. Понятие статистической гипотезы. 2. Нулевая и конкурирующая гипотезы. 3. Ошибки 1-го и 2-го рода. 4. Понятие статистического критерия. Наблюдаемое значение критерия. 5. Критическая область, область принятия гипотезы. Критические точки. 6. Основной принцип проверки нулевой гипотезы. 7. Статистический критерий для проверки гипотезы 8. Статистический критерий для проверки гипотезы 9. Понятие о дисперсионном анализе. 10. Назначение 11. Наблюдаемое и критическое значения критерия Пирсона. 12. Алгоритм сравнения эмпирического распределения с теоретическим с помощью критерия Пирсона. 13. Назначение 14. Наблюдаемое и критическое значения критерия Колмогорова. 15. Алгоритм сравнения эмпирического распределения с теоретическим с помощью критерия Колмогорова. 16. Назначение 17. Наблюдаемое и критическое значения критерия Колмогорова - Смирнова. 18. Алгоритм сравнения двух эмпирических распределений с помощью критерия Колмогорова. Контрольные задания: 1. По двум независимым выборкам объёмов 2. По двум независимым малым выборкам, объёмы которых соответственно равны 3. Имеются следующие данные о числе сданных экзаменов в сессию студентами-заочниками:
На уровне значимости 0,05 проверить гипотезу о том, что случайная величина Х – число сданных студентами экзаменов – распределена по биномиальному закону, используя критерий Пирсона. 4. Имеются следующие данные о засоренности партии семян клевера семенами сорняков:
На уровне значимости 0,05 проверить гипотезу о том, что случайная величина Х – число семян сорняков – распределена по закону Пуассона, используя критерий Пирсона. 5. В выборке из здоровых лиц мужского пола, студентов технических и военно-технических вузов в возрасте от 19 до 22 лет, средний возраст 20 лет, проводился тест Люшера в 8 -цветном варианте. Установлено, что жёлтый цвет предпочитается испытуемыми чаще, чем отвергается. Можно ли утверждать, что распределение жёлтого цвета по 8 позициям у здоровых испытуемых отличается от равномерного распределения? Экспериментальные данные наблюдаемых частот попадания жёлтого цвета на каждую из восьми позиций представлены в таблице.
Задания для домашней работы: 1. По двум выборкам при уровне значимости 0,05 проверить сначала гипотезу о равенстве дисперсий и, если она принимается, то затем гипотезу о равенстве математических ожиданий: 73 69 66 74 72 76 75 72 72 64 68 73 68 68 69 71 60 80 72 72 69 69 75 72 71 69 2. Используя критерий Пирсона, при уровне значимости 0,05 установить, случайно или значимо расхождение между эмпирическими частотами
|



 .
.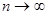 ),
), (q*) = q),
(q*) = q),
 - выборочная средняя
- выборочная средняя
 - исправленная дисперсия
- исправленная дисперсия
 - исправленное среднеквадратическое отклонение
- исправленное среднеквадратическое отклонение

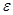 оценки называется отклонение по модулю q* от q.
оценки называется отклонение по модулю q* от q. называется максимально допустимое по модулю отклонение q* от q.
называется максимально допустимое по модулю отклонение q* от q.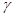 , с которой осуществляется неравенство |q-q*|<
, с которой осуществляется неравенство |q-q*|<  - уровню значимости.
- уровню значимости. , где
, где  находят из таблицы функции Лапласа, учитывая
находят из таблицы функции Лапласа, учитывая  .
. <
<  , где
, где  - находят из таблицы распределения
- находят из таблицы распределения  при 1-
при 1-  ,
,  - находят при
- находят при  .
. , где
, где  .
. по выборочным данным: 64 63 71 68 73 71 74 73 70 75 68 67 73.
по выборочным данным: 64 63 71 68 73 71 74 73 70 75 68 67 73. ,
, ,
, ,
, .
. ,
,
 .
.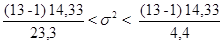 ,
, =
=  (
(  )=
)=  =4,4 и
=4,4 и  =
= 
 .
. - балл,
- балл,  - количество обучаемых с данным баллом):
- количество обучаемых с данным баллом): заключен средний месячный доход, в) объём выборки, для которой те же доверительные границы имели бы место с доверительной вероятностью 0,9973.
заключен средний месячный доход, в) объём выборки, для которой те же доверительные границы имели бы место с доверительной вероятностью 0,9973.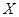 имеет нормальное распределение с известным средним квадратическим отклонением
имеет нормальное распределение с известным средним квадратическим отклонением  =24,5, если объём выборки
=24,5, если объём выборки  и задана надёжность оценки
и задана надёжность оценки  .
. найдены выборочная средняя
найдены выборочная средняя  . Оценить неизвестное математическое ожидание при помощи доверительного интервала с надёжностью 0,95.
. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надёжностью 0,95. , характеризующего способность руководить людьми. Считая показатель
, характеризующего способность руководить людьми. Считая показатель  усл. ед., определить с надёжностью
усл. ед., определить с надёжностью  доверительный интервал для истинного среднего квадратического отклонения
доверительный интервал для истинного среднего квадратического отклонения 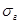 показателя
показателя  по выборочным данным. По желанию можно составить вариационный ряд по значениям:
по выборочным данным. По желанию можно составить вариационный ряд по значениям: :
: - критерий Колмогорова,
- критерий Колмогорова,  - критерий Колмогорова – Смирнова, для сравнения эмпирического распределения с теоретическим.
- критерий Колмогорова – Смирнова, для сравнения эмпирического распределения с теоретическим. .
.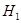 , которая противоречит нулевой.
, которая противоречит нулевой. .
. , которая служит для проверки нулевой гипотезы.
, которая служит для проверки нулевой гипотезы. называют значение критерия, вычисленное по выборкам.
называют значение критерия, вычисленное по выборкам. называют точки, отделяющие критическую область от области принятия гипотезы.
называют точки, отделяющие критическую область от области принятия гипотезы. <
<  ,
,  распространены нормально. По независимым выборкам с объемами, соответственно равными
распространены нормально. По независимым выборкам с объемами, соответственно равными  , извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии
, извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии  и
и  . Требуется по исправленным дисперсиям при заданном уровне значимости
. Требуется по исправленным дисперсиям при заданном уровне значимости  .
. (
(  ),
), ,
, (
(  ), где
), где  ,
,  и
и  - объём выборки, которой соответствует
- объём выборки, которой соответствует  ,
,  -
-  ,
, , то принимаем нулевую гипотезу, в противном случае – альтернативную.
, то принимаем нулевую гипотезу, в противном случае – альтернативную. и
и  и исправленные дисперсии
и исправленные дисперсии  , то есть значимо или незначимо различаются средние. Предполагаем (если есть основание) дисперсии одинаковы или сравниваем их.
, то есть значимо или незначимо различаются средние. Предполагаем (если есть основание) дисперсии одинаковы или сравниваем их. (
(  ), [
), [  ],
],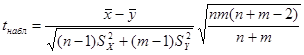 ,
, по таблице критических точек Стьюдента и симметричную ей
по таблице критических точек Стьюдента и симметричную ей  ,
, (
(  ), [
), [  ], то принимаем нулевую гипотезу.
], то принимаем нулевую гипотезу. , который имеет
, который имеет  уровней
уровней  на изучаемую величину
на изучаемую величину  . Тогда наблюдалось
. Тогда наблюдалось  признака
признака  – номер испытания,
– номер испытания,  – номер уровня фактора.
– номер уровня фактора.





 …
… 

 …
… 

 …
… 
 ,
, ,
,  ,
, ,
,  .
. , где
, где  и отвергается, если
и отвергается, если  (смотрите сравнение двух дисперсий нормальных генеральных совокупностей).
(смотрите сравнение двух дисперсий нормальных генеральных совокупностей).

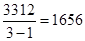 , S2ост=
, S2ост=  .
. ,
, 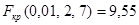 .
.
 , где
, где 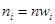 и
и  - эмпирические и теоретические частоты,
- эмпирические и теоретические частоты,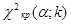 , где
, где  ,
,  - число параметров теоретического распределения,
- число параметров теоретического распределения, <
<  , то частоты расходятся незначительно, а, следовательно, нет оснований отвергать нулевую гипотезу.
, то частоты расходятся незначительно, а, следовательно, нет оснований отвергать нулевую гипотезу. и предполагаемую теоретическую
и предполагаемую теоретическую  ,
, , где
, где  ,
, ,
, , то принимаем нулевую гипотезу.
, то принимаем нулевую гипотезу. , где
, где  - эмпирические функции распределения, построенные по двум выборкам объемов
- эмпирические функции распределения, построенные по двум выборкам объемов  и
и  ,
, находим в специальных таблицах, при
находим в специальных таблицах, при 
 совпадает со статистикой Колмогорова
совпадает со статистикой Колмогорова  <
<  , то принимаем нулевую гипотезу, то есть выборки однородны.
, то принимаем нулевую гипотезу, то есть выборки однородны.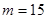 , извлечённым из нормальных генеральных совокупностей
, извлечённым из нормальных генеральных совокупностей  и
и  , извлечённым из нормальных генеральных совокупностей
, извлечённым из нормальных генеральных совокупностей  ,
, 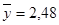 и исправленные дисперсии
и исправленные дисперсии  и
и  При уровне значимости 0,05 проверить нулевую гипотезу
При уровне значимости 0,05 проверить нулевую гипотезу