 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Пример решение задачи №2: Построение и исследование эконометрической модели магазина в виде линейной троичной регрессии
Постановка задачи №2
Торговая компания располагает семью магазинами типа«Промтовары»(для справки: этот тип в соответствии с /2, ГОСТ/ -предприятие розничной торговли, реализующее непродовольственные товары узкого ассортимента, основные из которых швейные и трикотажные изделия, обувь, галантерея, парфюмерия торговой площадью от 18 м2). Компании планирует построить 8-й магазин с торговой площадью 1100 м2, для чего она разрабатывает бизнес-план и, в частности, эконометрическую модель магазина. На этой модели специалисты должны исследовать зависимость объема продаж (у - в десятках тыс.руб./день) от размера торговой площади (х1 – в сотнях м2) и от размера паркинга (х2 в десятках автомашин) Единицы измерения выбраны с учетом достоверности данных и удобства вычислений.
Решение задачи №2
1) Нанести в координатах х2у точки на плоскость (построить корреляционное поле). Решение. Для наглядности выберем наши данные из таблиц 1.2-1.7. Из рисунке 3.1 видно, что прямая линия хорошо аппроксимирует связь между у и х2. Эта связь прямая и очень тесная. 2) Записать для своего варианта матрицу Х значений объясняющих переменных (матрицу плана). Решение. См.среднюю матрицу в п. 4. 3) Записать транспонированную матрицу плана Решение. См. левую матрицу в п. 4.
Рисунок 3.1
2.4. Найти произведение матриц Решение.
5) Найти обратную матрицу ( Решение. Для краткости введем обозначение: А=
где
Находим алгебраические дополнения:
Обратная матрица:
Проверка. Если расчеты верны, то должно выполниться равенство: А А-1 = Е. Для повышения точности множитель 1/192 введем отдельно.
Равенство выполнено, значит, расчет обратной матрицы выполнен верно.
6) Найти произведение матриц Решение.
7) Найти уравнение регрессии Y по Х1 и Х2 в форме Решение.
Итак, ответ: b0 = -0,88; b1 = 0,50; b2 = 1,63. Уравнение множественной регрессии имеет вид: 8) Объяснить смысл изменения значения коэффициента регрессии b1. Решение. В задаче №1 значение b1=1,54, а теперь его значение снизилось до b1=0,50. Это связано с тем, что на объем продаж помимо торговой площади теперь влияет учитываемая площадь паркинга. 9) Рассчитать значения коэффициентов эластичности для обоих факторов и сравнить влияние каждого из них на средний объем продаж. Решение. Коэффициент эластичности в общем случае есть функция объясняющей переменной, например: Если 10) Оценить аналитически прогнозное среднее значение объема продаж для проектируемого магазина "СИ" с торговой площадью х1=11 (1100 м2) и паркинговой площадью х2 = 8 (80 автомашин). Решение. Объем продаж рассчитаем по уравнению регрессии:
11.а) Найти 95%-ный доверительный интервал для среднего прогнозного значения объема продаж магазина "СИ". Решение. По условию нужно оценить значение Мх(Y), где вектор переменных
Для удобства вычислений составим таблицу 3.1. Таблица 3.1
На основе табличных данных:
По табл. П2 находим критическое значение статистики Стьюдента t0,95; 7-2-1=5 = 2,78. Полуинтервал D = t0,95; 5∙ Нижняя граница интервала: Верхняя граница интервала:
11.б) Найти 95%-ный доверительный интервал для индивидуального прогнозного значения объема продаж магазина "СИ" Решение. Интервал рассчитаем по выражению:
где Полуинтервал D = 2,78 × 1,82 = 5,06. Нижние и верхние границы интервала:
12) Проверить значимость коэффициентов регрессии. Решение. Стандартная ошибка рассчитывается по формуле:
где выражение под корнем есть диагональный элемент матрицы Отсюда: sb1 = 1,09 Так как t = çb1ç/ sb1 = 0,50/1,28 = 0,39 < t0,95;4 = 2,78, то коэффициент b1 незначим (незначимо отличается от нуля). Так как t = çb2ç/ sb2 = 1,63/0,83 = 1,96 < t0,95;4 = 2,78, то и коэффициент b2 незначим на 5%-ном уровне. 13) Найти с надежностью 0,95 интервальные оценки коэффициентов регрессии b1 и b2 и дисперсии s2. Решение. Интервалы коэффициентов регрессии рассчитываются по формуле: bj + t1-a,n-p-1sbj £ bj £ bj + t1-a,n-p-1sbj.
Поскольку оба коэффициента регрессии незначимы, то не имеет смысла строить для них доверительные интервалы. 14) Определить множественный коэффициент детерминации и проверить значимость уравнения регрессии на уровне a=0,05. Решение. Коэффициент детерминации рассчитывается по формуле:
Уравнение регрессии значимо, если справедливо неравенство (критерий Фишера): F = R2 (n-p-1)/(1- R2) p > Fa;k1;k2.
Отсюда F = 0,96(7-2-1)/(1-0,962)2 = 24,62 > F0,05;2;4. Вывод: уравнение значимо. 15) Определить, существенно ли увеличилось значение коэффициента детерминации при введении в регрессию второй объясняющей переменной. Решение. Значения коэффициентов детерминации для регрессий с одной и с двумя объясняющими переменными соответственно равны: R2 = 0,97 и R2 = 0,96. Увеличения значения не произошло. Введение второй переменной не увеличило адекватность модели.
|



 .
. .
.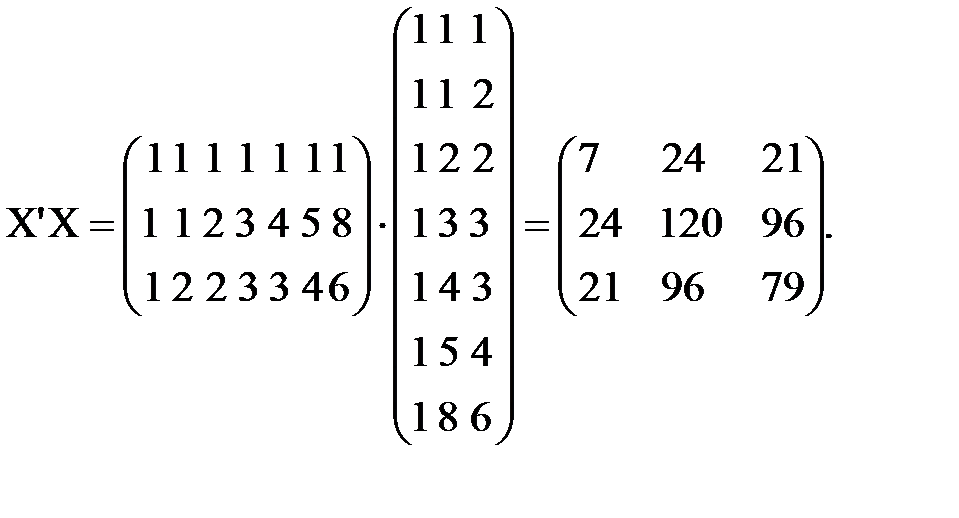
 )-1.
)-1. . требуется найти обратную матрицу А-1. Используем формулу:
. требуется найти обратную матрицу А-1. Используем формулу:
 - определитель матрицы А,
- определитель матрицы А, – транспонированная матрица, составленная из алгебраических дополнений матрицы А.
– транспонированная матрица, составленная из алгебраических дополнений матрицы А.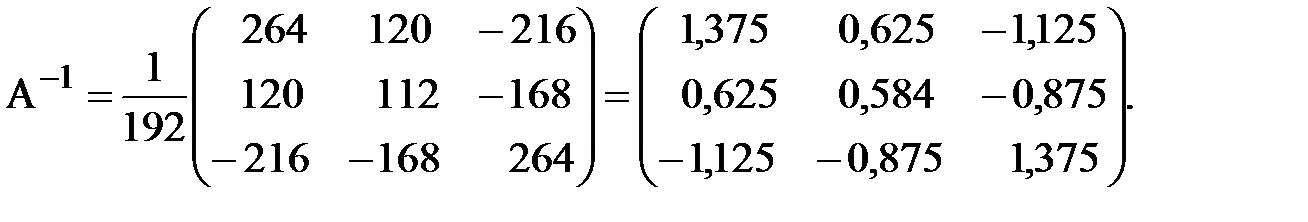

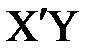 .
.
 =b0+ b1 х1 + + b2х2 методом наименьших квадратов путем умножения матрицы (
=b0+ b1 х1 + + b2х2 методом наименьших квадратов путем умножения матрицы ( 


 то
то  при увеличении х1 от среднего на 1% объем продаж возрастет на 0,30%. Аналогично
при увеличении х1 от среднего на 1% объем продаж возрастет на 0,30%. Аналогично  при увеличении х2 от среднего на 1% объем продаж возрастет на 0,86%.
при увеличении х2 от среднего на 1% объем продаж возрастет на 0,86%. . Выборочной оценкой условного МO Мх(Y) является значение регрессии
. Выборочной оценкой условного МO Мх(Y) является значение регрессии  и дисперсию возмущений s2:
и дисперсию возмущений s2: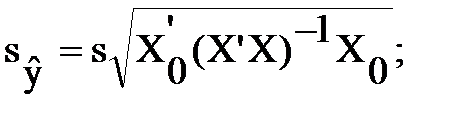


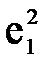




 = 2,78 × 1,46 = 4,05.
= 2,78 × 1,46 = 4,05. .
.


 -1.
-1. = 1,28; sb2 =1,09
= 1,28; sb2 =1,09  = 0,83.
= 0,83.


 ;
; 
