ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Пример решения задачи №1: Построение и исследование эконометрической модели магазина в виде линейной парной регрессии
Эконометрика Методические указания и задания по выполнению контрольной работы для обучающихся в магистратуре по направлениям 38.04.01 Экономика, 38.04.08 Финансы и кредит
Калининград, 2015
Рецензент
А.Н. Кохан, к.э.н. доцент кафедры финансов и кредита ФГБОУ ВПО «КГТУ»
Методические указания рассмотрены и одобрены на заседании кафедры финансов и кредита ФГБОУ ВПО «КГТУ», протокол № 2 от 30.09.2015 г. Содержание
1 Общие сведения, выбор варианта и исходных данных
Контрольная работа состоит из введения, 5-ти разделов: (задача-1, задача-2, зада-3, вопрос-1, вопрос-2) и списка использованных источников. Объём работы вместе с титульным листом, листом «Содержание», списком использованных источников не должен превышать 18 страниц. Поскольку студентам будет доступен электронный вариант настоящих указаний, то свой текст они могут создавать на основе данного текста (примеров решения задач), вставляя свои исходные данные, вычисления и выводы по пунктам расчёта. Это значительно снизит трудоёмкость выполнения контрольной работы. Для защиты работы процесс решения должен быть хорошо осмыслен. Во введении рекомендуем отразить историю становления эконометрики, её особенности как научной дисциплины (1-2 стр). Работа оформляется в точном соответствии с правилами, изложенными в /1, см форум/, список использованных источников оформляется по правилам, изложенным на сайте КГТУ в разделе Библиотека. Вариант работы выбирается по первым подходящим буквам полного имени и фамилии. Таблица 1.1 - Варианты и номера теоретических вопросов
*первая подходящая буква полного имени Теоретические вопросы 1) Эконометрическая модель зависимости потребления домохозяйства от дохода (4 алгебраических выражения - модель Торнквиста) 2) Основные понятия ТВ и МС: случайная величина, дифференциальный и интегральный законы распределения СВ, нормальный ЗР СВ, регрессия 3) Основные понятия ТВ и МС: математическое ожидание, дисперсия и СКО, парный коэффициент корреляции, генеральная и выборочные совокупности 4) Основные понятия математики: производные простых функций, исследование функций, асимптота, правило Лопиталя, транспонирование и перемножение матриц, обращение матрицы, единичная матрица, определитель 3-го порядка, минор и алгебраическое дополнение 5) Метод наименьших квадратов - на примере парной регрессии (вывести формулы для коэффициентов b0 и b1) 6) Пять предпосылок для НКЛРМ (в том числе смысл понятий гомо- и гетероскедастичности) 7) Точечные оценки параметров - три критерия качества оценивания: несмещённость, состоятельность, эффективность 8) Две интервальные оценки прогноза суточной выручки магазина (на примере исследований из задачи №1 контрольной работы) 9) Оценка значимости уравнения регрессии: по F-критерию Фишера, по коэффициентам детерминации: простому и скорректированному (на примерах задач №1 и №2) 10) Мультиколлинеарность и отбор значимых факторов (как пример использовать переменные Х и Х1, Х2 из 1-й и 2-й задач контрольной работы, для отбора в качестве критериев использовать остаточную дисперсию и скорректированный коэффициент детерминации) 11) Линейные регрессионные модели с атрибутивными переменными (на примере торгового предприятия) 12) Эластичность регрессии - функция и коэффициент, формула для построения и их смысл (на примере регрессий из 1-й и 2-й задач контрольной работы) 13) Классификация нелинейных регрессионных моделей; пример линеаризации модели нелинейной по переменным, но линейной по параметрам 14) Классификация нелинейных регрессионных моделей; пример линеаризации модели нелинейной по параметрам, но внутренне линейной 15) Критерий однородности выборки Чоу 16) Производственная функция Кобба-Дугласа, её смысл и линеаризация; числовой пример для 3-х предприятий 17) Частные коэффициенты корреляции, элиминированные переменные (на примере задачи №2 контрольной работы) 18) Структура и классификация временных рядов, автокорреляционная функция 19) Авторегрессионные модели и модели скользящих средних 20) Эконометрические проблемы, связанные с оцениванием гедонических уравнений цен /14, Берндт, с. / Исходные данные для задач 1, 2 и 3 выбираются по одной из таблиц 1.2-1.6. Например, вы – Ольга Иванова, значит ваша таблица 1.5. Во второй графе таблицы выбирается столбец – выделен жирным - со значениями переменной Х (кв.м). По первой подходящей букве вашей фамилии выбирается столбец со значениями для переменной Y (руб/сутки). Для Ольги Ивановой это – столбец В (её вариант - ОВ) - выделен курсивом. В таблице 1.7 приведены дополнительные данные для задачи 2. Соответствующий столбец выбирается по 1-й подходящей букве имени, для Ольги столбец выделен курсивом. Таблица 1.2 - Исходные данные для задач 1 и 2, первая подходящая буква имени А
Таблица 1.3 - Исходные данные для задач 1 и 2, первая подходящая буква имени Е
Таблица 1.4 - Исходные данные для задач 1 и 2, первая подходящая буква имени И
Таблица 1.5 - Исходные данные для задач 1 и 2, первая подходящая буква имени О
Таблица 1.6 - Исходные данные для задач 1 и 2, первая подходящая буква имени Я
Таблица 1.7 - Исходные дополнительные данные для задачи 2
Постановки задач и ход их решения у всех студентов одинаковые. Ниже приведены примеры решения задач, логике которых можно следовать «буква в букву». Пример решения задачи №1: Построение и исследование эконометрической модели магазина в виде линейной парной регрессии
Постановка задачи №1
Торговая компания располагает семью магазинами типа «Товары повседневного спроса»(для справки: этот тип в соответствии с /2, ГОСТ/ - предприятие розничной торговли, реализующее продовольственные и непродовольственные товары частого спроса, преимущественно по форме самообслуживания, с торговой площадью от 100 м2).
Компании планирует построить 8-й магазин с торговой площадью 1100 м2, для чего она разрабатывает бизнес-план и, в частности, эконометрическую модель магазина. На это модели специалисты должны исследовать зависимость объема продаж (у - в десятках тыс.руб./день) от размера торговой площади (х – в сотнях м2). Единицы измерения выбраны с учетом достоверности данных и удобства вычислений.
Решение задачи №1
1) Нанести в координатах ХY точки на плоскость (построить корреляционное поле). Решение. Для наглядности выберем наши данные из таблицы 1.2: Таблица 2.1
На рисунке 2.1 представлено корреляционное поле. Как видно, оно должно хорошо аппроксимироваться прямой линией. Зависимость между Х и Y тесная и прямая. 2) Найти методом наименьших квадратов уравнение регрессии Y по Х в линейной форме:
Решение. Расчетные формулы для неизвестных параметров регрессии:
На основе таблицы 2.1 рассчитаем необходимые суммы, входящие в формулу (2.2).
Рисунок 2.1
Таблица 2.2
Искомые оценки параметров регрессии и само уравнение регрессии:
3) Построить линию регрессии на координатной плоскости XY. Решение. Искомую линию проще всего построить по двум точкам (см. рис. 2.1), например (0; 0,43) и (8,00; 12,75). 4) Показать графически и аналитически, что линия регрессии проходит через точку ( Решение. Из графика на рисунке 2.1 видно, что линия регрессии проходит через точку “средних” ( 5) На сколько вырастет средний объем продаж при увеличении х на 1. Решение. При увеличении торговой площади на 1 (100 м2) в среднем объем продаж увеличится на b1= 1,54 (т.е. на 15400 руб./день). 6) Имеет ли смысл свободный член в уравнении регрессии. Решение. Свободный член b0=0,43 смысла не имеет, т.к. при нулевой торговой площади положительного объема продаж быть не может. 7) Вычислить коэффициент корреляции между переменными X и Y. Решение. Используем формулу:
Здесь известно все, кроме
Окончательно Полученное значение коэффициента корреляции говорит о высокой (почти функциональной) зависимости объема продаж от размера торговой площади.
8) Определить графически и аналитически прогнозное среднее значение объема продаж для проектируемого магазина "СИ" с торговой площадью х=11 (напомним, что это 1100 м2). Решение. Прогнозное значение из рисунка 2.1 и из формулы совпадают:
9.а) Найти 95%-ный доверительный интервал для среднего прогнозного значения объема продаж. Решение. Оценка значения условного МО Мх=11(Y) равна 17,37. Чтобы построить доверительный интервал для СВ Для этого определим дисперсию возмущений (см. табл. 2.2 графы 4-6):
Искомая дисперсия
Для статистики Стьюдента
Нижнее значение интервала: 17,37-2,57×1,48=13,57. Верхнее значение интервала: 17,37+2,57×1,48=21,37. Окончательно интервал имеет вид:
9.б) Найти 95%-ный доверительный интервал для индивидуального прогнозного значения объема продаж Решение. Чтобы построить доверительный интервал для СВ
Нижнее значение интервала: 17,37-2,57×1,88=12,54. Верхнее значение интервала: 17,37+2,57×1,88=22,20. Окончательно интервал имеет вид:
12,54 £
Как и следует из теории, этот интервал больше предыдущего и большой по величине. Коэффициент осцилляции для него:
Ко=(R/
1.10. а) Найти с надежностью 0,95 интервальные оценки коэффициента регрессии b1. Решение. Общая формула для расчета интервала: b1-D £ b1 £ b1+D, где Нижнее значение интервала: 1,54-0,48=1,06. Верхнее значение интервала: 1,54+0,48=2,02. Окончательно интервал имеет вид: 1,06 £ b1 £ 2,02.
10а) Найти с надежностью 0,95 интервальные оценки коэффициента регрессии b1. Решение. Общая формула для расчета интервала: b1-D £ b1 £ b1+D,
где Нижнее значение интервала: 1,54-0,48=1,06. Верхнее значение интервала: 1,54+0,48=2,02. Окончательно интервал имеет вид: 1,06 £ b1 £ 2,02.
10.б) Найти с надежностью 0,95 интервальные оценки дисперсии возмущений s2. Решение. Найдем по табл.П3 (критерий Пирсона) табличное значение статистики хи-квадрат: Формула для доверительного интервала:
11а) Оценить на уровне a=0,05 значимость уравнения регрессии Y по Х по критерию Фишера. Решение. Вычислим суммы квадратов. Общая сумма: Q=å(yi- Регрессионная сумма: QR=å( Остаточная сумма: Qe=å( Значение статистики Фишера :
Уравнение регрессии значимо, если F > Fa,k1,k2, где степени свободы k1=m-1=2-1=1, k2=n-m=7-2=5. По табл. П4 находим критическое значение F0,05;1;5=6,61. Так как 69,66 > 6,61, то уравнение значимо: коэффициент регрессии b1 =1,54 значимо отличается от нуля. 11б) Оценить на уровне a=0,05 значимость уравнения регрессии Y по Х по критерию Стьюдента. Решение. Уравнение парной регрессии значимо, если t>tкрит. Значение статистики Стьюдента:
По табл. П2 находим tкрит.=t0,95;7-2=5=2,57. Так как 8,22 > 2,57, то гипотезу Но(Но : β1=0) отвергаем и принимаем противоположную гипотезу Н1: уравнение значимо. 12) Определить коэффициент детерминации R2 и раскрыть его смысл: на сколько процентов в среднем объем продаж зависит от размера торговой площади. Решение. Используем формулу: R2= QR/Q = 92,16 / 95,47 = 0,97. R2 показывает, какая доля вариации зависимой переменной обусловлена вариацией объясняющей переменной. Ответ: эта доля составляет 97%.
|



 =b0+ b1x.
=b0+ b1x.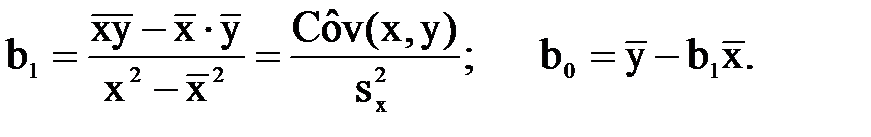 (2.2)
(2.2) )2
)2 xi
xi xi-yi)2
xi-yi)2



 ,
, 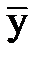 ).
). (2.4)
(2.4)



 =0,43+1,54×11=17,37 (173700 руб./день)
=0,43+1,54×11=17,37 (173700 руб./день) х=11, нужно оценить дисперсию ее оценки
х=11, нужно оценить дисперсию ее оценки  .
.


 число степеней свободы k = n – 2 = 7 – 2 = 5. По табл. П2 находим значение t0,95;5=2,57 критерия Стьюдента. Искомый 95%-ный доверительный интервал для среднего прогнозного значения объема продаж магазина "СИ":
число степеней свободы k = n – 2 = 7 – 2 = 5. По табл. П2 находим значение t0,95;5=2,57 критерия Стьюдента. Искомый 95%-ный доверительный интервал для среднего прогнозного значения объема продаж магазина "СИ":


 £ 22,20.
£ 22,20. )100%= ((22,2-12,54)/17,37)100%=55,6%.
)100%= ((22,2-12,54)/17,37)100%=55,6%.





 )2=13,77+7,35+2,93+0,51+0,51+1,67+68,73= 95,47.
)2=13,77+7,35+2,93+0,51+0,51+1,67+68,73= 95,47.