 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Условия равновесия произвольной пространственной системы сил.
Произвольную пространственную систему сил, как и плоскую, можно привести к какому-нибудь центру О и заменить одной результирующей силой ΣXi = 0; ΣMx (Pi) = 0; ΣYi = 0; ΣMy (Pi) = 0; ΣZi = 0; ΣMz (Pi) = 0. Таким образом, для равновесия пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил системы на каждую из координатных осей, а также суммы моментов всех сил системы относительно каждой из этих осей равнялись нулю. В частных случаях системы сходящихся или параллельных сил эти уравнения будут линейно зависимы, и только три уравнения из шести будут линейно независимыми. Например, уравнения равновесия системы сил, параллельных оси Oz, имеют вид: ΣZi = 0; ΣMx (Pi) = 0; ΣMy (Pi) = 0.
Задачи на равновесие тела под действием пространственной системы сил. Принцип решения задач этого раздела остается тем же, что и для плоской системы сил. Установив, равновесие, какого тела будет рассматриваться, заменяют наложенные на тело связи их реакциями и составляют условия равновесия этого тела, рассматривая его как свободное. Из полученных уравнений определяются искомые величины. Для получения более простых систем уравнений рекомендуется оси проводить так, чтобы они пересекали больше неизвестных сил или были к ним перпендикулярны (если это только излишне не усложняет вычисления проекций и моментов других сил). Новым элементом в составлении уравнений является вычисление моментов сил относительно осей координат. В случаях, когда из общего чертежа трудно усмотреть, чему равен момент данной силы относительно какой-нибудь оси, рекомендуется изобразить на вспомогательном чертеже проекцию рассматриваемого тела (вместе с силой) на плоскость, перпендикулярную к этой оси. В тех случаях, когда при вычислении момента возникают затруднения в определении проекции силы на соответствующую плоскость или плеча этой проекции, рекомендуется разложить силу на две взаимно перпендикулярные составляющие (из которых одна параллельна какой-нибудь координатной оси), а затем воспользоваться теоремой Вариньона. Пример 5. Рама АВ (рис.45) удерживается в равновесии шарниром А и стержнем ВС. На краю рамы находится груз весом Р. Определим реакции шарнира и усилие в стержне.
Рис.45
Рассматриваем равновесие рамы вместе с грузом. Строим расчётную схему, изобразив раму свободным телом и показав все силы, действующие на неё: реакции связей и вес груза Р. Эти силы образуют систему сил, произвольно расположенных на плоскости. Желательно составить такие уравнения, чтобы в каждом было по одной неизвестной силе. Рекомендуется составлять уравнения моментов относительно трёх точек, точек пересечения линий действия неизвестных сил.
И, прежде чем составлять уравнения, сделаем еще одно полезное замечание. Если на расчётной схеме имеется сила, расположенная так, что плечо её находится непросто, то при определении момента рекомендуется предварительно разложить вектор этой силы на две, более удобно направленные. В данной задаче разложим силу Составляем уравнения:
Из второго уравнения находим
Из третьего
И из первого
Так как получилось S<0, то стержень ВС будет сжат. Пример 6. Прямоугольная полка весом Р удерживается в горизонтальном положении двумя стержнями СЕ и СD, прикреплёнными к стене в точке Е. Стержни одинаковой длины, AB=2a, EO=a. Определим усилия в стержнях и реакции петель А и В.
Рис.46
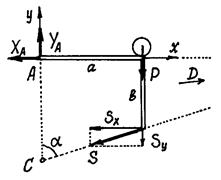
Рассматриваем равновесие плиты. Строим расчётную схему (рис.46). Реакции петель принято показывать двумя силами перпендикулярными оси петли: Силы образуют систему сил, произвольно расположенных в пространстве. Можем составить 6 уравнений. Неизвестных - тоже шесть. Какие уравнения составлять – надо подумать. Желательно такие, чтобы они были попроще и чтобы в них было поменьше неизвестных. Составим такие уравнения:
Из уравнения (1) получим: S1=S2. Тогда из (4): Из (3): YA=YB и, по (5), Из треугольника Поэтому Для проверки решения можно составить ещё одно уравнение и посмотреть, удовлетворяется ли оно при найденных значениях реакций:
Задача решена правильно. Вопросы для самопроверки - Какая конструкция называется фермой? - Назовите основные составные элементы фермы. - Какой стержень фермы называется нулевым? - Сформулируйте леммы, определяющие нулевой стержень фермы. - В чем заключается сущность способа вырезания узлов? - На основании каких соображений без вычислений можно определить стержни пространственных ферм, в которых при заданной нагрузке усилия равны нулю? - В чем заключается сущность способа Риттера? - Каково соотношение между нормальной реакцией поверхности и силой нормального давления? - Что называется силой трения? - Запишите закон Амонтона-Кулона. - Сформулируйте основной закон трения. Что такое коэффициент трения, угол трения и от чего зависит их значение? - Брус находится в равновесии, опираясь на гладкую вертикальную стену и шероховатый горизонтальный пол; центр тяжести бруса находится в его середине. Можно ли определить направление полной реакции пола? - Назовите размерность коэффициента трения скольжения. - Что такое предельная сила трения скольжения. - Что характеризует конус трения? - Назовите причину появления момента трения качения. - Какова размерность коэффициента трения качения? - Приведите примеры устройств, в которых возникает трение верчения. - В чем заключается разница между силой сцепления и силой трения? - Что называют конусом сцепления? - Каковы возможные направления реакции шероховатой поверхности? - Что представляет собой область равновесия и каковы условия равновесия сил, приложенных к бруску, опирающемуся на две шероховатые поверхности? - Что называется моментом силы относительно точки? Какова размерность этой величины? - Как вычислить модуль момента силы относительно точки? - Сформулируйте теорему о моменте равнодействующей системы сходящихся сил. - Что называется моментом силы относительно оси? - Запишите формулу, связывающую момент силы относительно точки с моментом этой же силы относительно оси, проходящей через эту точку. - Как определяется момент силы относительно оси? - Почему при определении момента силы относительно оси нужно обязательно спроецировать силу на плоскость, перпендикулярную оси? - Каким образом нужно расположить ось, чтобы момент данной силы относительно этой оси равнялся нулю? - Приведите формулы для вычисления моментов силы относительно координатных осей. - Как направлен вектор момента силы относительно относительно точки? - Как определяется на плоскости момент силы относительно точки? - Какой площадью можно определить числовое значение момента силы относительно данной точки? - Изменяется ли момент силы относительно данной точки при переносе силы вдоль линии ее действия? - В каком случае момент силы относительно данной точки равен нулю? - Определите геометрическое место точек пространства, относительно которых моменты данной силы: а) геометрически равны; б) равны по модулю. - Как определяются числовое значение и знак момента силы относительно оси? - При каких условиях момент силы относительно оси равен нулю? - При каком направлении силы, приложенной к заданной точке, ее момент относительно данной оси наибольший? - Какая зависимость существует между моментом силы относительно точки и моментом той же силы относительно оси, проходящей через эту точку? - При каких условиях модуль момента силы относительно точки равен моменту той же силы относительно оси, проходящей через эту точку? - Каковы аналитические выражения моментов силы относительно координатных осей? - Чему равны главные моменты системы сил, произвольно расположенных в пространстве, относительно точки и относительно оси, проходящей через эту точку? Какова зависимость между ними? - Чему равен главный момент системы сил, лежащих в одной плоскости, относительно любой точки этой плоскости? - Чему равен главный момент сил, составляющих пару, относительно любой точки в пространстве? - Что называется главным моментом системы сил относительно заданного полюса? - Как формулируется лемма о параллельном переносе силы? - Сформулируйте теорему о приведении произвольной системы сил к главному вектору и главному моменту. - Запишите формулы для вычисления проекций главного момента на координатные оси. - Приведите векторную запись условий равновесия произвольной системы сил. - Запишите условия равновесия произвольной системы сил в проекциях на прямоугольные координатные оси. - Сколько независимых скалярных уравнений равновесия можно записать для пространственной системы параллельных сил? - Запишите уравнения равновесия для произвольной плоской системы сил. - При каком условии три непараллельные силы, приложенные к твердому телу, уравновешиваются? - Каково условие равновесия трех параллельных сил, приложенных к твердому телу? - Каковы возможные случаи приведения произвольно расположенных и параллельных сил в пространстве? - К какому простейшему виду можно привести систему сил, если известно, что главный момент этих сил относительно различных точек пространства: а) имеет одно и то же значение не равное нулю; б) равен нулю; в) имеет различные значения и перпендикулярен главному вектору; г) имеет различные значения и неперпендикулярен главному вектору. - Каковы условия и уравнения равновесия пространственной системы сходящихся, параллельных и произвольно расположенных сил и чем они отличаются от условий и уравнений равновесия такого же вида сил на плоскости? - Какие уравнения и сколько их можно составить для уравновешенной пространственной системы сходящихся сил? - Запишите систему уравнений равновесия пространственной системы сил? - Каковы геометрические и аналитические условия приведения пространственной системы сил к равнодействующей? - Сформулируйте теорему о моменте равнодействующей пространственной системы сил относительно точки и оси. - Составьте уравнения линии действия равнодействующей. - Какую прямую в пространстве называют центральной осью системы сил? - Выведите уравнения центральной оси системы сил? - Покажите, что две скрещивающиеся силы можно привести к силовому винту. - По какой формуле вычисляют наименьший главный момент заданной системы сил? - Запишите формулы для расчета главного вектора пространственной системы сходящихся сил? - Запишите формулы для расчета главного вектора пространственной системы произвольно расположенных сил? - Запишите формулу для расчета главного момента пространственной системы сил? - Какова зависимость главного момента системы сил в пространстве от расстояния центра приведения до центральной оси этой системы сил? - Относительно каких точек пространства главные моменты заданной системы сил имеют один и тот же модуль и составляют с главным вектором один и тот же угол? - Относительно каких точек пространства главные моменты системы сил геометрически равны между собой? - Каковы инварианты системы сил? - Каким условиям удовлетворяют задаваемые силы, приложенные к твердому телу с одной и двумя закрепленными точками, находящемуся в покое? - Будет ли в равновесии плоская система сил, для которой алгебраические суммы моментов относительно трех точек, расположенных на одной прямой, равны нулю? - Пусть для плоской системы сил суммы моментов относительно двух точек равны нулю. При каких дополнительных условиях система будет в равновесии? - Сформулируйте необходимые и достаточные условия равновесия плоской системы параллельных сил. - Что такое моментная точка? - Какие уравнения (и сколько) можно составить для уравновешенной произвольной плоской системы сил? - Какие уравнения и сколько их можно составить для уравновешенной пространственной системы параллельных сил? - Какие уравнения и сколько их можно составить для уравновешенной произвольной пространственной системы сил? - Изложите рекомендации предпочтительного выбора моментных точек и объясните их. - С чего рекомендуется начинать решение задачи на равновесие системы сил? - Как формулируется план решения задач статики на равновесие сил?
|
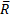и парой с моментом 
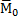. Рассуждая так, что для равновесия этой системы сил необходимо и достаточно, чтобы одновременно было R = 0 и Mо = 0. Но векторы 
В нашей задаче это точка А, где приложены неизвестные 
и 
; точка С, где пересекаются линии действия неизвестных сил 
; точка D – точка пересечения линий действия сил 
и 
и 
(рис.37) такие, что модули их 
.
.
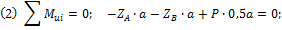
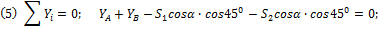
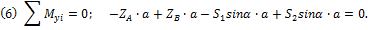
. Значит 
Из уравнения (6), т.к. S1=S2, следует ZA=ZB. Тогда по (2) ZA=ZB=P/4.
, где 
, следует 
, 
YA=YB=0,25P, ZA=ZB0,25P.
