ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Зависимость между моментами силы относительно центра и относительно оси.
Пусть на тело действует приложенная в точке А сила
Рис.42 Проведем теперь через любую точку O1 на оси z плоскость ху, перпендикулярную к оси; проектируя силу Но треугольник О1А1В1 представляет собою проекцию треугольника ОАВ на плоскость ху. Угол между плоскостями этих треугольников равен углу между перпендикулярами к плоскостям, т. е. равен Умножая обе части этого равенства на 2 и замечая, что удвоенные пощади треугольников О1А1В1 и ОАВ равны соответственно Так как произведение
В результате мы доказали, что между моментом силы относительно оси и ее моментом относительно какого-нибудь центра, лежащего на этой оси, существует следующая зависимость: момент силы
Приведение пространственной системы сил к данному центру. Полученные выше результаты позволяют решить задачу о приведении любой системы сил к данному центру. Эта задача, решается с помощью теоремы о параллельном переносе силы. Для переноса действующей на абсолютно твердое тело силы
Рис.43 Рассмотрим теперь твердое тело, на которое действует какая угодно система сил
приложенных в центре О, и система пар, моменты которых будут равны
Силы, приложенные в точке О, заменяются одной силой
Чтобы сложить все полученные пары, надо геометрически сложить векторы моментов этих пар. В результате система пар заменится одной парой, момент которой
Как и в случае плоской системы, величина
Рис.44
Таким образом мы доказали следующую теорему, любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяется одной силой Векторы Выражения для Rx, Ry, Rz нам известны. Проекции вектора Окончательно для определения проекций главного вектора
При этом главный вектор пространственной системы сил: R0 = ΣPi отличается от главного вектора плоской системы сил только наличием третьей компоненты, поэтому его модуль будет равен:
Главный момент пространственной системы сил: M0 = ΣM0(Pi) - это вектор, модуль которого находится аналогично:
где Mx , My , Mz - суммы моментов всех сил системы относительно соответствующих осей. В зависимости от значений главного вектора и главного момента, а также от их взаимного расположения возможны следующие варианты приведения пространственной системы сил: 1) R0 = 0, M0 = 0 - система сил находится в равновесии; 2) R0 = 0, M0 ≠0 - система эквивалентна паре сил с моментом, равным главному моменту системы, который в этом случае не зависит от выбора центра приведения; 3) R0 ≠0, M0 = 0 - система эквивалентна равнодействующей R, равной и эквивалентной главному вектору системы R0 , линия действия которой проходит через центр приведения: R = R0, R~R0 ; 4) R0 ≠0, M0 ≠0 и R0 ⊥ M0 - система эквивалентна равнодействующей R, равной главному вектору системы R0 , ее линия действия проходит на расстоянии d = |M0|/ R0 от центра приведения. 5) R0 ≠ 0, M0 ≠0 и главный вектор R0 неперпендикулярен главному моменту M0 - система эквивалентна скрещивающимся силам или динаме. При этом скрещивающимися называются силы, которые непараллельны и не лежат в одной плоскости, а динамой называется система, состоящая из силы и пары сил, плоскость которой перпендикулярна этой силе. Динама, приложенная к твердому телу, стремится вызвать его винтовое движение, которое представляет совокупность вращательного и поступательного движений. Примечание. Для пространственной системы сил, как и для плоской, справедлива следующая Теорема Вариньона. Момент равнодействующей пространственной системы сил относительно произвольного центра (оси) равен геометрической (алгебраической) сумме моментов всех сил этой системы относительно данного центра (оси).
|



 (рис. 42). Проведем какую-нибудь ось z и возьмем на ней произвольную точку О. Момент силы
(рис. 42). Проведем какую-нибудь ось z и возьмем на ней произвольную точку О. Момент силы 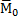 перпендикулярным плоскости ОАВ, причем по модулю
перпендикулярным плоскости ОАВ, причем по модулю  .
.
 .
. . Тогда, по известной геометрической формуле,
. Тогда, по известной геометрической формуле,  .
. и
и  .
. дает проекцию вектора
дает проекцию вектора  на ось z, то равенство можно еще представить в виде
на ось z, то равенство можно еще представить в виде или
или  .
. относительно оси равен проекции на эту ось вектора, изображающего момент данной силы относительно любого центра, лежащего на оси.
относительно оси равен проекции на эту ось вектора, изображающего момент данной силы относительно любого центра, лежащего на оси. и
и  . Тогда сила
. Тогда сила  окажется приложенной в точке О и к ней будет присоединена пара (
окажется приложенной в точке О и к ней будет присоединена пара (  ) с моментом
) с моментом 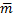 , что можно показать еще так, как на рис. 43, б. При этом
, что можно показать еще так, как на рис. 43, б. При этом  .
.
 ,
, 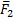 ,…,
,…,  (рис. 44, а). Выберем произвольную точку О за центр приведения и перенесем все силы системы в этот центр, присоединяя при этом соответствующие пары. Тогда на тело будет действовать система сил
(рис. 44, а). Выберем произвольную точку О за центр приведения и перенесем все силы системы в этот центр, присоединяя при этом соответствующие пары. Тогда на тело будет действовать система сил .
. ,
,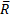 , приложенной в той же точке. При этом
, приложенной в той же точке. При этом 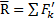 или,
или, .
. или,
или, .
. , равная геометрической сумме всех сил, называется главным вектором системы; величина
, равная геометрической сумме всех сил, называется главным вектором системы; величина  , равная геометрической сумме моментов всех сил относительно центра О, называется главным моментом системы относительно этого центра.
, равная геометрической сумме моментов всех сил относительно центра О, называется главным моментом системы относительно этого центра.
 или,
или,  . Аналогично находятся величины My и Mz.
. Аналогично находятся величины My и Mz.