 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Глава 3. Сколько узлов на отрезке?
Применение формулы Пика для вычисления площадей некоторых фигур не совсем удобно. Очень уж чётким должен быть чертёж и очень внимательно нужно его рассматривать, чтобы определить, лежит ли данный узел внутри фигуры или же попал на её границу. Как точно сосчитать число узлов на границе? Поскольку граница состоит из отрезков, то нас интересует количество узлов сетки, лежащих на произвольном отрезке с концами в узлах.
Если С отрезка АВ на расстояние А С ему треугольник С Следовательно, С что если эту процедуру продолжить, мы когда-нибудь получим в качестве очередной точки С сетки. Рассматривая большой прямоугольный треугольник ARB с гипотенузой АВ, приходим к равенствам: Рис. 1
AR = (k+1) · AD BR = (k+1) · С AB = (k+1) · A С Теперь мы можем выяснить, сколько узлов Рис. 2. лежит между точками А и В(конечно, мы считаем, что А и В не лежат на одной линии сетки). Построим прямоугольный треугольник ARB с вершинами в узлах сетки и с гипотенузой АВ (рис.2). Пусть AR = р, BR = q. Понятно, что р и q – целые положительные числа. Теорема. Если р и q взаимно просты, то между А и В на отрезке АВ нет узлов сетки. Если же наибольший общий делитель р и q равен n , где n > 1 (НОД (р, q ) = n > 1), то на отрезке АВ между точками А и В расположены ровно ( n – 1) узлов сетки. Доказательство. 1) Пусть числа p и q взаимно просты. Если между А и В были k узлов (k ≥ 1), то, взяв ближайший к А узел С 2)Пусть НОД (р,q) = n > 1. Поделив отрезки AR и BR на n равных частей, мы опять приходим к рис.1, где С Теперь, не вглядываясь долго и напряжённо в картинку и не мучаясь сомнениями, вы всегда можете сказать, через сколько узлов проходит произвольный отрезок с концами в узлах сетки! Задача 1. [11]В прямоугольнике 4×7, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала? Задача 2.В прямоугольнике размером 200×300, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала на две части?
Задачу 1 легко решить, просто «водя пальцем по картинке» Рис. 3 (рис.3). Для решения задачи 2 полезно вспомнить наши разговоры о количестве узлов на отрезке и обсуждение рис.1: ясно, что вдоль диагонали прямоугольника 200×300 можно расположить 100 прямоугольников 2×3, и в каждом из них, очевидно, диагональ будет рассекать по 4 клетки. Поэтому ответ к задаче 2 – четыреста клеток. В задаче 3 такие соображения, увы, не помогают: числа 1000 и 1003 взаимно не просты. Сформулируем эту задачу в общем виде: Сколько клеток рассекает на две части диагональ прямоугольника m×n, где m и n – взаимно простые числа?
Итак, мы получили «цепочку», идущую из левого нижнего угла в правый верхний. Нам надо понять, Рис. 4 чему равно число клеток в этой цепочке. Дадим каждой клетке адрес (t, s), если она расположена в горизонтальном ряду с номером t и вертикальном ряду с номером s. Левый нижний угол получает адрес (1,1), а правый верхний – (m,n). Теперь остаётся заметить, что при переходе от клетки с номером k в нашей цепочке к клетке с номером k+1 сумма чисел t и s в адресе возрастает точно на 1. Значит, чтобы перейти от клетки с адресом (1,1) к клетке с адресом (m,n), надо сделать ровно m + n – 2 шагов, пройдя, таким образом, m + n – 1 клеток.
Объединим задачи 2 и 3. Пусть m и n – произвольные натуральные числа. Сколько клеток рассекает диагональ прямоугольника m×n? Пусть d = НОД (m×n). Как и при решении задачи 2, мы видим, что вдоль диагонали исходного прямоугольника образуется d маленьких прямоугольников Теперь при желании мы можем без труда сосчитать, сколько клеток рассекут диагонали следующих прямоугольников: 36×56, 105×24, 2003×111.
Заключение Предметом исследования явилось применение формулы Пика при решении задач, на нахождение площади фигур, изображённых на клетчатой бумаге. При выполнении работы были решены задачи на нахождение площади многоугольников, изображённых на клетчатой бумаге различными способами: непосредственного применения формул, геометрическим и с помощью формулы Пика. Анализ решений показал, что применение формулы Пика даёт возможность решать задачи на нахождение площади многоугольника, изображённого на клетчатой бумаге быстро и легко. Это позволяет экономить время на ЕГЭ по математике. Эта работа вызвала у нас интерес, и мы надеемся, что наши выводы, полученные в результате наших исследований, помогут выпускникам одиннадцатых классов при сдаче ЕГЭ по математике.В результате нашей работы мы расширили свои знания о решении задач на клетчатой бумаге, определили для себя классификацию исследуемых задач, убедились в их многообразии. Мы научились вычислять площади многоугольников, нарисованных на клетчатом листке, встретились с совсем новыми, необычными «расстояниями», узнали, как раскраска клеточек помогает решать многие задачи. Рассмотренные нами задания имеют различный уровень трудности – от простых до олимпиадных. Каждый может найти среди них задачи посильного уровня сложности, отталкиваясь от которых, можно будет переходить к решению более трудных. Работа по данной теме позволила нам преодолеть психологический барьер и поверить в свои силы, что является важнейшим фактором успешного решения олимпиадных и экзаменационных задач, выступления перед аудиторией с теоретическим материалом по математике. Мы пришли к выводу, что тема, которая нас заинтересовала, достаточно многогранна, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны.
Список используемой литературы 1. Болотин И. Б., Добрышина Л. Ф. Смоленские математические олимпиады школьников (готовимся к ЕГЭ). Смол. гос. ун-т; Смоленск: СмолГУ, 2008. 2.Васильев Н.Б. Вокруг формулы Пика, журнал «Квант» №12,1974 г., с.39-43. 3. Геометрия на клетчатой бумаге. Малый МЕХмат МГУ. Режим доступа: http://mmmf.msu.ru/archive/20082009/KanunnikovKuznetsov/2.html 4. Григорьева Г. И . Подготовка школьников к олимпиадам по математике: 5 – 6 классы. Метод. пособие. – М.: Глобус, 2009. 5. Дынкин Е. Б., Молчанов С. А., Розенталь А. Л . Математические соревнования. Арифметика и алгебра. – М.: Наука, 1970. 6. Жарковская Н. М., Рисс Е. А . Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25 7. Задачи открытого банка заданий по математике ФИПИ, 2010 – 2011. Режим доступа: http://mathege.ru/or/ege/ShowProblems.html?posMask=32 8. Игнатьев Е. И . В царстве смекалки. – М.: Наука, 1982.9. Кенгуру – 2010. Задачи, решения, итоги. Режим доступа: http://russian-kenguru.ru/load 9. Прасолов В. В . Задачи по планиметрии. – М.: МЦНМО, 2000. 11. Рисс Е. А . Математический клуб «Кенгуру» Выпуск № 8 (изд. второе). – Санкт-Петербург, 2009. 12. Смирнова И. М., Смирнов В. А . Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009. 13. Смирнова И. М., Смирнов В. А . Геометрические задачи с практическим содержанием. – М.: Чистые пруды, 2010. 14. Смирнов В. А. ЕГЭ. Математика. Задача В6. Планиметрия. Р/т. – М.: МЦНМО, 2011. 15. Трошин В. В. Занимательные дидактические материалы по математике. Сборник заданий. Выпуск 2. – М.: Глобус, 2008. 16. Гарднер М. Математические чудеса и тайны. – М.: Наука, 1986. 17. Задачи открытого банка заданий по математике ФИПИ, 2010 – 2011. Режим доступа:http://mathege.ru/or/ege/ShowProblems.html?posMask=32
|



 Сделаем сначала небольшое наблюдение. Пусть А и В – узлы сетки. Обозначим через С
Сделаем сначала небольшое наблюдение. Пусть А и В – узлы сетки. Обозначим через С  первый узел, встречавшиеся после А на отрезке АВ (значит, между А и С
первый узел, встречавшиеся после А на отрезке АВ (значит, между А и С  D
D  точку В – узел
точку В – узел
 – целое число, большее, чем n (поскольку
– целое число, большее, чем n (поскольку  ). Но если мы воспользуемся формулой (1), то увидим, что р = AR = (k+1) · AD¢
). Но если мы воспользуемся формулой (1), то увидим, что р = AR = (k+1) · AD¢ 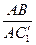 , а D¢
, а D¢  Задача 3.В прямоугольнике 1000×1003, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала?
Задача 3.В прямоугольнике 1000×1003, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала? Заметим, что диагональ такого прямоугольника не проходит через узлы. Будем считать, что диагональ идёт из левого нижнего угла прямоугольника. Самой первой она рассекает левую нижнюю угловую клетку (клетку № 1), потом она попадёт в клетку № 2 (рис.4), и так далее. Пусть диагональ уже пересекла k клеток. Так как она ни разу не проходит через узел, то всегда можно однозначно указать, какую клетку она рассечёт после клетки с номером k.
Заметим, что диагональ такого прямоугольника не проходит через узлы. Будем считать, что диагональ идёт из левого нижнего угла прямоугольника. Самой первой она рассекает левую нижнюю угловую клетку (клетку № 1), потом она попадёт в клетку № 2 (рис.4), и так далее. Пусть диагональ уже пересекла k клеток. Так как она ни разу не проходит через узел, то всегда можно однозначно указать, какую клетку она рассечёт после клетки с номером k. Итак, ответ к задаче 3 – число клеток равно 2002.
Итак, ответ к задаче 3 – число клеток равно 2002. ´
´  . Стороны этих маленьких прямоугольников уже взаимно просты, поэтому их диагонали рассекают по
. Стороны этих маленьких прямоугольников уже взаимно просты, поэтому их диагонали рассекают по  +
+  – 1 клеток каждая. Значит, диагональ исходного прямоугольника рассечёт (
– 1 клеток каждая. Значит, диагональ исходного прямоугольника рассечёт (