 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Лекция 4 Механические колебания и волны в упругих средах.
План 1. Гармонические механические колебания. Дифференциальное уравнение затухающих колебаний и его решение. 2. Уравнение бегущей волны. Длина волны и волновое число. Волновое уравнение. Когерентность. Тезисы 1. Из произвольной точки О, выбранной на оси х, под углом j, равным начальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания (рис. 199). Если этот вектор привести во вращение с угловой скоростью w0, то проекция конца вектора будет перемещаться по оси х и принимать значения от -A до +А, а колеблющаяся величина будет изменяться со временем по закону
Дифференциальное уравнение свободных затухающих колебаний линейной системы Если A(t) и A(t+T)— амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение Промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации Для пружинного маятника дифференциальное уравнение вынужденных колебаний 2. Плоская волна: колебания носят гармонический характер, а ось х совпадает с направлением распространения волны. В данном случае волновые поверхности перпендикулярны оси х, смещение x будет зависеть только от х и t, т. е. x = x(х, t). Уравнение бегущей волны есть не только периодическая функция времени, но и периодическая функция координаты Тогда уравнение плоской волны можно записать еще и в виде Скорость распространения волны есть скорость перемещения фазы волны, ее называют фазовой скоростью Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных |






 , где s — колеблющаяся величина, описывающая тот или иной физический процесс, d = const — коэффициент затухания, w0 — циклическая частота свободных незатухающихколебаний той же колебательной системы, т. е. при d=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение этого уравнения
, где s — колеблющаяся величина, описывающая тот или иной физический процесс, d = const — коэффициент затухания, w0 — циклическая частота свободных незатухающихколебаний той же колебательной системы, т. е. при d=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение этого уравнения  , где
, где  - амплитуда затухающих колебаний с периодом
- амплитуда затухающих колебаний с периодом 
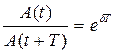 называется декрементом затухания, а его логарифм
называется декрементом затухания, а его логарифм  - логарифмическим декрементом затухания; здесь Ne - число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.
- логарифмическим декрементом затухания; здесь Ne - число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина. . Добротность колебательной системы при малых значениях логарифмического декремента равна
. Добротность колебательной системы при малых значениях логарифмического декремента равна  . Добротность пропорциональна числу колебаний Ne, совершаемых системой за время релаксации. При увеличении коэффициента затухания d колебательный процесс станет апериодическим. Пружинный маятник колеблется по закону
. Добротность пропорциональна числу колебаний Ne, совершаемых системой за время релаксации. При увеличении коэффициента затухания d колебательный процесс станет апериодическим. Пружинный маятник колеблется по закону 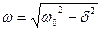 . Добротность пружинного маятника
. Добротность пружинного маятника  , где r – коэффициент сопротивления.
, где r – коэффициент сопротивления. , а его решение
, а его решение  , что соответствует линейному неоднородному дифференциальному уравнению
, что соответствует линейному неоднородному дифференциальному уравнению 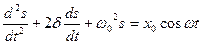
 . Если плоская волна распространяется в противоположном направлении, то в формуле будет знак +. В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид
. Если плоская волна распространяется в противоположном направлении, то в формуле будет знак +. В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид  . Для характеристики волн используется волновое число (число длин волн, укладываемых на отрезке длиной 2
. Для характеристики волн используется волновое число (число длин волн, укладываемых на отрезке длиной 2  ).
).  .
. . Уравнение волны, распространяющейся вдоль отрицательного направления оси х, будет отличаться знаком kx.
. Уравнение волны, распространяющейся вдоль отрицательного направления оси х, будет отличаться знаком kx. . Уравнение сферической волны (волны, волновые поверхности которой имеют вид концентрических сфер)
. Уравнение сферической волны (волны, волновые поверхности которой имеют вид концентрических сфер)  , где r — расстояние от центра волны до рассматриваемой точки среды.
, где r — расстояние от центра волны до рассматриваемой точки среды.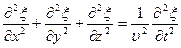 или
или 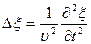 , где
, где  — фазовая скорость,
— фазовая скорость,  - оператор Лапласа. Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид
- оператор Лапласа. Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид 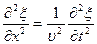 .
.