 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Теорема 1 (перше правило).
Нехай функція 1) змінює знак з «+» на «–», то при х = х0 функція має максимум; 2) змінює знак «–» на «+», то функція має у цій точці мінімум; 3) не змінює свого знака, то функція в точці х = х0 екстремуму не має. Геометрична ілюстрація теореми 1 (рис. 5). Нехай у точці х = х1 маємо
Рис. 5 Тоді при Якщо в точці х2 маємо
то при Якщо при х = х3 маємо Зауваження. На основі даної теореми можна сформулювати таке правило для дослідження неперервної функції 1. Знаходимо першу похідну функції, тобто 2. Обчислюємо критичні значення аргументу х (критичні точки), для цього: а) прирівнюємо першу похідну до нуля і знаходимо дійсні корені здобутого рівняння б) знаходимо значення х, для яких похідна 3. Досліджуємо знак похідної ліворуч і праворуч від критичної точки. Оскільки знак похідної залишається сталим в інтервалі між двома критичними точками, для дослідження знака похідної ліворуч і праворуч, наприклад від критичної точки х2, досить визначити знак похідної в точках 4. Обчислюємо значення функції Таким чином, маємо таке схематичне зображення можливих випадків: Теорема 2 (друге правило). Якщо для диференційовної функції 1) якщо друга похідна 2) якщо 3) якщо Зауваження. Для критичних точок, в яких похідна функції не існує або дорівнює нескінченності, друге правило не застосовується. 6. Найбільше і найменше значення функції на відрізку Якщо функція Найбільше значення функції на проміжку [a; b] називається абсолютним максимумом, а найменше — абсолютним мінімумом. Припустимо, що на даному проміжку функція На підставі результатів дослідження будуємо графік функції. Для точнішої побудови візьмемо додатково точки на рис. 6: (–5; – 0,3),
Рис.6 |



 неперервна на деякому інтервалі, в якому міститься критична точка х0, і диференційовна в усіх точках цього інтервалу (крім, можливо, самої точки х0). Якщо при переході зліва направо через цю точку похідна:
неперервна на деякому інтервалі, в якому міститься критична точка х0, і диференційовна в усіх точках цього інтервалу (крім, можливо, самої точки х0). Якщо при переході зліва направо через цю точку похідна: і для всіх х, достатньо близьких до точки х1, виконуються нерівності
і для всіх х, достатньо близьких до точки х1, виконуються нерівності
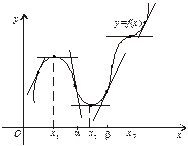
 дотична до кривої утворює з віссю Ох гострий кут — функція зростає, а при
дотична до кривої утворює з віссю Ох гострий кут — функція зростає, а при  дотична утворює з віссю Ох тупий кут — функція спадає; при х = х1 функція переходить від зростання до спадання, тобто має максимум.
дотична утворює з віссю Ох тупий кут — функція спадає; при х = х1 функція переходить від зростання до спадання, тобто має максимум. і для всіх значень х, достатньо близьких до точки х2, виконуються нерівності
і для всіх значень х, достатньо близьких до точки х2, виконуються нерівності
 дотична до кривої утворює з віссю Ох тупий кут — функція спадає, а при
дотична до кривої утворює з віссю Ох тупий кут — функція спадає, а при  дотична до кривої утворює гострий кут — функція зростає. При х = х2 функція переходить від спадання до зростання, тобто має мінімум.
дотична до кривої утворює гострий кут — функція зростає. При х = х2 функція переходить від спадання до зростання, тобто має мінімум. і для всіх значень х, достатньо близьких до х3, виконуються нерівності
і для всіх значень х, достатньо близьких до х3, виконуються нерівності  при
при  ;
;  , то функція зростає як при
, то функція зростає як при  . Звідси при х = х3 функція не має ні максимуму, ні мінімуму.
. Звідси при х = х3 функція не має ні максимуму, ні мінімуму. на максимум і мінімум.
на максимум і мінімум. .
. ;
; і
і  , де х1 і х3 — найближчі критичні точки).
, де х1 і х3 — найближчі критичні точки). у кожній критичній точці.
у кожній критичній точці. у деякій точці х0 її перша похідна
у деякій точці х0 її перша похідна  дорівнює нулю, а друга похідна
дорівнює нулю, а друга похідна  існує й відмінна від нуля, тобто
існує й відмінна від нуля, тобто  ,
,  , то:
, то: , то в точці х0 функція
, то в точці х0 функція  — максимум;
— максимум; — питання залишається відкритим, і для його розв’язання треба застосувати перше правило.
— питання залишається відкритим, і для його розв’язання треба застосувати перше правило. , (2; 3), (3; 1,3).
, (2; 3), (3; 1,3).