 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Перетворення невизначеностей виду
ЛЕКЦІЯ 8. Застосування похідної ПЛАН 1. Правило Лопіталя 2. Перетворення невизначеностей виду 3. Зростання та спадання функцій 4. Екстремуми функцій 5. Найбільше і найменше значення функції на відрізку Правило Лопіталя Розглянемо відношення
У цьому випадку, використовуючи похідні Теорема (правило Лопіталя). Границя відношення двох нескінченно малих або нескінченно великих функцій дорівнює границі відношення їхніх похідних (скінченній або нескінченній), якщо остання існує. Зауваження. Якщо
і т. п. Приклад. Знайти Виконавши граничний перехід, дістанемо невизначеність вигляду
Приклад. Знайти Виконання граничного переходу приводить до невизначеності виду
(виконання граничного переходу знову приводить до невизначеності виду
Перетворення невизначеностей виду
Правило Лопіталя можна застосувати тільки для розкриття невизначеностей вигляду Невизначеність виду Потрібно знайти
Це невизначеність типу Якщо вираз
то при Приклад. Знайти Тут маємо невизначеність вигляду
Невизначеність вигляду При а) б) в) Ці невизначеності за допомогою логарифмування зводяться до невизначеності вигляду Легко перевірити, що при Відповідно до пункту 1 розкриємо невизначеність Звідси Приклад. Знайти границю Це невизначеність виду
Обчислимо границю логарифма даної функції. Тут маємо невизначеність
Звідси Приклад. Знайти границю При
Звідси Невизначеність Приклад. Знайти границю Маємо невизначеність виду
|



 , де функції
, де функції  і
і  визначені й диференційовні в деякому околі точки а, виключаючи, можливо, саму точку а. Може бути, що при
визначені й диференційовні в деякому околі точки а, виключаючи, можливо, саму точку а. Може бути, що при  обидві функції
обидві функції  .
. і
і  , можна сформулювати правило для знаходження границі функції f (x) при
, можна сформулювати правило для знаходження границі функції f (x) при 
 .
. . Застосовуємо правило Лопіталя:
. Застосовуємо правило Лопіталя: .
. .
. . Застосовуємо правило Лопіталя:
. Застосовуємо правило Лопіталя:
 .
. до виду
до виду  . Нехай
. Нехай  .
. .
. або
або  ,
, .
. . Зобразимо добуток функції у вигляді частки, а потім, отримавши невизначеність
. Зобразимо добуток функції у вигляді частки, а потім, отримавши невизначеність 
 . Нехай маємо функцію
. Нехай маємо функцію  .
. (а — скінченне або нескінченне) можливі три випадки:
(а — скінченне або нескінченне) можливі три випадки: маємо невизначеність виду
маємо невизначеність виду  ;
; дістанемо невизначеність
дістанемо невизначеність 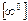 ;
; маємо невизначеність виду
маємо невизначеність виду  .
. . Прологарифмувавши цю рівність, дістанемо
. Прологарифмувавши цю рівність, дістанемо  .
. добуток
добуток  буде невизначеністю
буде невизначеністю  , тобто знайдемо границю
, тобто знайдемо границю  (k — скінченне або ¥).
(k — скінченне або ¥). .
. .
.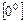 . Позначимо функцію, що стоїть під знаком границі, через у, тобто
. Позначимо функцію, що стоїть під знаком границі, через у, тобто  , і прологарифмуємо її:
, і прологарифмуємо її: .
. .
. .
. .
. маємо невизначеність
маємо невизначеність  .
. .
. .
. . Якщо функції
. Якщо функції  при
при  при
при  . Остання з допомогою алгебраїчних перетворень зводиться до невизначеності
. Остання з допомогою алгебраїчних перетворень зводиться до невизначеності  .
.
