 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Зростання та спадання функцій
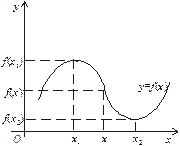
Нагадаємо: функція f (x) називається зростаючою на проміжку, якщо більшому значенню аргументу відповідає більше значення функції (якщо Теорема 1 (необхідна умова зростання (спадання) функції): 1. Якщо диференційовна функція зростає на деякому проміжку, то похідна цієї функції невід’ємна на цьому проміжку. 2. Якщо диференційовна функція спадає на деякому проміжку, то похідна цієї функції недодатна на цьому проміжку. Теорема 2 (достатня умова зростання (спадання) функції): Якщо похідна диференційовної функції додатна всередині деякого проміжку, то функція зростає на цьому проміжку. Якщо похідна диференційовної функції від’ємна всередині проміжку, то функція спадає на цьому проміжку. Приклад. Знайти проміжки зростання та спадання функції Область визначення функції — уся числова вісь Для визначення проміжку зростання функції розв’яжемо нерівність При визначенні проміжку спадання функції (рис. 4.8) маємо 8 – 2х < 0, тобто Екстремуми функцій Означення. При значенні х1 аргументу х функція f (х) має максимум f (х1), якщо в деякому околі точки х1 виконується нерівність (рис. 1)
Рис. 1 Максимум або мінімум функції називається екстремумом функції, а ті значення аргументу, при яких досягаються екстремуми функції, називаються точками екстремуму функції (відповідно точками максимуму або мінімуму функції). Екстремум функції, у загальному випадку, має локальний характер — це найбільше або найменше значення функції порівняно з ближніми її значеннями. Необхідна умова екстремуму функції. Теорема. У точці екстремуму диференційовної функції похідна її дорівнює нулю:
Геометрична умова
Рис. 2 Наслідок. Неперервна функція може мати екстремум тільки в тих точках, де похідна функції дорівнює нулю або не існує.
Справді, якщо в точці х0 екстремуму функції Те, що в точці екстремуму неперервної функції похідна може не існувати, показує приклад функції, графік якої має форму «ламаної» (рис. 3). Ті значення аргументу х, які для заданої функції перетворюють на нуль її похідну Достатні умови екстремуму функції.Із того, що
Наприклад, нехай Отже, не для будь-якого критичного значення аргументу функції |



 то
то  ); функція спадна на проміжку, якщо більшому значенню аргументу відповідає менше значення функції (якщо
); функція спадна на проміжку, якщо більшому значенню аргументу відповідає менше значення функції (якщо  ).
). .
. . Знайдемо похідну
. Знайдемо похідну  . Функція диференційовна на проміжку
. Функція диференційовна на проміжку 
 , тобто функція зростає на проміжку
, тобто функція зростає на проміжку  .
. .
. . Аналогічно: при значенні х2 аргументу х функція f (х) має мінімум f (х2), якщо в деякому околі точки х2 має місце нерівність (див. рис. 4.9)
. Аналогічно: при значенні х2 аргументу х функція f (х) має мінімум f (х2), якщо в деякому околі точки х2 має місце нерівність (див. рис. 4.9)  .
.
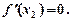
 дотична до її графіка паралельна осі Ох (рис. 2).
дотична до її графіка паралельна осі Ох (рис. 2).
 Рис. 3
Рис. 3 існує похідна
існує похідна  , то, згідно з даною теоремою, ця похідна дорівнює нулю.
, то, згідно з даною теоремою, ця похідна дорівнює нулю. або для якої похідна
або для якої похідна 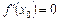 , не випливає, що функція
, не випливає, що функція  .
. Рис. 4
Рис. 4 . Тоді
. Тоді  і
і  , однак значення
, однак значення 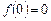 не є екстремумом даної функції, оскільки різниця
не є екстремумом даної функції, оскільки різниця  змінює знак при зміні знаку аргументу х (рис. 4).
змінює знак при зміні знаку аргументу х (рис. 4).