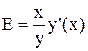ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Ценовая эластичность спроса
Глава 2 ОСНОВЫ СПРОСА И ПРЕДЛОЖЕНИЯ
Спрос Выберем рынок какого-нибудь конкретного товара и возьмем любого покупателя на этом рынке. Зафиксируем теперь цену товара. Наш покупатель за определенный промежуток времени желает и способен купить некоторое количество товара по данной цене. Это количество называют объемом (величиной) индивидуального спроса покупателя при данной цене. Объем индивидуального спроса зависит от многих факторов: цены данного товара, вкусов и предпочтений потребителя, его дохода, цен других товаров, прочих условий. Рассмотрим теперь всех покупателей в совокупности. Объем рыночного спроса есть количество товара, которое желают и способны купить все покупатели вместе в единицу времени по данной цене. Эта величина равна сумме объемов индивидуального спроса всех покупателей при данной цене. Обычно объем рыночного спроса называют для краткости просто объемом спроса. И если нет определения «индивидуальный» или «рыночный», речь идет о рыночном показателе. Ценой спроса называют максимальную цену, по которой покупатели согласны купить определенное количество данного товара. Зависимость объема спроса от цены товара называют функцией спроса, а ее график называют кривой (линией) спроса. У экономистов принято откладывать аргумент функции спроса (цену) на вертикальной оси координат, а саму эту функцию (объем спроса) — на горизонтальной оси. Функцию спроса обозначают через QJp) или D(jp) (demand — англ., спрос; price — англ., цена). Функцию спроса обычно задают аналитическим (алгебраическим), табличным или графическим способами. Если функция спроса задается аналитическим способом, то объем спроса рассчитывается путем подстановки значения цены в некоторую формулу, например: Объем спроса = 210 – 30 × Цена, или D = 210 – 30 р. При цене товара, равной трем единицам, объем спроса будет равен 120 единицам (210 – 30 × 3). При использовании аналитического способа необходимо учитывать, что если при подстановке в формулу некоторого значения цены получается отрицательное число, то объем спроса считают равным нулю. Так, в приведенном выше примере объем спроса при цене десять единиц равен нулю, поскольку подстановка этой цены в формулу дает минус 90. Цена, начиная с которой объем спроса становится равным нулю, называется максимальной ценой спроса. В нашем примере максимальная цена спроса равна семи единицам. Это значит, что даже при самом незначительном уменьшении данной цены найдутся покупатели, желающие купить некоторое количество товара по новой цене. Если функция спроса задается табличным способом, то значения цены записываются в первом столбце таблицы, а соответствующие объемы спроса — во втором ее столбце (табл. 2.1). Таблица 2.1. Табличный способ задания функции спроса
При использовании табличного способа нередко возникает проблема оценки объема спроса для цены, не указанной в таблице. Для ее решения предполагают, что в промежутках между ближайшими табличными значениями цены кривая спроса представляет собой отрезок прямой. Допустим, что нам надо определить объем спроса для цены p, которая лежит между табличными значениями цены р1 и р2 которым соответствуют объемы спроса Q1 и Q2 Тогда искомый объем спроса Q для цены р приближенно равен
Если, например, объем спроса на картофель при цене 10 руб. равен 400 т, а при цене 15 руб. — 300 т (см. табл. 2.1), то объем спроса при цене 12 руб. приближенно равен (3/5) × 400 + (2/5) × 300 = 360 (т). Говоря о функциях спроса, часто используют понятия «спрос» и «изменение спроса». Здесь нередко возникает путаница, вызванная тем, что термин «спрос» используют для обозначения различных понятий: объема спроса, функции спроса и кривой спроса. Увеличение спроса в первом случае означает увеличение объема спроса, вызванное изменением цены товара, во втором случае — увеличение объема спроса для всех цен одновременно, в третьем случае — сдвиг кривой спроса вправо. Причины, вызывающие сдвиг кривой спроса, называют неценовыми факторами спроса. Приведем примеры неценовых факторов спроса: - увеличение доходов потребителей приводит к сдвигу кривой спроса на яблоки вправо (увеличение спроса); - снижение цены на маргарин приводит к сдвигу кривой спроса на масло влево (сокращение спроса); - успешная реклама автомобиля «ИЖ» приводит к сдвигу кривой спроса на него вправо (увеличение спроса); - резкое похолодание приводит к сдвигу кривой на мороженое влево (сокращение спроса); - ожидание общего повышения цен приводит к сдвигу кривой спроса на растительное масло вправо (увеличение спроса). Закон спроса выражает обратную зависимость между ценой и объемом спроса: при снижении цены объем спроса растет, и наоборот. Закон спроса нарушается для товаров Гиффена и товаров Веблена.
Товары Гиффена. Товар Гиффена (назван именем Роберта Гиффена — экономиста XIX в.) — очень редко встречающийся товар, для которого спрос растет с ростом цены и падает вместе с падением цены. Такое поведение спроса встречается в слаборазвитых странах, когда потребители настолько бедны, что тратят большую часть своего дохода на самые дешевые продукты, необходимые для существования. Есть страны, например, где большая часть населения питается в основном рисом. Если же цена на рис падает, то у людей появляется возможность истратить часть денег на более питательный продукт, скажем на мясо. Потребление риса при этом снижается. Товары Веблена (названы именем экономиста-социолога XIX в. Торстена Веблена). К этим товарам относятся предметы роскоши, такие как ювелирные изделия, модные духи, одежда, оригинальные произведения искусств. Если такие товары выпускаются в продажу по низкой цене, они теряют привлекательность для снобов, и, как следствие, спрос на них может сократиться. С увеличением цены, наоборот, спрос может возрасти. На рис. 3.3 показано, как может меняться рыночный спрос на товары, которые мы сейчас назвали.
Движение вдоль линии спроса и смещение линии спроса. Рассмотрим линию рыночного спроса на товар X, представленную на рис. 3.4. Предположим, что начальная цена единицы товара была 20 руб. и спрос был в объеме 500 единиц. На линии спроса это состояние отражает точка А. Если бы цена упала до 10 руб., то при тех же прочих условиях спрос возрос бы до 600 единиц, т. е. состояние рынка переместилось бы из точки А в точку В. Если бы цена увеличилась до 30 руб. за единицу, спрос упал бы до 400 единиц, и состоянию соответствовала бы точка С. Таким образом, линия рыночного спроса на товар X отражает эффект, который оказывает изменение цепы товара X на спрос при сохранении всех остальных условий неизменными. Предположим теперь, что изменился еще какой-то фактор, оказывающий влияние на спрос. Допустим, национальный доход вырос настолько, что каждый имеет возможность тратить больше денег на приобретение товаров. В этом случае спрос на товар X увеличится при любых ценах. Это значит, что мы должны будем нарисовать новую линию, отражающую связь между ценой и спросом. На рис. 3.5 показан пример того, как может переместиться линия спроса. Товары Гиффена встречаются среди дешевых товаров, которые представляют основной продукт питания бедняков. Если такой продукт (например, картофель) дорожает, то бедняки вынуждены сократить потребление других, более дорогих и качественных продуктов (мяса, сыра и др.). Поскольку наш товар остается сравнительно дешевым продуктом, объем спроса на него растет, что в некоторой степени компенсирует отказ от качественных продуктов. Товары Веблена встречаются среди дорогих товаров, которые приобретаются богатыми для демонстративного потребления: дорогие шубы, бриллианты. Цена в этом случае представляет собой основное потребительское качество товара, а потому чем она выше, тем больше объем спроса. На рис. 2.1 изображена кривая спроса. Ее сплошной участок отвечает «обычному» товару, для которого закон спроса выполняется. Пунктирные участки отвечают соответственно товару Веблена (верхний) и товару Гиффена (нижний).
Рис. 2.1. Кривая спроса
На рис. 2.2 показано различие между увеличением объема спроса (показано стрелкой, направленной вдоль кривой спроса D1) и увеличением спроса (показано сдвигом кривой спроса из положения D1 в положение D2). В первом случае объем спроса увеличился в результате снижения цены. Во втором случае объем спроса увеличился для каждой цены в результате воздействия одного или нескольких неценовых факторов спроса.
Рис. 2.2 Увеличение объема спроса и сдвиг кривой спроса
Предложение Выберем рынок какого-нибудь конкретного товара и возьмем любого продавца на этом рынке. Зафиксируем теперь цену товара. Наш продавец за определенный промежуток времени желает и способен продать некоторое количество товара по данной цене. Это количество называют объемом (количеством) индивидуального предложения продавца при данной цене. Объем индивидуального предложения зависит от многих факторов: цены данного товара, величины затрат, которых требует от нашего производителя производство данного товара; затратности производства других товаров, на которые может «переключиться» наш производитель, и их цен, налогов и дотаций, прочих условий. Рассмотрим теперь всех продавцов в совокупности. Объем рыночного предложения есть количество товара, которое желают и способны продать все продавцы вместе в единицу времени при данной цене. Эта величина равна сумме объемов индивидуального предложения всех продавцов при данной цене. Обычно объем рыночного предложения называют для краткости просто объемом предложения. То есть в случае, когда не указано прилагательное «индивидуальный» или «рыночный», речь идет о рыночном показателе. Цена предложения — это минимальная цена, по которой продавцы согласны продать определенное количество данного товара. Зависимость объема предложения от цены товара называют функцией предложения, а ее график называют кривой (линией) предложения. функцию предложения обозначают через Qs(p) или S(p) (supply — англ., предложение). Функция предложения обычно задается аналитическим, табличным или графическим способом. Если функция предложения задается аналитическим способом, то объем предложения рассчитывается путем подстановки значения цены в некоторую формулу, например: Объем предложения = 20 × Цена – 100, или Qs = 20р – 100. При цене товара, равной семи единицам, объем предложения будет равен 40 единицам (20 × 7 – 100). При использовании аналитического способа необходимо учитывать, что если при подстановке в формулу некоторого значения цены получается отрицательное число, то объем предложения считают равным нулю. Так, в приведенном выше примере объем предложения при цене три единицы равен нулю, поскольку подстановка этой цены в формулу дает минус 40. Цена, начиная с которой объем предложения становится ненулевым, называется минимальной ценой предложения. В нашем примере минимальная цена предложения равна пяти единицам. Это значит, что даже при самом незначительном увеличении данной цены найдутся продавцы, желающие продать некоторое количество товара по новой цене. Если функция предложения задается табличным способом, значения цены записываются в первом столбце таблицы, а соответствующие объемы предложения — во втором ее столбце. Для приближенной оценки объема предложения при цене, не указанной в таблице, можно использовать формулу из предыдущего раздела. Если, например, объем предложения на картофель при цене 10 руб. равен 200 т, а при цене 15 руб. — 300 т, то объем предложения при цене 14 руб. приближенно равен (1/5) × 200 + (4/5) × 300 = 280 (т). Говоря о функциях предложения, часто используют понятия «предложение» и «изменение предложения». Здесь, как и в случае с понятием «спрос», нередко возникает путаница, вызванная тем, что термин «предложение» используют для обозначения различных понятий: объема предложения, функции предложения и кривой предложения. Увеличение предложения в первом случае означает увеличение объема предложения, вызванное изменением цены товара, во втором случае — увеличение объема спроса для всех цен одновременно, в третьем случае — сдвиг кривой предложения вправо. Причины, вызывающие сдвиг кривой предложения, называют неценовыми факторами предложения. Приведем примеры неценовых факторов предложения: - увеличение цены на масло приводит к сдвигу кривой предложения сыра влево, поскольку молокозаводы «переключаются» на производство более выгодного товара (масло) и сокращают производство сыра (сокращение предложения); - увеличение цены на молоко приводит к сдвигу кривой предложения сыра влево, поскольку увеличиваются издержки производства сыра, при этом число производителей сыра, затраты которых на единицу продукции меньше любой заданной цены, уменьшается (сокращение предложения); - широкое внедрение прогрессивной технологии производства сыра сокращает затраты на единицу продукции и сдвигает тем самым кривую предложения вправо (увеличение предложения); - введение акциза (фиксированного налога на единицу продукции, взимаемого с продавца) сдвигает кривую предложения влево (сокращение предложения). Закон предложения выражает прямую зависимость между ценой и объемом предложения: при увеличении цены объем предложения растет, и наоборот. Данный закон нарушается для кривых предложения труда, поскольку при достаточно больших ценах труда (ставках заработной платы) продавец труда (наемный работник) может позволить себе сократить время работы, чтобы в освободившееся время использовать свой высокий доход. Поэтому, начиная с некоторого значения ставки заработной платы, функция предложения труда может убывать. Рассмотрим подробнее сдвиг кривой предложения в результате введения акцизного налога. В этом случае функцию предложения удобнее записывать, выражая цену через объем производства: p = f(Qd) Тогда минимальная цена предложения будет равна P0 = f(0) — точка пересечения кривой предложения с осью ординат. Это число равно издержкам на единицу продукции у самого эффективного (низкозатратного) производителя. После введения акцизного налога его величина (T) будет включена в издержки всеми производителями, минимально возможные издержки увеличатся до р0 + Т, а кривая предложения сдвинется вверх на Г единиц. В результате новая функция предложения будет задаваться формулой p = f(Qd) + T Если, например, исходная функция предложения задается формулой p = 2Q + 10, то минимально возможные издержки на единицу продукции равны 10. После введения акциза в размере трех единиц новая функция предложения будет задаваться формулой p = 2Q + 13. На рис. 2.3 изображена кривая предложения. Стрелка вдоль этой кривой отображает сокращение объема предложения в результате уменьшения цены.
Рис. 2.3 Кривая предложения На рис. 2.4 показано сокращение предложения (сдвиг кривой предложения влево вверх) в результате введения акцизного налога.
Рыночное равновесие Рыночное равновесие есть ситуация, когда объем спроса равен объему предложения при некоторой цене товара. Эта цена называется равновесной ценой, а соответствующий ей объем спроса (и предложения) — равновесным объемом. Если цена больше равновесной цены, то предложение превышает спрос, и имеет место избыток предложения. Если цена меньше равновесной, то спрос превышает предложение, и имеет место дефицит предложения (избыток спроса).
Рис. 2.4. Сдвиг кривой предложения в результате введения акциза
Объем продаж при некоторой цене равен минимальному значению из соответствующих объемов спроса и предложения. Если функция спроса убывает, а функция предложения возрастает (а именно так обычно и бывает), то при равновесной цене объем продаж максимален. На рис. 2.5 рыночное предложение изображено точкой пересечения кривых спроса и предложения (точка Е). Равновесная цена обозначена через р0, равновесный объем продаж — через Q0. График зависимости объема продаж от цены выделен жирной линией. Если функции спроса и предложения заданы аналитическим способом, то равновесную цену и равновесный объем продаж вычисляют, приравнивая эти функции друг к другу. Если, например, функция спроса D = 7 – 2р, а функция предложения S = 4р – 5, то равновесная цена находится как решение уравнения 7 – 2р = 4р – 5, отсюда равновесная цена равна двум единицам. Подставляя равновесную цену в функцию спроса (или предложения), получим равновесный объем продаж, равный трем единицам. Если после подстановки получается отрицательное значение объема, это значит, что кривые спроса и предложения не пересекаются, и равновесие на рынке не достигается.
Рис. 2.5 Рыночное равновесие
Если функции спроса и предложения заданы табличным способом, равновесную цену и равновесный объем легко определить, когда при некоторой цене, указанной в обеих таблицах, объем спроса совпадает с объемом предложения. Данная цена и является равновесной ценой. Если это условие не выполняется, то необходимо использовать приближенные методы расчета, рассмотренные в предыдущих главах. В табл. 2.2 представлен простой случай определения равновесной цены. Поскольку объемы спроса и предложения совпадают при цене 14, она и является равновесной. Таблица 2.2 Простой случай определения равновесной цены
В табл. 2.3 представлен более сложный случай определения равновесной цены, поскольку в таблице не имеется пары равных значений спроса и предложения. Таблица 2.3 Сложный случай определения равновесной цены
Из таблицы следует, что равновесная цена больше 14, обозначим ее через р. Используя формулу (2.1), получим приближенное значение равновесного спроса: (р – 14) / 4 × 20 + (18 – р) / 4 × 40. Используя ту же формулу, получим приближенное значение равновесного объема предложения: (р – 14) / 2 × 48 + (16 – р) / 2 × 36. Приравнивая полученные два выражения, получим приближенное значение равновесной цены, равное 14,36. Равновесный объем продаж равен приблизительно 38,2. Рассмотрим вопрос об изменении рыночного равновесия. При статическом подходе к этой проблеме рассматривают два состояния равновесия: до и после изменения. При динамическом подходе рассматривают ряд последовательных моментов времени, что позволяет детально исследовать сам процесс изменения равновесия. Примером статического анализа изменения рыночного равновесия является введение дотации на некоторый товар — фиксированной суммы, которая безвозмездно выплачивается государством производителю на каждую произведенную единицу продукции (учебники, медицинские услуги и т. п.). Дотация является, по сути дела, «отрицательным акцизным налогом», что позволяет нам использовать результаты предыдущего раздела, относящиеся к сдвигу кривой предложения. В частности, дотация в размере R сокращает удельные издержки производителей на эту величину и сдвигает кривую предложения на R единиц вниз. При этом равновесная цена уменьшается с р1 дор2, а равновесный объем продаж увеличивается с Q1 до Q2 (рис. 2.6).
Рис. 2.6 Изменение рыночного равновесия после введения дотации На рис. 2.6 видно, каким образом распределяются выгоды от дотации R между покупателями и продавцами на рынке. Хотя дотация выплачивается продавцу, покупатель получает выгоду от нее в виде снижения равновесной цены товара на величину Rd = p1 – p2. Оставшаяся часть дотации, равная Rs = R – Rd, достается продавцу. Аналогично распределяется акцизный налог. Соотношение между частями, на которые делится дотация, зависит от углов наклона кривых спроса и предложения к оси цен. Если кривая спроса круче, чем кривая предложения, то продавец получает большую часть дотации (или платит большую долю акциза). Если же кривая предложения круче, чем кривая спроса, то покупатель получает большую долю дотации (или платит большую долю акциза). Случается, что объем спроса не зависит от цены товара (инсулин, спиртные напитки в целом и др.). Тогда кривая спроса параллельна оси цен, и покупатели получают всю дотацию целиком или платят весь акцизный налог.
Паутинообразная модель Примером динамического анализа изменения рыночного равновесия является так называемая паутинообразная модель. Будем считать, что изменения на рынке происходят каждый день. Обозначим через i порядковый номер дня, а через Di, Si и pi — объем спроса, объем предложения и цену в i-й день соответственно. Предположим, что если объемы спроса и предложения не совпадают, то цена будет изменяться до тех пор, пока новый объем спроса не сравняется со старым объемом предложения: Di+1 = Si В результате нескольких описанных изменений рыночная цена может как приближаться к своему равновесному значению, так и удаляться от него. Рассмотрим два примера. Пример 1 Функция спроса D = 40 – 10р, функция предложения S = 5р – 5. Начальная цена равна 2. Найдем объемы спроса и предложения, а также цену в первые три дня. Первый день. Цена равна 2. Объем спроса равен 20, объем предложения равен 5. Имеет место дефицит предложения, поэтому цена будет расти до тех пор, пока спрос не сократится до 5: 40 – 10p = 5, отсюда p = 3,5. Второй день. Цена равна 3,5. Объем спроса равен 5, объем предложения равен 12,5. Имеет место избыток предложения, поэтому цена будет падать до тех пор, пока спрос не увеличится до 12,5: 40 – 10p = 12,5, отсюда p = 2,75. Мы видим, что рыночная цена приближается к своему равновесному значению, равному 3 (оно рассчитывается из условия равенства функций спроса и предложения), причем объемы спроса и предложения постепенно сближаются по величине. Запишем полученные результаты в таблицу (табл. 2.4). Таблица 2.4. Паутинообразная модель: стремление к равновесию
Пример 2 Функция спроса D = 30 – 2р, функция предложения S = 3p – 10. Начальная цена равна 6. Найдем объемы спроса и предложения, а также цену за первые три дня. Первый день. Цена равна 6. Объем спроса равен 18, объем предложения равен 8. Имеет место дефицит предложения, поэтому цена будет расти до тех пор, пока спрос не сократится до 8, отсюда новая цена равна 11 и т. д. Действуя так же, как и в первом примере, получим необходимые результаты и запишем их в таблицу (табл. 2.5). Таблица 2.5 Паутинообразная модель: «уход» от равновесия
Мы видим, что цена все больше удаляется от своего равновесного значения, равного 8, причем модуль разности объемов спроса и предложения постепенно увеличивается. Доказано, что если функции спроса и предложения являются линейными, т. е.: D = а – bp; S = с + dp, то характер изменения цены зависит от соотношения параметров b и d: - если b > d,m цена стремится к равновесному значению (пример 1); - если b < d, то цена «убегает» от равновесного значения (пример 2); - если b = d, то цена последовательно принимает два различных значения, среди которых нет равновесного. На рис. 2.7 представлены два случая паутинообразного изменения цены. В первом случае (рис. 2.7, а) угол к оси объемов у кривой спроса меньше по сравнению с кривой предложения, и цена стремится к своему равновесному значению. Во втором случае (рис. 2.7, б), наоборот, кривая спроса расположена круче по отношению к оси объемов, чем кривая предложения, и колебания цены вокруг равновесного значения увеличиваются.
Ценовая эластичность спроса Эластичность (E) есть показатель, характеризующий чувствительность значения функции к изменению ее аргумента. В отличие от производной функции эластичность не имеет размерности (а это чрезвычайно важно при сравнении характеристик функций спроса на различных рынках) и определяется как результат деления относительного изменения значения функции на относительное изменение аргумента:
Рис. 2.7 Паутинообразная модель
Преобразовав эту формулу и предположив, что абсолютное изменение аргумента функции невелико, получим другое представление эластичности:
Таким образом, эластичность равна производной функции, умноженной на отношение аргумента и значения функции. Поэтому знак коэффициента эластичности определяется знаком производной, однако эластичность весьма сложным образом связана с углом наклона графика функции к оси абсцисс и поэтому не имеет простой геометрической интерпретации. Ценовая эластичность спроса (Ed) есть результат деления относительного изменения объема спроса на относительное изменение цены, умноженный на минус единицу:
где D — спрос, р — цена. При определении ценовой эластичности спроса перед формулой эластичности поставлен знак «минус». Это связано с тем, что обычно знаки изменений спроса и предложения противоположны и отношение приростов отрицательно. Знак «минус» в определении делает коэффициент эластичности в большинстве случаев положительным, что удобно в применении. Например, если при увеличении цены на 2% величина спроса уменьшилась на 3%, то ценовая эластичность спроса равна 3/2 = 1,5. Ценовая эластичность спроса показывает, на сколько процентов изменится объем спроса при изменении цены товара на один процент. Она характеризует замещаемостъ данного товара другими товарами в потреблении. Спрос эластичен, если ценовая эластичность спроса больше единицы. В этом случае при незначительном повышении цены объем спроса существенно уменьшается. Спрос эластичен на товары, которые легко замещаются в потреблении другими товарами. Например, маргарин одной марки замещается маргарином другой марки, апельсины замещаются мандаринами и т. д. Спрос неэластичен, если ценовая эластичность спроса лежит в пределах от нуля до единицы. В этом случае относительное изменение цены превышает относительное изменение спроса, т. е. спрос слабо чувствителен к изменению цены. Спрос неэластичен на товары, которые слабо замещаются в потреблении другими товарами. Например, соль и пшеничная мука фактически не имеют заменителей. Спрос абсолютно эластичен, если ценовая эластичность спроса является бесконечно большой величиной. Это случается, когда имеется единственная цена, по которой товар покупается в неограниченном количестве, при этом любой другой цене отвечает нулевой спрос. Примером служит закупка правительством страны зерна у своих фермеров по фиксированной цене с целью поддержать отечественных сельскохозяйственных производителей. Спрос абсолютно неэластичен, если ценовая эластичность спроса равна нулю. В этом случае изменение цены не влияет на объем спроса. Примерами служат товары, без которых привычная жизнедеятельность человека нарушается: инсулин для больных сахарным диабетом, кофе и т. д. Единичная эластичность спроса имеет место, когда ценовая эластичность спроса равна единице. Этот случай интересен тем, что изменение цены не влияет на суммарную выручку продавцов на рынке. Например, при цене 3 руб. купят 12 т яблок, при цене 4 руб. — 9 т и т. д. В любом случае выручка составит 36 тыс. руб. Аналитический способ вычисления ценовой эластичности спроса применяют в случае, когда функция спроса задана формулой. При этом используют формулу, выражающую эластичность через производную функции. Рассмотрим частный случай линейной функции спроса: D = 12 – 3р. Учитывая, что производная данной функции спроса по цене равна - 3, получим формулу зависимости ценовой эластичности спроса от цены:
На рис. 2.8 отмечены все возможные случаи эластичности для линейной функции спроса.
Рис. 2.8 Ценовая эластичность спроса для линейной функции спроса Если цена равна нулю, то ценовая эластичность спроса также равна нулю, т. е. спрос абсолютно неэластичен (точка А). Если цена равна максимальной цене спроса, равной 4, то ценовая эластичность спроса бесконечно велика, т. е. спрос абсолютно эластичен (точка В). Если цена равна 2 (половине максимальной цены спроса), то ценовая эластичность спроса равна единице (точка С). Если цена больше 2, но меньше 4, то спрос эластичен (отрезок ВС). Если цена больше 0, но меньше 2, то спрос эластичен (отрезок АС). Табличный способ вычисления ценовой эластичности спроса представлен в табл. 2.6. В третьем столбце таблицы рассчитаны относительные изменения цены при ее увеличении от 10 до 12 и от 12 до 14. В четвертом столбце указаны соответствующие относительные изменения объема спроса. В пятом столбце определены значения ценовой эластичности спроса посредством деления соответствующих чисел в четвертом и третьем столбцах. Таблица 2.6 Расчет ценовой эластичности спроса
Графический способ вычисления ценовой эластичности спроса представлен на рис. 2.9.
Рис. 2.9. Графический способ вычисления ценовой эластичности спроса
Предположим, что необходимо найти ценовую эластичность спроса в точке С. Для этого через эту точку проведем касательную к кривой спроса и получим точки ее пересечения с осями координат: А и В. Доказано, что ценовая эластичность спроса равна отношению длин отрезков, на которые точка С делит отрезок АВ, а именно:
Данный способ удобно использовать при анализе ценовой эластичности спроса линейной функции, поскольку для нее кривая спроса совпадает с касательной (рис. 2.8). В частности, из приведенной выше формулы сразу следует, что ценовая эластичность спроса для точки, делящей график линейной функции пополам, равна единице. Аналитический и графический способы позволяют достаточно точно определить значение ценовой эластичности спроса для конкретной цены или, как говорят, в конкретной точке. Поэтому в этих случаях ценовую эластичность спроса называют точечной. Однако при вычислении ценовой эластичности спроса табличным способом возникает проблема, связанная с тем, что в зависимости от того, какую из двух цен считают исходной, получают два разных значения эластичности. Причем с увеличением разности между двумя ближайшими «табличными» ценами результат становится все более неопределенным. Поэтому вводят понятие дуговой эластичности спроса. Дуговая эластичность спроса есть характеристика ценовой эластичности спроса, относящаяся не к конкретной цене, а к некоторому промежутку ее изменения. Этот показатель не зависит от того, какую цену считают исходной, а какую — конечной. Если при изменении цены от р1 до р2 спрос изменился от Q1 до Q2, то дуговая эластичность спроса находится по формуле:
Пример 3 Рассчитаем дуговую эластичность спроса, если при увеличении цены с 10 до 12 руб. спрос сократится с 60 до 40 т (см. табл. 2.6):
Анализируя ценовую эластичность спроса, необходимо отметить, что этот показатель зависит от фактора времени. В длительном периоде спрос более эластичен, чем в коротком, поскольку для приспособления к новой цене необходимо время. С течением времени могут появиться относительно дешевые товары-заменители либо потребители постепенно отвыкнут от потребления подорожавшего товара.
|



 (2.1)
(2.1)