 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Эвристические алгоритмы распределения
Ресурсов на сетевом графике произвольного вида
2.4.1. Задача минимизации расхода ресурсов при заданном директивном сроке выполнения проекта Допустим, что каждая работа комплекса выполнима во временном интервале Алгоритм: 1. Примем 2. Для работ 3. На основании полученной динамической последовательности определить продолжительности операций 4. Положить
2.4.2. Задача минимизации времени выполнения проекта при заданном количестве ресурсов Комплекс работ задан следующим сетевым графиком (рис.2.6).
Рис. 2.6. Не принимая в расчет потребление ресурсов, получим критическое время проекта Таблица 2.7
Отыскание точного решения подобного рода задач достаточно сложно, несмотря на неявное предположение о взаимозаменяемости ресурсов.
Эвристические алгоритмы составления рационального расписания при распределении ограниченных ресурсов Для минимизации времени реализации проекта при ограничении на нескладируемые ресурсы используют правила предпочтения при выборе работы для включения в расписание: 1-ое правило. При назначении планового срока выполнения работы предпочтение отдается той операции, у которой минимален поздний срок свершения 2-ое правило. При включении в расписание предпочтение отдается той работе, которая предполагает большее потребление ресурсов, т.е. с Применение 2-ого правила предпочтения к примеру, заданному рис. 2.6, приводит к следующему расписанию (табл. 2.8).
Таблица 2.8
Вычислительную эффективность оценивают по нижней границе решения - максимуму из: · времени исполнения проекта наличными «мощностями» без учета топологии сети
· критической продолжительности проекта Относительная погрешность результата составит величину
Литература 1. Конюховский П.В. Математические методы исследования операций в экономике. – СПб.: Изд-во СПбГУ, 2008. 2. Таха Х. Введение в исследование операций. - М.: Мир,1985. 3. ГлуховВ.В., Медников М.Д., Коробко С.В. Математические методы для менеджеров. – СПб.: «Лань», 2005. 4. Мардас А.Н., Королев А.В. Математические методы в управлении и экономике. Учебное пособие. – СПб.: СПбГЭТУ «ЛЭТИ», 2007. |



 . Возможно условие
. Возможно условие  . Тогда для каждой из работ необходимо определить величину
. Тогда для каждой из работ необходимо определить величину  из допустимого промежутка
из допустимого промежутка  и найдем первый возможный критический путь
и найдем первый возможный критический путь  с продолжительностью
с продолжительностью 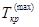 . Если
. Если  , то распределение ресурсов, обеспечивающее
, то распределение ресурсов, обеспечивающее  , приводит к оптимальному решению, причем
, приводит к оптимальному решению, причем  . Если же нет, то осуществляем переход ко второму шагу алгоритма.
. Если же нет, то осуществляем переход ко второму шагу алгоритма.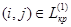 произвести оптимальное распределение ресурсов как для последовательного сетевого графика, ориентируясь на условие
произвести оптимальное распределение ресурсов как для последовательного сетевого графика, ориентируясь на условие  для
для  и исключить из множества критических работ операции с
и исключить из множества критических работ операции с  .
. и
и 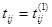 для
для  и
и  . Проверить условие
. Проверить условие  . Если оно выполняется, то план распределения ресурсов, полученный на данном шаге, оптимален. В противном случае перейти к п.2.
. Если оно выполняется, то план распределения ресурсов, полученный на данном шаге, оптимален. В противном случае перейти к п.2.
 . Построив далее таблицу 2.7 для отражения количества исполнителей, задействованных в определенный день, установим, что выполнение проекта за 9 дней возможно, если мы располагаем 7 исполнителями.
. Построив далее таблицу 2.7 для отражения количества исполнителей, задействованных в определенный день, установим, что выполнение проекта за 9 дней возможно, если мы располагаем 7 исполнителями.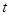


 завершающего события
завершающего события 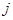 максимален ранний срок
максимален ранний срок  свершения начального события i.
свершения начального события i. , где
, где  означает общие затраты (затраты в единицу времени).
означает общие затраты (затраты в единицу времени). ;
; при отсутствии ограничений на ресурсы.
при отсутствии ограничений на ресурсы. ,
,