 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Метод ветвей и границ в применении к теории расписаний
Дисциплина «Математические методы исследования операций»
Иллюстрационный (раздаточный) материал к теме «Теория расписаний»
Лекции 11 - 12. Учебные вопросы: 1. Задачи календарного планирования 2. Алгоритм Джонсона 3. Метод ветвей и границ в применении к теории расписаний 4. Задача коммивояжера и алгоритм ее решения методом ветвей и границ 5. Оптимизация расписаний
1. Задачи календарного планирования Задачи календарного планирования представляют собой задачи упорядочения во времени множества работ, выполняемых на заданном оборудовании. Календарный план является моделью производства, отражает основные его особенности. Чем совершеннее эта модель, тем эффективнее планирование производства. Поэтому разработка оптимальных календарных планов является одной из важнейших задач теории расписаний. Теория расписаний оперирует следующими основными понятиями: · операция — элементарная работа, подлежащая выполнению; · машина—устройство для выполнения отдельных операций. Каждая операция характеризуется: · индексом · индексом · временем Множество всех машин, предназначенных для выполнения операций, принято называть системой обслуживания. Задача составления расписания заключается в определении оптимальной последовательности выполнения операций каждой машиной. При этом обобщенное понятие «машина» может иметь самый различный физический смысл. Например, станок для обработки деталей, бригада рабочих для выполнения ремонтных работ, аудитория для проведения занятий, автомобиль для перевозки грузов и т. д. В зависимости от порядка обработки изделий машинами различают конвейерную систему обслуживания и систему с произвольным порядком обработки изделий. В конвейерной системе порядок обработки для всех изделий одинаков, т. е. все изделия обслуживаются машинами в одной и той же последовательности. В системе с произвольным обслуживанием последовательность обработки изделий машинами различна. Методы решения задач теории расписаний можно разделить на две группы: точные и приближенные. Из точных методов наиболее широко используется метод ветвей и границ. Для решения задач большой размерности используются приближенные методы, в основу которых положены различные эвристические правила определения порядка обработки изделий. Основной недостаток приближенных методов — невозможность оценить точность решения. При определении оптимальной последовательности обработки изделий в зависимости от характера задач теории расписаний используются следующие основные критерии: 1. Минимум общей продолжительности обработки изделий. 2. Минимум максимального отставания сроков обработки изделий от заданных. 3. Минимум времени простоя машин или межоперационных задержек изделий. Задачей теории расписаний, имеющей большое прикладное значение в инновационном менеджменте, является так называемая общая задача теории расписаний, формулируемая следующим образом. Имеется т машин для обработки п изделий. Каждое из изделий должно пройти обработку на всех машинах в определенном порядке. Этот порядок может быть одинаковым или различным для всех изделий. При этом каждая машина может выполнять только один тип операций, одновременно на одной машине может обрабатываться не более одного изделия, начатая обработка изделия на машине не может быть прервана, последующая операция по обработке каждого изделия может начаться только после выполнения предыдущей. Для заданной матрицы Решение общей задачи теории расписаний перебором всех возможных вариантов практически невозможно из-за большого количества вариантов. Если порядок обработки для всех изделий одинаков, число вариантов определяется величиной Алгоритм Джонсона Наиболее простой и эффективный вычислительный алгоритм разработан для решения задачи теории расписаний, когда необходимо обработать п изделий на двух машинах Обозначим:
Требуется определить порядок обработки изделий, минимизирующий время обработки всех изделий. Алгоритм решения этой задачи состоит из следующих шагов. 1. Среди чисел ( 2. Если 3. Вычеркнуть изделие, введенное в календарный план, т. е. числа Поясним работу алгоритма на примере решения задачи, исходные данные для которой приведены в табл. 12.1. Минимальное значение Определив последовательность обработки, вычисляем общее время обработки всех изделий (табл. 12.2).
Таблица 12.1.
Таблица 12.2.
Момент окончания обработки i-того изделия на j-той машине определяется рекуррентным соотношением
Решение данной задачи прямым перебором потребовало бы 720 перестановок. Данный алгоритм может быть использован и при обработке изделий на трех машинах, если выполняется условие
где При выполнении одного из этих условий оптимальная последовательность обработки определяется по суммам Метод ветвей и границ в применении к теории расписаний Общим методом решения задач теории расписаний является метод ветвей и границ. При его применении ветвление дерева вариантов осуществляется следующим образом. На первом уровне исходное множество возможных последовательностей, содержащее п! вариантов, разбивают на п вариантов, на следующем уровне на (п-1) вариант и т. д. Выбор ветви для дальнейшего ветвления производят по рассчитанным значениям нижней границы решения для вершин, находящихся на данном уровне. Для примера рассмотрим случай трех машин, т.е. будем полагать Обозначим через U={1, 2, . . ., n} множество всех изделий. Допустим, что имеется множество изделий S={1, 2, . . ., k} (k<n), для которых составлено расписание и вычислено время их обработки на первой машине T1(S), на второй машине T2(S) и на третьей машине T3(S). Тогда нижняя граница для продолжительности обработки всех изделий может быть вычислена с помощью выражения
где
Основная трудность, однако, состоит в том, что определение такой оценки связано с большим объемом вычислений. Вместе с тем, при одинаковом порядке обработки задача трех станков, в принципе, может быть решена точно. В общем же случае последовательность обработки изделий на машинах может быть различной. Тогда каждая операция дополнительно характеризуется индексом k, который указывает порядковый номер операции при обработке Наиболее простой алгоритм решения задачи теории расписаний при различном порядке обработки изделий разработан для варианта, когда т=2, т.е. обработка изделий производится на двух машинах. В этом случае для решения используется модифицированный алгоритм Джонсона. Предварительно все множество изделий разбивается на четыре подмножества: [A]—подмножество изделий, которые обрабатываются только на первой машине; [B] — подмножество изделий, которые обрабатываются только на второй машине; {АВ} — подмножество изделий, для которых первая операция выполняется на первой машине, вторая — на второй; {ВА}— подмножество изделий, для которых первая операция выполняется на второй машине, вторая — на первой. С помощью алгоритма Джонсона определяется оптимальная последовательность обработки изделий, входящих в множество {АВ} и отдельно входящих в множество {ВА}. Минимальное время обработки всех изделий обеспечивается следующим порядком их обработки. На первой машине первоначально обрабатываются изделия из множества {АВ}, затем изделия из множества {А} и в последнюю очередь изделия из множества {ВА}. На второй машине последовательность обработки обратная. В первую очередь обрабатываются изделия из множества {ВА}, затем изделия из множества {В} и в последнюю очередь изделия из множества {АВ}. Последовательность обработки изделий из множества {АВ} и {ВА} соответственно определяется по обычному алгоритму Джонсона. Последовательность обработки изделий из множеств {А} и {В} может быть произвольной. Метод ветвей и границ, являющийся общим, практически может быть применен только для решения небольших задач. Чаще прибегают к использованию различных правил предпочтения, определяющих выбор очередной операции для включения ее в расписание: 1. Выбор операции с минимальной длительностью выполнения. 2. Выбор операции, относящейся к изделию с максимальной длительностью всех неупорядоченных операций. 3. Выбор операции, относящейся к изделию с минимальной длительностью выполнения всех неупорядоченных операций. 4. Равновероятный выбор очередной операции. Анализ результатов их применения показывает, что правило 2 дает наилучшие результаты, когда минимизируется общая длительность обработки всех изделий; правило 3 — когда минимизируется среднее время обработки одного изделия. Дальнейшее развитие метод правил предпочтения получил совместно с вероятностным подходом. В этом случае выбор операции для включения в расписание производится случайным образом с частотой, определяемой величиной функции предпочтения. Многократным повторением расчетов получают различные расписания, из которых выбирается наилучшее. Для планирования деятельности рабочих групп в инновационном менеджменте может быть использована минимаксная задача о назначениях. В терминах теории расписаний задача она формулируется следующим образом. Имеется п машин, на которых необходимо обработать п изделий. Каждая машина может обрабатывать только одно изделие. Задана квадратная матрица Таким образом, требуется минимизировать выражение
при ограничениях
Рассмотрим применение метода ветвей и границ к решению задачи (4.26)—(4.29). Введем обозначения:
Из теорем о седловой точке в задаче поиска условного экстремума следует, что если удается подобрать
и то оптимальному решению соответствует план, обеспечивающий
Таким образом, в задаче о назначениях рабочих групп для выполнения условия Алгоритм решения включает в себя следующие операции. В начале вычислительного процесса
Заменяем для элементов i,j где
Вычеркиваем
Проверяем условие
Рассмотрим применение метода ветвей и границ к решению задачи календарного планирования на конкретном примере, исходная матрица, для которого приведена в табл. 1. Определяем минимальные элементы каждой строки
Нужно заметить, что аналогичные операции по приведении матрицы выполняются и в венгерском методе. Приведенная матрица представлена в табл. 3, где около каждого нулевого элемента указана сумма минимальных элементов строки и столбца, в котором находится нулевой элемент при его замене на ∞. Максимальному значению
Вычеркивая первую строку и третий столбец, получаем матрицу приведенную в табл. 4. В первом столбце этой матрицы отсутствует нулевой элемент. Следовательно,
Так как выполняется условие Дальнейший процесс вычисления выполняется аналогичным образом и приведен в табл. 5.
Таблица 1
Таблица 2
Таблица 3
Таблица 4
Таблица 5
|



 принадлежности к определенному изделию;
принадлежности к определенному изделию; машины, на которой она выполняется;
машины, на которой она выполняется; выполнения операций по обработке
выполнения операций по обработке  -го изделия на
-го изделия на  -ой машине.
-ой машине.  .
. требуется определить такую последовательность обработки изделий, при которой общее время обработки всех изделий минимально.
требуется определить такую последовательность обработки изделий, при которой общее время обработки всех изделий минимально. , при различном порядке обработки
, при различном порядке обработки  . Очевидно, что перебрать все возможные варианты даже с использованием современных компьютеров весьма затруднительно.
. Очевидно, что перебрать все возможные варианты даже с использованием современных компьютеров весьма затруднительно. при одинаковом порядке обработки всех изделий (алгоритм Джонсона). Идея алгоритма основана на минимизации времени простоя второй машины.
при одинаковом порядке обработки всех изделий (алгоритм Джонсона). Идея алгоритма основана на минимизации времени простоя второй машины. - время обработки
- время обработки  - время обработки
- время обработки  ) найти наименьшее
) найти наименьшее 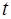 .
. , то поставить
, то поставить  -ое изделие на первое место рас-писания; если
-ое изделие на первое место рас-писания; если  , то поставить на последнее место. При наличии равных минимальных чисел
, то поставить на последнее место. При наличии равных минимальных чисел 
 -ое изделие ставится на первое место,
-ое изделие ставится на первое место,  -ое - на последнее. Если же одинаковы минимальные числа
-ое - на последнее. Если же одинаковы минимальные числа  ,то на первое место ставится изделие, которому соответствует меньшее время обработки на второй машине. При
,то на первое место ставится изделие, которому соответствует меньшее время обработки на второй машине. При  на последнее место ставится изделие, имеющее меньшее время обработки на первой машине.
на последнее место ставится изделие, имеющее меньшее время обработки на первой машине. и
и  , и повторить все перечисленные шаги алгоритма.
, и повторить все перечисленные шаги алгоритма.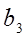 =1. Значит, третье изделие обрабатывается последним, т. е. шестым. Исключаем третье изделие из дальнейшего рассмотрения, определяем следующее минимальное значение
=1. Значит, третье изделие обрабатывается последним, т. е. шестым. Исключаем третье изделие из дальнейшего рассмотрения, определяем следующее минимальное значение  =3 и ставим пятое изделие на первое место в расписании. Аналогичным образом определяем порядок обработки всех оставшихся изделий.
=3 и ставим пятое изделие на первое место в расписании. Аналогичным образом определяем порядок обработки всех оставшихся изделий.
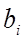

 - номер обработки изделия в расписании;
- номер обработки изделия в расписании; номер машины;
номер машины;
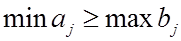 или
или  ,
,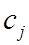 - время обработки
- время обработки  и
и  .
.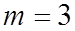 .
. , (4.22)
, (4.22) , (4.23)
, (4.23) , (4.24)
, (4.24) . (4.25)
. (4.25) -того изделия на
-того изделия на  -ой машине. Например, запись k=1, j=3, i=2 означает, что первая операция при обработке третьего изделия выполняется на второй машине.
-ой машине. Например, запись k=1, j=3, i=2 означает, что первая операция при обработке третьего изделия выполняется на второй машине. времени обработки
времени обработки  -го изделия
-го изделия  . Требуется распределить изделия по машинам таким об-разом, чтобы общее время обработки всех изделий было минимальным.
. Требуется распределить изделия по машинам таким об-разом, чтобы общее время обработки всех изделий было минимальным. , (4.26)
, (4.26) ; (4.27)
; (4.27) ; (4.28)
; (4.28) (4.29)
(4.29) - множество переменных
- множество переменных  ;
; - множество переменных
- множество переменных  - множество переменных
- множество переменных  - множество переменных
- множество переменных  - нижняя граница решения для ветви дерева возможных вариантов, составленной из элементов
- нижняя граница решения для ветви дерева возможных вариантов, составленной из элементов  ;
; - нижняя граница решения при условии, что
- нижняя граница решения при условии, что  , (вершина вводится в
, (вершина вводится в  - нижняя граница решения при условии, что
- нижняя граница решения при условии, что 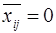 .
.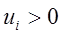 и
и  , такие, что
, такие, что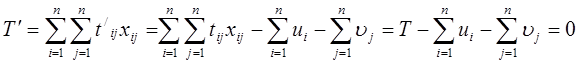
 ,
, или
или  .
. в каждой строке и в каждом столбце матрице
в каждой строке и в каждом столбце матрице  должен быть хотя бы один элемент
должен быть хотя бы один элемент  . Так как данное условие является необходимым, то величина
. Так как данное условие является необходимым, то величина  может быть принята в качестве нижней границы решения в методе ветвей и границ.
может быть принята в качестве нижней границы решения в методе ветвей и границ. ,
, 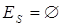 ,
,  . Определяем в каждой строке матрицы
. Определяем в каждой строке матрицы  и вычитаем его из элементов данной строки. Определяем в каждом столбце полученной матрицы минимальный элемент
и вычитаем его из элементов данной строки. Определяем в каждом столбце полученной матрицы минимальный элемент 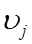 и вычитаем его из всех элементов данного столбца. Суммируя все элементы, которые вычитались из элементов строк и столбцов, определяем нижнюю границу решения задачи при выполнении каждой из работ за минимально возможное время:
и вычитаем его из всех элементов данного столбца. Суммируя все элементы, которые вычитались из элементов строк и столбцов, определяем нижнюю границу решения задачи при выполнении каждой из работ за минимально возможное время: .
. на
на  и снова определяем сумму минимальных элементов
и снова определяем сумму минимальных элементов  -ой строки и
-ой строки и  -го столбца. Выбираем для включения в множество
-го столбца. Выбираем для включения в множество  элемент
элемент 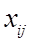 , для которого эта сумма
, для которого эта сумма  максимальна. Следовательно, при невключении в множество
максимальна. Следовательно, при невключении в множество  этого элемента матрицы времен нижняя граница решения возрастет и составит:
этого элемента матрицы времен нижняя граница решения возрастет и составит: .
. и каждого столбца
и каждого столбца  , вычисляем сумму этих элементов
, вычисляем сумму этих элементов  и нижнюю границу при включении в расписание данного элемента:
и нижнюю границу при включении в расписание данного элемента: .
. . Если условия выполняется, вводим в множество
. Если условия выполняется, вводим в множество  Æ. При его достижении принимаем
Æ. При его достижении принимаем  , выбираем ветвь с минимальным значением из тех значений нижней границы, для которых
, выбираем ветвь с минимальным значением из тех значений нижней границы, для которых  , и продолжаем процесс ветвления. Ветвление продолжается до тех пор, пока не будет найдено новое приближенное решение либо будет установлено, что по всем ветвям значение
, и продолжаем процесс ветвления. Ветвление продолжается до тех пор, пока не будет найдено новое приближенное решение либо будет установлено, что по всем ветвям значение  . Элементы матрицы
. Элементы матрицы  , приводящие к
, приводящие к  , и будут решением задачи.
, и будут решением задачи. и вычитаем их из элементов соответствующих строк. В результате получаем матрицу, приведенную в табл. 2. Определяем минимальные элементы в каждом столбце
и вычитаем их из элементов соответствующих строк. В результате получаем матрицу, приведенную в табл. 2. Определяем минимальные элементы в каждом столбце  и вычитаем их из элементов соответствующих столбцов. Нижняя граница
и вычитаем их из элементов соответствующих столбцов. Нижняя граница .
. соответствует
соответствует  . Выбираем любой из этих элементов, например
. Выбираем любой из этих элементов, например  . Тогда
. Тогда
 и
и .
. , то включаем в множество
, то включаем в множество  .
. j i
j i j i
j i
 j i
j i 3
3 1
1 j i
j i j i
j i 5
5 2
2 j i
j i j i
j i 4
4 3
3 j i
j i 2
2 5
5