 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Задача коммивояжера и алгоритм ее решения методом ветвей и границ
Задача теории расписаний при условии непрерывности процесса обработки изделий формулируется следующим образом. Имеется т машин и п изделий, обработка которых на всех машинах производится в одинаковой последовательности. При этом обработка каждого изделия должна осуществляться непрерывно, т. е. простои изделий между обработкой их на различных машинах не допускаются. Требуется определить такую последовательность обработки изделий, при которой общее время их обработки минимально. Рассмотренная задача сводится к известной задаче о коммивояжере. К этой же задаче сводится задача теории расписаний с одной машиной  при условии переналадки машины для обработки различных изделий. при условии переналадки машины для обработки различных изделий. Сформулируем задачу о коммивояжере в следующем виде. Имеется п+1 город, задана матрица  времени переезда из времени переезда из  -того города в -того города в  -тый. Выезжая из исходного города (будем ему приписывать индекс 0), коммивояжер должен побывать во всех остальных городах ровно по одному разу и вернуться в начальный город. Требуется определить порядок объезда городов, при котором суммарное время объезда минимально. -тый. Выезжая из исходного города (будем ему приписывать индекс 0), коммивояжер должен побывать во всех остальных городах ровно по одному разу и вернуться в начальный город. Требуется определить порядок объезда городов, при котором суммарное время объезда минимально. Задача коммивояжера называется симметричной при  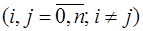 и несимметричной при и несимметричной при  . Возможен случай незамкнутой задачи коммивояжера, когда нет необходимости возвращаться в начальный город. Задача легко приводится к замкнутой путем введения . Возможен случай незамкнутой задачи коммивояжера, когда нет необходимости возвращаться в начальный город. Задача легко приводится к замкнутой путем введения  . Если начальный город не задан и объезд может начаться из любого города, задача может быть приведена к замкнутой введением фиктивного (нулевого) города, для которого . Если начальный город не задан и объезд может начаться из любого города, задача может быть приведена к замкнутой введением фиктивного (нулевого) города, для которого  и и  . В общем случае математически задача формулируется следующим образом. Требуется определить . В общем случае математически задача формулируется следующим образом. Требуется определить  . (12) . (12)
при ограничениях  (13) (13)
 (14) (14)
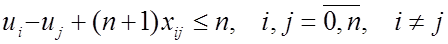 , (15) , (15)
где  — вещественные числа. — вещественные числа. Условия (13), (14) означают, что коммивояжер выезжает и въезжает в каждый город только один раз. Условие (15) предотвращает появление дополнительных замкнутых циклов. Действительно, положим  , если город , если город 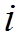 посещается на посещается на  шаге объезда шаге объезда  . Тогда на очередном шаге при . Тогда на очередном шаге при  будем иметь будем иметь  , ,
а при  (посещении города (посещении города  ) ) 
Задача (12)-(15) аналогична задаче о назначениях, за исключением условия (15). Кроме того, нельзя непосредственно возвращаться из города  в тот же город, что можно исключить, введя в тот же город, что можно исключить, введя  ∞. ∞. Рассмотрим сведение задачи теории расписаний при условии непрерывной обработки изделий к задаче о коммивояжере. Так как машины обрабатывают изделия независимо друг от друга, то одновременно в обработке может находиться несколько изделий. Возможность параллельной обработки изделий зависит от того, в какой последовательности производится обработка. Определим время  , в течение которого продолжается обработка , в течение которого продолжается обработка  -того изделия после завершения обработки -того изделия после завершения обработки  -того изделия. Очевидно, что -того изделия. Очевидно, что  , ,
где  — время обработки — время обработки  -того изделия на всех машинах; -того изделия на всех машинах;  — время, в течение которого — время, в течение которого  -тое и -тое и  -тое изделия одновременно находятся в обработке. -тое изделия одновременно находятся в обработке.
Значения  и и  можно найти с помощью выражений можно найти с помощью выражений  (16) (16)
 (17) (17)
где  - время обработки - время обработки  -того изделия на -того изделия на  -той машине; -той машине;
 - время от момента начала обработки - время от момента начала обработки  -того изделия до момента начала его обработки на -того изделия до момента начала его обработки на  -той машине -той машине  ; ;
 - время от момента завершения обработки - время от момента завершения обработки  -того изделия на -того изделия на  -той машине до момента окончания его обработки на последней -той машине до момента окончания его обработки на последней 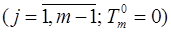 . .
Для сведения рассматриваемой задачи к задаче о коммивояжере введем фиктивное (нулевое) изделие, время обработки которого на любой машине равно нулю. Тогда получим  , так как совмещение времени обработки любого изделия с фиктивным невозможно, и , так как совмещение времени обработки любого изделия с фиктивным невозможно, и  , так как обработка фиктивного изделия , так как обработка фиктивного изделия  . Таким образом, данная задача сводится к задаче (12)— (15). . Таким образом, данная задача сводится к задаче (12)— (15).
Рассмотрим численный пример, исходные данные для которого приведены в табл. 12.20. Вычислив значения  и и  (табл. 12.21), с помощью выражения (17) определяем значения (табл. 12.21), с помощью выражения (17) определяем значения  (табл. 12.22). Введя фиктивное изделие, рассчитываем (табл. 12.22). Введя фиктивное изделие, рассчитываем  . . Таблица 12.20 | | | | |  k k | | | | | | | | | | | | | | | | | | | | | Таблица 12.21 Таблица 12.22  k i k i | | | | | | - | | | | | | - | | | | | | - | | | | | | - | Таблица 12.23  k i k i | | | | | |  | | ∞ | | | | | | | | ∞ | | | | | | | | ∞ | | | | | | | | ∞ | | | | | | | | ∞ | | Таблица 12.24  k i k i | | | | | | | ∞ | | | | | | | ∞ | | | | | | | ∞ | | | | | | | ∞ | | | | | | | ∞ |  | | | | | | Таблица 12.25  k i k i | | | | | |  0 0 | ∞ | 01 |  012 012 | 02 | 05 | | 08 | ∞ | | | | | 01 | | ∞ | | | | 02 | | | ∞ | | | 07 | | | | ∞ | Таблица 12.26  k i k i | | | | | | | ∞ | | | | ∞ | | | | | | | ∞ | | | | | | ∞ | Алгоритм решения задачи (10.12)— (10.15), по существу, совпадает с алгоритмом решения задачи о назначениях. Рассмотрим особенности этого алгоритма на примере, матрица  для которого представлена в табл. 12.23. После определения констант приведения (табл. 12.23 и 12.24) и вычитания их из соответствующих строк и столбцов получим матрицу (табл. 12.25), в каждой строке и в каждом столбце которой имеется нулевой элемент. Около каждого нулевого элемента указана величина для которого представлена в табл. 12.23. После определения констант приведения (табл. 12.23 и 12.24) и вычитания их из соответствующих строк и столбцов получим матрицу (табл. 12.25), в каждой строке и в каждом столбце которой имеется нулевой элемент. Около каждого нулевого элемента указана величина  . Максимальному значению . Максимальному значению  соответствует соответствует  . Так как первоначальное значение нижней границы . Так как первоначальное значение нижней границы  , ,
то  . .
Вычеркивая нулевую строку и второй столбец, получаем матрицу  , представленную в табл. 12.26, и определяем , представленную в табл. 12.26, и определяем  и и 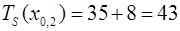 . . Вычитая константы приведения  из элементов соответствующих столбцов, получаем новую матрицу из элементов соответствующих столбцов, получаем новую матрицу  (табл. 12.27). Так как (табл. 12.27). Так как  вводим в множество вводим в множество   . В табл. 12.27 для исключения запрещенного полуцикла (0, 2; 2, 0) вместо . В табл. 12.27 для исключения запрещенного полуцикла (0, 2; 2, 0) вместо  подставляем подставляем  ∞. Аналогичная операция выполняется в табл. 12.28 ( ∞. Аналогичная операция выполняется в табл. 12.28 (  ∞) и 12.30 ( ∞) и 12.30 (  ∞). В остальном вычислительная процедура полностью аналогична вычислительной процедуре решения задачи о назначениях. ∞). В остальном вычислительная процедура полностью аналогична вычислительной процедуре решения задачи о назначениях. Таблица 12.27  k i k i | | | | | | 03 | ∞ |  6 6 | |  2 2 | ∞ | 01 | 05 | 03 | | 01 | | ∞ | | | 05 | | | ∞ | Таким образом, основная особенность решения задачи о коммивояжере по сравнению с решением задачи о назначениях заключается в предотвращении запрещенных циклов путем искусственного запрещения отдельных элементов матрицы за счет введения соответствующих значений  ∞. ∞. Таблица 12.28 Таблица 12.29  k i k i | | | | | | ∞ | | | ∞ | | | | 0 | | ∞ |  Таблица 12.30 Таблица 12.30
| k i | | | | ∞ |  ∞ ∞ | | 0∞ | 0∞ | В результате решения данного примера (табл. 12.25—12.30) находим приближенное решение  , которому соответствуют , которому соответствуют  . Анализ дерева возможных вариантов (рис. 12.3) показывает, что для всех ветвей дерева выполняется условие . Анализ дерева возможных вариантов (рис. 12.3) показывает, что для всех ветвей дерева выполняется условие  . Значит, полученное решение является оптимальным, и изделия нужно обрабатывать в последовательности 2, 3, 1, 4. Общее время обработки при этом будет Т=47. На рис. 12.4 изображены графики обработки изделий в оптимальной последовательности и в последовательности 1, 2, 3, 4. Неоптимизированному варианту соответствует общее время обработки Т=57. Таким образом, последовательность существенно влияет на время обработки всех изделий. . Значит, полученное решение является оптимальным, и изделия нужно обрабатывать в последовательности 2, 3, 1, 4. Общее время обработки при этом будет Т=47. На рис. 12.4 изображены графики обработки изделий в оптимальной последовательности и в последовательности 1, 2, 3, 4. Неоптимизированному варианту соответствует общее время обработки Т=57. Таким образом, последовательность существенно влияет на время обработки всех изделий.  
Оптимизация расписаний 
 
|




 при условии переналадки машины для обработки различных изделий.
при условии переналадки машины для обработки различных изделий. времени переезда из
времени переезда из  -того города в
-того города в  -тый. Выезжая из исходного города (будем ему приписывать индекс 0), коммивояжер должен побывать во всех остальных городах ровно по одному разу и вернуться в начальный город. Требуется определить порядок объезда городов, при котором суммарное время объезда минимально.
-тый. Выезжая из исходного города (будем ему приписывать индекс 0), коммивояжер должен побывать во всех остальных городах ровно по одному разу и вернуться в начальный город. Требуется определить порядок объезда городов, при котором суммарное время объезда минимально.
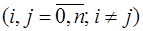 и несимметричной при
и несимметричной при  . Возможен случай незамкнутой задачи коммивояжера, когда нет необходимости возвращаться в начальный город. Задача легко приводится к замкнутой путем введения
. Возможен случай незамкнутой задачи коммивояжера, когда нет необходимости возвращаться в начальный город. Задача легко приводится к замкнутой путем введения  . Если начальный город не задан и объезд может начаться из любого города, задача может быть приведена к замкнутой введением фиктивного (нулевого) города, для которого
. Если начальный город не задан и объезд может начаться из любого города, задача может быть приведена к замкнутой введением фиктивного (нулевого) города, для которого  и
и  . В общем случае математически задача формулируется следующим образом. Требуется определить
. В общем случае математически задача формулируется следующим образом. Требуется определить . (12)
. (12) (13)
(13) (14)
(14)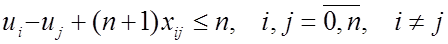 , (15)
, (15) — вещественные числа.
— вещественные числа. , если город
, если город 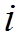 посещается на
посещается на  шаге объезда
шаге объезда  . Тогда на очередном шаге при
. Тогда на очередном шаге при  будем иметь
будем иметь ,
, (посещении города
(посещении города 
 в тот же город, что можно исключить, введя
в тот же город, что можно исключить, введя  ∞.
∞. , в течение которого продолжается обработка
, в течение которого продолжается обработка  -того изделия после завершения обработки
-того изделия после завершения обработки  -того изделия. Очевидно, что
-того изделия. Очевидно, что ,
, — время обработки
— время обработки  -того изделия на всех машинах;
-того изделия на всех машинах; — время, в течение которого
— время, в течение которого  и
и  можно найти с помощью выражений
можно найти с помощью выражений (16)
(16) (17)
(17) - время обработки
- время обработки  -той машине;
-той машине; - время от момента начала обработки
- время от момента начала обработки  ;
; - время от момента завершения обработки
- время от момента завершения обработки 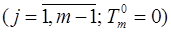 .
. , так как совмещение времени обработки любого изделия с фиктивным невозможно, и
, так как совмещение времени обработки любого изделия с фиктивным невозможно, и  , так как обработка фиктивного изделия
, так как обработка фиктивного изделия  . Таким образом, данная задача сводится к задаче (12)— (15).
. Таким образом, данная задача сводится к задаче (12)— (15). и
и  (табл. 12.21), с помощью выражения (17) определяем значения
(табл. 12.21), с помощью выражения (17) определяем значения  (табл. 12.22). Введя фиктивное изделие, рассчитываем
(табл. 12.22). Введя фиктивное изделие, рассчитываем  .
. k
k j i
j i







 k i
k i k i
k i
 k i
k i
 k i
k i 0
0 012
012 k i
k i для которого представлена в табл. 12.23. После определения констант приведения (табл. 12.23 и 12.24) и вычитания их из соответствующих строк и столбцов получим матрицу (табл. 12.25), в каждой строке и в каждом столбце которой имеется нулевой элемент. Около каждого нулевого элемента указана величина
для которого представлена в табл. 12.23. После определения констант приведения (табл. 12.23 и 12.24) и вычитания их из соответствующих строк и столбцов получим матрицу (табл. 12.25), в каждой строке и в каждом столбце которой имеется нулевой элемент. Около каждого нулевого элемента указана величина  . Максимальному значению
. Максимальному значению  соответствует
соответствует  . Так как первоначальное значение нижней границы
. Так как первоначальное значение нижней границы ,
, .
. , представленную в табл. 12.26, и определяем
, представленную в табл. 12.26, и определяем  и
и 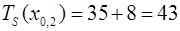 .
. из элементов соответствующих столбцов, получаем новую матрицу
из элементов соответствующих столбцов, получаем новую матрицу  вводим в множество
вводим в множество 
 . В табл. 12.27 для исключения запрещенного полуцикла (0, 2; 2, 0) вместо
. В табл. 12.27 для исключения запрещенного полуцикла (0, 2; 2, 0) вместо  подставляем
подставляем  ∞. Аналогичная операция выполняется в табл. 12.28 (
∞. Аналогичная операция выполняется в табл. 12.28 (  ∞) и 12.30 (
∞) и 12.30 (  ∞). В остальном вычислительная процедура полностью аналогична вычислительной процедуре решения задачи о назначениях.
∞). В остальном вычислительная процедура полностью аналогична вычислительной процедуре решения задачи о назначениях. k i
k i 6
6 2
2 ∞.
∞. k i
k i 00
00 4
4 k i
k i
 Таблица 12.30
Таблица 12.30 ∞
∞ , которому соответствуют
, которому соответствуют  . Анализ дерева возможных вариантов (рис. 12.3) показывает, что для всех ветвей дерева выполняется условие
. Анализ дерева возможных вариантов (рис. 12.3) показывает, что для всех ветвей дерева выполняется условие  . Значит, полученное решение является оптимальным, и изделия нужно обрабатывать в последовательности 2, 3, 1, 4. Общее время обработки при этом будет Т=47. На рис. 12.4 изображены графики обработки изделий в оптимальной последовательности и в последовательности 1, 2, 3, 4. Неоптимизированному варианту соответствует общее время обработки Т=57. Таким образом, последовательность существенно влияет на время обработки всех изделий.
. Значит, полученное решение является оптимальным, и изделия нужно обрабатывать в последовательности 2, 3, 1, 4. Общее время обработки при этом будет Т=47. На рис. 12.4 изображены графики обработки изделий в оптимальной последовательности и в последовательности 1, 2, 3, 4. Неоптимизированному варианту соответствует общее время обработки Т=57. Таким образом, последовательность существенно влияет на время обработки всех изделий.



