 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Домашняя контрольная работа по дисциплине «Статистика. Часть 1»
Данный раздел содержит типовой вариант домашней контрольной работы с образцом решения всех предложенных задач.
ВАРИАНТ № х
Задача 1 Имеются следующие данные о производственных показателях за отчетный период двух цехов предприятия:
Вычислите для двух цехов вместе: 1. Средний процент выполнения плана выпуска продукции. 2. Средний процент стандартной продукции. Укажите, какой вид средней надо применить для вычисления этих показателей. Решение 1. Исходя из формулы (3.1.2), средний процент выполнения плана выпуска продукции по всем цехам находится по следующей формуле:
Сумма фактического выпуска продукции (
Таким образом: 2. Средний процент стандартной продукции рассчитывается по следующей формуле:
где
Тогда : Для вычисления
Задача 2 В целях изучения урожайности подсолнечника в колхозах области проведено пятипроцентное выборочное обследование 100 га посевов, отобранных в случайном порядке, в результате которого получены следующие данные (выборка бесповторная):
На основе этих данных вычислите: 1. С вероятностью 0.997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средняя урожайность подсолнечника в области. 2. С вероятностью 0.954 предельную ошибку выборочной доли и границы удельного веса посевных площадей области с урожайностью от 15 до 19 центнеров с 1 га. 3. Найти коэффициент вариации и сделать выводы о совокупности. Решение
Таблица 2.1– Расчетная
Среднюю урожайность ( Длина интервала: I = 2 (ц с 1 га). Вариант ряда с максимальной частотой: А = 16 (ц с 1 га). Момент первого порядка:
Следовательно: Далее рассчитаем дисперсию по способу моментов, формулы (3.3.7), (3.3.8): Момент второго порядка -
Расчет средней ошибки средней величины при бесповторном отборе, представлен в формуле (3.4.2):
Предельная ошибка средней при бесповторном отборе находится по формуле (3.4.3). Так как вероятность (Р) составляет 0.997, то критерий доверия (t) равен 3, тогда: D Таким образом, доверительные интервалы для средней генеральной совокупности имеют следующие значения и определяются по формуле (3.4.4):
Вывод: таким образом, с вероятностью (Р) равной 0,997 можно гарантировать, что средняя урожайность подсолнечника в области находится в пределах от 15.12 до 16.29 ц с 1 га. Для определения предельной ошибки выборочной доли и границы удельного веса посевных площадей области с урожайностью от 15 до 19 центнеров с 1 га необходимо определить долю вариантов обладающих данным признаком (
Дисперсия выборочной доли, рассчитанная по данным выборочного наблюдения , формула (3.3.9):
Средняя ошибка доли при бесповторном отборе определяется по формуле (3.4.6):
Предельная ошибка доли при бесповторном отборе рассчитывается по формуле (3.4.7). Так как вероятность (Р) равна 0.954, то критерий доверия (t) составляет 2, тогда: D Таким образом, доверительные интервалы удельного веса посевных площадей области с урожайностью от 15 до 19 центнеров с 1 га имеют следующие значения, см. формулу (3.4.8):
Вывод: таким образом, с вероятностью равной 0,954 можно гарантировать, что границы удельного веса посевных площадей области с урожайностью от 15 до 19 центнеров с 1 га находится в пределах от 50.4% до 69.6%.
Коэффициент вариации определим по формуле (3.3.16):
Вывод: так как рассчитанный коэффициент вариации меньше 33%, то совокупность количественно однородная, а величина средней урожайности подсолнечника на 1 га посева типичная. Задача 3 Производство продукции малым предприятием за полугодие характеризуется следующими данными:
Для анализа динамики производства продукции вычислите: 1. Абсолютные приросты, темпы роста и темпы прироста по месяцам и к январю, абсолютное содержание 1% прироста. Полученные показатели представьте в таблице. 2. Среднемесячное производство продукции. 3. Среднемесячный абсолютный прирост. 4. Среднемесячные темпы роста и прироста. Решение Таблица 3.1 — Расчетная
1. Абсолютный прирост цепной ( Темп роста цепной ( Темп прироста цепной ( При этом, за Абсолютное содержание 1% прироста (А) рассчитывается по формуле (3.5.9). 2. Среднемесячное производство продукции, (3.5.13).
3. Среднемесячный абсолютный прирост, (3.5.18):
4. Среднемесячные темпы роста и прироста, соответственно (3.5.20) и (3.5.22):
Вывод: в целом наблюдается положительная тенденция – увеличение объемов производства продукции малыми предприятиями в среднем на 41.6 т. или на 8,1%. При этом среднемесячное производство продукции составляет 527,8 т. Задача 4 Имеются следующие данные о товарообороте магазина:
Вычислить: индивидуальный и общий индексы цен. Решение Таблица 4.1 — Расчетная
Индивидуальные индексы цен: 1) индексы цен для овощей: 2) индексы цен для фруктов: 3) индексы цен для фруктов: Общий индекс цен рассчитаем по формуле (3.6.11):
Вывод: таким образом, товарооборот магазина за счет общего снижения цен на товарную продукцию сократился на 2 % (100%-98%). Задача 5 Имеются следующие данные:
Определите: 1. Недостающие показатели в таблице. 2. Сводные индексы цен, физического объема реализации и товарооборота. 3. Индексы переменного состава, фиксированного состава и структурных сдвигов. Решение
1. Определим недостающие показатели таблицы с помощью формул (3.6.1) и (3.6.2). Так как Так как Аналогично рассчитываются все остальные неизвестные показатели.
Таблица 5.1 — Расчетная
2. Общий индекс цен рассчитаем по формуле (3.6.5):
Общий индекс физического объема определим по формуле (3.6.6):
Общий индекс товарооборота определим по формуле (3.6.4):
Вывод: товарооборот предприятия вырос в отчетном периоде по сравнению с базисным на 6.1% (106.1% — 100%), это произошло только за счет увеличения объемов продаж в среднем на 16.7%, а общее снижение цен на 9.1% (100% — 90.9%) негативно сказалось на товарообороте трех видов товара.
3. Индекс фиксированного (постоянного) состава рассчитаем по формуле (3.6.13):
Индекс структурных сдвигов рассчитаем по формуле (3.6.14):
Индекс переменного состава определим на основании взаимосвязи индексов, формула (3.6.15):
Вывод: в результате совокупного влияния двух факторов: цены и количества товара, цена реализации сократилась в отчетном периоде по сравнению с базисным на 8.78% (100% — 91.22%), в связи только снижением цен на все виды товаров, стоимость реализации уменьшилась на 9.1%, а в следствие изменения структуры продаж, цена продажи немного увеличилась — на 0.35%.
|



 ,
, ) известна, а для нахождения суммы запланированного выпуска продукции (
) известна, а для нахождения суммы запланированного выпуска продукции (  ) необходимо из формулы (3.1.2) выразить
) необходимо из формулы (3.1.2) выразить  =
=  =
=  =
= 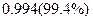 .
. ,
, средний процент стандартной продукции;
средний процент стандартной продукции; количество стандартной продукции.
количество стандартной продукции. =
=  =
=  .
. использовалась формула расчета среднего процента продукции высшего качества (сорта) с помощью средней арифметической взвешенной (3.2.9).
использовалась формула расчета среднего процента продукции высшего качества (сорта) с помощью средней арифметической взвешенной (3.2.9). ) ц с 1 га
) ц с 1 га


 ) рассчитаем по способу моментов, с использованием формул (3.2.7), (3.2.8):
) рассчитаем по способу моментов, с использованием формул (3.2.7), (3.2.8): .
. (ц с 1 га).
(ц с 1 га).





 (ц с 1 га);
(ц с 1 га);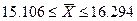 (ц с 1 га).
(ц с 1 га). ), рассчитанную по формуле (3.3.10).
), рассчитанную по формуле (3.3.10).

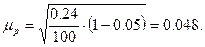




 .
.
 )
) )
)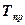 )
)


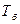

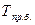
 — значение уровня ряда, взятое за базисное принимается значение уровня ряда 2002 года, т. е.
— значение уровня ряда, взятое за базисное принимается значение уровня ряда 2002 года, т. е.  (т).
(т).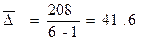 (т.).
(т.). 1,081(108,1%);
1,081(108,1%);







 , то
, то  , следовательно для товара «3» цена за отчетный период рассчитывается:
, следовательно для товара «3» цена за отчетный период рассчитывается: 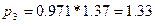 (усл. ед.).
(усл. ед.). , то
, то  , следовательно количество товара «3» за базисный период рассчитывается:
, следовательно количество товара «3» за базисный период рассчитывается:  (усл. ед.).
(усл. ед.). )
) )
) )
) )
) )
)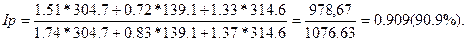




 = 1.0035(100.35%).
= 1.0035(100.35%).