 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ
Статистические показатели Относительный показатель планового задания, (
где
Относительный показатель выполнения плана, (
где
Относительный показатель динамики, (
Взаимосвязь показателей:
Средние величины
Средняя арифметическая, (
где f — веса (частоты или частности) каждого варианта.
Средняя гармоническая, (
где Z = X*f. Средняя геометрическая, (
где П — знак произведения.
Расчет среднего процента выполнения плана,(
Расчет среднего процента продукции высшего качества (сорта),(
где
Расчет среднего процента бракованной продукции (
где
Расчет средней арифметической «способом моментов» для интервальных рядов распределения:
где i — величина интервала; m1 — момент первого порядка.
где
Структурные средние для интервальных рядов распределения: а) мода для интервальных рядов распределения, (
где Хm — начальное значение интервала, содержащего моду; im — величина модального интервала; fm — частота модального интервала; fm-1 — частота интервала, предшествующего модальному; fm+1 — частота интервала, следующего за модальным.
б) медиана для интервальных рядов распределения, (
где Хmе — начальное значение интервала, содержащего медиану; imе — величина медианного интервала;
Sme-1 — кумулятивная частота интервала, предшествующих медианному; fmе — частота медианного интервала. Показатели вариации Размах вариации, (
Среднее линейное отклонение, ( а) для несгруппированных данных:
б) для сгруппированных данных:
Дисперсия, (s2): а) простая дисперсия для несгруппированных данных:
б) взвешенная дисперсия для вариационного ряда, общая дисперсия:
Упрощенные методы расчета дисперсии: а) метод электронно-вычислительного способа расчета:
б) По «способу моментов»:
где m2 — момент второго порядка, определяемый по формуле:
где m1 — момент первого порядка, определяемый по формуле (3.2.14).
Дисперсия альтернативного признака, (
где W — доля единиц, обладающих альтернативным признаком.
где m — количество единиц, обладающих альтернативным признаком; n — численность единиц совокупности.
Среднее квадратическое отклонение, (s ):
Правило сложения дисперсий:
где s2 — общая дисперсия;
d2 — дисперсия групповых средних (межгрупповая) дисперсия.
Средняя из внутригрупповых дисперсий:
где
Внутригрупповые дисперсии:
где
Межгрупповая дисперсия:
где
Коэффициент вариации, (
Коэффициент детерминации, (
Эмпирическое корреляционное отношение, (
Выборочное наблюдение ‑Для средней величины: Средняя ошибка средней при собственно случайном и механическом методах отбора, ( а) повторный отбор:
б) бесповторный отбор:
где n — численность выборочной совокупности; N — численность генеральной совокупности; s
Дисперсия средней (
Предельная ошибка выборочной средней, ( D
где t — коэффициент кратности (доверия), зависит от вероятности (Р), с которой можно гарантировать, что предельная ошибка (D при Р = 0,683 - t = 1; Р = 0,954 - t = 2; Р = 0,997 - t = 3.
Доверительный интервал для средней в генеральной совокупности:
где
‑ Для доли единиц совокупности:
Средняя ошибка доли при собственно случайном и механическом методах отбора, ( а) повторный отбор:
б) бесповторный отбор:
где n — численность выборочной совокупности; N — численность генеральной совокупности; s
Дисперсия выборочной доли
Предельная ошибка выборочной доли ( D
Доверительный интервал для доли единиц в генеральной совокупности:
Ряды динамики Основные показатели анализа ряда динамики: Абсолютный прирост уровня ряда динамики:
где
Темп роста уровня ряда динамики:
Темп прироста уровня ряда динамики, в %:
Или:
Темп прироста уровня ряда динамики, в коэффициентах:
Абсолютное значение 1 % прироста:
Взаимосвязь показателей анализа ряда динамики:
где
‑Основные формулы расчета среднего уровня ряда динамики, (
Для интервальных рядов динамики:
где n — число уровней ряда; t — веса, длительность интервалов времени между смежными датами.
Для моментных рядов динамики:
где
‑Средние показатели ряда динамики. Рассчитываются по интервальным рядам динамики с равными интервалами:
Средний абсолютный прирост, (
Средний темп роста, в коэффициентах:
где П — означает произведение всех цепных темпов роста; Т
Средний темп прироста, в коэффициентах:
Индексы Индивидуальные индексы:
где
Общие индексы (взвешенные агрегатные индексы):
Общие индексы, рассчитанные как средневзвешенные величины из индивидуальных индексов:
Индекс переменного состава:
Индекс постоянного (фиксированного) состава:
Индекс структурных сдвигов:
где
Взаимосвязь индексов:
|



 ):
):
 — запланированный уровень на отчетный период;
— запланированный уровень на отчетный период; — фактически достигнутый уровень за базисный период.
— фактически достигнутый уровень за базисный период. ):
):
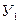 — фактически достигнутый уровень отчетного периода.
— фактически достигнутый уровень отчетного периода. ):
):

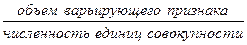 .
.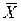 ):
):

 ):
):

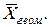 ):
):
 ):
): ;
; ,
, ):
): ;
; ,
, — объем продукции высшего качества (сорта);
— объем продукции высшего качества (сорта); — удельный вес продукции высшего качества в общем объеме фактически выпущенной продукции.
— удельный вес продукции высшего качества в общем объеме фактически выпущенной продукции. ):
): ;
; ,
, — объем бракованной продукции;
— объем бракованной продукции;

 — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой.
— условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой. ):
):
 ):
):
 — сумма частот ряда;
— сумма частот ряда; ):
):
 ):
):



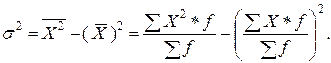


 ):
):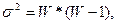



 — средняя из внутригрупповых дисперсий;
— средняя из внутригрупповых дисперсий;
 — групповые дисперсии;
— групповые дисперсии; — численность единиц в i‑ой группе.
— численность единиц в i‑ой группе.
 — групповые средние;
— групповые средние; — варианты внутри групп;
— варианты внутри групп; .
.
 — общая средняя;
— общая средняя;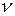 ):
):
 ):
):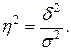
 ):
):

 ):
):

 — дисперсия средней, рассчитанная по данным выборочного наблюдения;
— дисперсия средней, рассчитанная по данным выборочного наблюдения; — доля выборки.
— доля выборки. ) находится с использованием формул (3.3.4-3.3.8), в зависимости от требований, указанных в задании.
) находится с использованием формул (3.3.4-3.3.8), в зависимости от требований, указанных в задании.

 — средняя в выборочной совокупности;
— средняя в выборочной совокупности; — средняя в генеральной совокупности.
— средняя в генеральной совокупности. ):
):

 — дисперсия выборочной доли, рассчитанная по данным выборочного наблюдения;
— дисперсия выборочной доли, рассчитанная по данным выборочного наблюдения; находится с помощью формулы (3.3.9), которая используется для расчета дисперсии альтернативного признака.
находится с помощью формулы (3.3.9), которая используется для расчета дисперсии альтернативного признака.
 .
.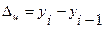 ;
;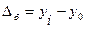 ,
,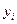 — уровень изучаемого периода;
— уровень изучаемого периода; — уровень предшествующего периода;
— уровень предшествующего периода; — значение уровня ряда, принятое за базисное.
— значение уровня ряда, принятое за базисное.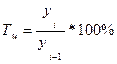 ;
; .
. ;
; .
. ;
; .
. .
. ;
;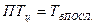 ;
; ,
, — сумма цепных абсолютных приростов;
— сумма цепных абсолютных приростов; — значение базисного абсолютного прироста, стоящего последним в ряду динамики;
— значение базисного абсолютного прироста, стоящего последним в ряду динамики; — произведение всех цепных темпов роста;
— произведение всех цепных темпов роста; — значение базисного темпа роста, стоящего последним в ряду динамики.
— значение базисного темпа роста, стоящего последним в ряду динамики. ):
): ;
; ,
, — абсолютные уровни ряда;
— абсолютные уровни ряда; ,
, ;
; ,
, ):
): .
.
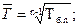

 — значение базисного темпа роста, стоящего
— значение базисного темпа роста, стоящего  ‑ным в ряду динамики;
‑ным в ряду динамики;
 ;
; ;
;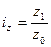 ,
, — объем производства за отчетный и базисный периоды соответственно;
— объем производства за отчетный и базисный периоды соответственно;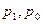 — цена единицы продукции (товара) за отчетный и базисный периоды соответственно;
— цена единицы продукции (товара) за отчетный и базисный периоды соответственно; — себестоимость единицы продукции за отчетный и базисный периоды соответственно.
— себестоимость единицы продукции за отчетный и базисный периоды соответственно. ;
;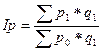 ;
;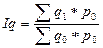 ;
; ;
; ;
; .
.
 ;
; 

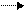
 ;
;
 ;
;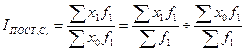 ;
; ,
, — усредненное значение изучаемого признака, рассчитанное по формуле средней арифметической взвешенной, за отчетный и базисный периоды соответственно;
— усредненное значение изучаемого признака, рассчитанное по формуле средней арифметической взвешенной, за отчетный и базисный периоды соответственно; — значение усредняемого показателя за отчетный и базисный периоды соответственно;
— значение усредняемого показателя за отчетный и базисный периоды соответственно; — веса (частоты или частности) каждого значения изучаемого признака за отчетный и базисный периоды соответственно.
— веса (частоты или частности) каждого значения изучаемого признака за отчетный и базисный периоды соответственно. ;
; ;
; .
.