ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задания для самостоятельной работы.
Задание № 1-1.
1. Вычислить выражения:
2. Вычислить i38. 3. Решить систему: (1 + i)z1 + (1 - i)z2 = 1+i, (1 - i)z1 + (1 + i)z2 = 1+3i . 4. Доказать, что комплексное число z является вещественным тогда и только тогда, когда 5. Найти комплексные числа, сопряженные своему квадрату. 6. Найти тригонометрическую форму чисел:
7. Вычислить выражения: 8. Вычислить
Ответы 1а. -15+15i; 5. 1) 0, 2) 1, 3) 1б. 1; 6. Задание № 2-2. 1. Вычислить: 2. Составить таблицу умножения для группы корней 6-ой степени из 1. 3. Выписать все корни из 1 и указать первообразные для степеней 3 и 12. 4. Решить уравнение:
Ответы. 1а. 1б. 1в. 1г. Задание № 3-4.
1. Решить методом Гаусса системы уравнений:
а)
в)
д)
2. Исследовать системы и найти общее решение в зависимости от значений параметров: а)
в) Ответы.
1а. x1 = 1/2, x2 = -2/3, x3 = 2, x4 = -3. 1г. x1 =1, x2 = 2, x3 = 1. 1б. x1 = 1/10(6 - 15x2 - x4 ), 1д. х1 = 7/6x5 - x3 , x2 = 5/6x5 + x3, x3 = 1/5(1 + 4x4). х4 = 1/3x5. 1в. x1 = x2 =0, x3 = x4. 1e. x1 = - 16+x3 + x4 + 5x5, x2 = 23 - 2x3 - 2x4 - 6x5. 2a. l = 8: x3 = -1, x4 = 2 - x1 - 3/2x2, l ¹ 8: x2 = 4 - 2/3x1, x3 = - 1, x4 = 0. 2б. l ¹ 1, -2: x1 = x2 = x3 = 1/ l+2, l = 1: x1 = 1 - x2 - x3 , l = -2: решений нет. 2в. При a = 0, чаях только нулевое решение. 2г.
Задание № 4-5.
1. Вычислить определители:
2. Пользуясь теоремой Крамера, решить системы:
3. Перемножить перестановки в указанном и обратном порядке.
4. Найти перестановку x из равенства Ах = В, где
5. Определить число инверсий в последовательностях: а) 2, 3, 5, 4, 1; б) 6, 3, 1, 2, 5, 4; в) k, k+1, . . . , n, k-1, k-2, . . . , 2, 1. 6. Определить четность перестановок:
7. С каким знаком в определитель 6-го порядка входят произведения:
8. Какие значения должны принимать i и k, чтобы произведение входило в определитель 9-го порядка со знаком “+“ ?, со знаком “-“ ? 9. Пользуясь определением, вычислить определитель:
Ответы
1а. 0. 1б. 0. 1в. -2. 1г. 40. 1д. a3 + b3 + c3 - 3abc. 1е. 0. 2а. x = cosa cosb, y = cosa sinb. 2б. x = 1, y = 2, z = -1. 2в. x1 = 3, x2 = 4, x3 = 5. 3a. 6а. +(четн). 6б. +(четн). 6в. 1/2(n + 1). 7a. +. 7б. +. 8. i = 5, k = 8 -, i = 8, k = 5 +. 9. abcd.
Задание 5-3.
1. Как изменится определитель порядка n, если:
а) его строки записать в обратном порядке ? б) к каждому столбцу, начиная со второго прибавить предыдущий столбец ? в) к каждому столбцу, начиная со второго прибавить все предыдущие столбцы ?
2. Не развертывая определителей, доказать тождество:
3. Вычислить определители:
4. Предложить схему вычисления определителей 3-го порядка, отличающуюся от “правила “треугольников”.
5. Предложить схему вычисления определителей 4-го порядка.
Ответы
1а. Умн. на 3б. 90. 3е. n!. 1б. Не изменится. 3в. 1. 3ж. x1(x2 - a12)(x3 - 1в. Не изменится. 3г. 5. - a23)…(xn - an-1,n). 2. Умн. 2-й столб на yz...
Задание 6-5.
1. Вычислить определители приведением к треугольному виду:
2. Вычислить определители методом рекуррентных соотношений.
3. Вычислить определители методом представления их в виде суммы определителей.
Ответы 1. (-1)n(n-1) 2n. Из каждого столбца, начиная со второго, вычесть предыдущий. 2. 2n+1. 3. n+1. 4. 2n+1 - 1. 5. (-1)n-1 n!. 6. 0. 7. (x - a1)(x - a2)...(x - an). 8. (-1)n-1(n - 1)xn-2 .
Задание № 7-3.
1.Найти вектор х из уравнения а1 + 2а2 + 3а3 + 4х = 0, где а1 = (5, -8, -1, 2), а2 = (2, -1, 4, -3), а3 = (-3, 2, -5, 4). 2.Выяснить, являются ли следующие системы векторов линейно независимыми: а) а1 =(4,-2,6), а2 =(6,-3,9); б) а1 = (2,-3,1), а2 =(3,-1,5), а3 =(1,-4,3). 3.Система векторов а1, а2,...,аk - линейно независима, выяснить, являются ли линейно зависимыми системы векторов: а) b1 = 3а1 + 2а2 + а3 + а4, б) b1 = а1, b2 = 2а1 + 5а2 + 3а3 + 2а4, b2 = а1 + а2, b3 = 3а1 + 4а2 + 2а3 + 3а4. b3 = a1 + a2 + a3, ....... bk = a1 + a2 +...+ аk. 4.Найти все значения l, при которых вектор b линейно выражается через векторы а1, а2: а1 = (3, 4, 2), а2 = (6, 8, 7), b = (9, 12, l) . 5.Найти какой ни будь базис системы векторов и выразить через него остальные векторы системы: а) а1 = (2, 2, 7, -1), а2 = (3, -1, 2, 4), а3 = (3, 5, -13, 11); б) а1 = (2, 1), а2 = (3, 2), а3 = (1, 1), а4 = (2, 3).
Ответы 1. (0, 1, 2, -2). 4. l - любое. 2а. Нет. (л. зав.) 5а. (а1, а2, а3). 2б. Да. (л. нез.) 5б. (a1, a2), a3 = -a1 + a2, 3а. Нет. (л. нез.) a4 = -5a1 + 4a2. 3б. Нет. (л. нез.) Задание № 8-3. 1.Найти ранг матриц с помощью элементарных преобразований:
2.Вычислить ранг матриц: а) 3.Найти ранг матрицы при различных значениях параметра l:
4.Докажите,что если ранг матрицы А не изменяется от приписывания к ней любого столбца матрицы В с тем же числом строк, то он не меняется от приписывания к матрице А всех столбцов матрицы В. Ответы 1a. 3. 1б. 3. 1в. 3. 2а. 2. 3. 2 при l = 0, 3 при l ¹ 0. 2б. 5. 2в. 3. 4. Док-во. Задание 9-4. 1.Перемножить матрицы:
2. Вычислить: а) 3.Решить уравнения: а) 4.Найти обратную матрицу к матрице: а) 5.Найти все матрицы второго порядка, квадраты которых равны нулевой матрице. 6.Найти общее решение и фундаментальную систему решений сис- тем уравнений: а) х1 + х2 + х3 + х4 + х5 = 0, б) х1 + х2 = 0, 3х1 + 2х2 + х3 + х4 - 3х5 = 0, х3 + х4 = 0, х2 + 2х3 + 2х4 + 6х5 = 0, х2 + ix3 = 0. 5х1 + 4х2 + 3х3 + 3х4 - х5 = 0;
Ответы.
1а. 1б. 1в. 1г. 6a. ФСР: (1, -2, 1, 0, 0), (1, -2, 0, 1, 0), (5, -6, 0, 0, 1); Общ. реш.: x1, = C1 + C2 + 5C3, x2 = -2C1 - 2C2- 6C3, x3 = C1, x4 = C2, x5 = C3. 6б. ФСР: (-i, i, -1, 1); Общ. реш.: x1 = -Сi, x2 = Ci, x3 = -C, x4 = C. Задание 10-2.
1.Выполнить деление с остатком многочленов f(x) на g(x): а) f(x) = x3 - 3x2 - x - 1, g(x) = 3x2 - 2x + 1; б) f(x) = 2x5 - 5x3 + 8x, g(x) = x + 3. 2.При каком условии полином х4 + px2 + q делится на полином вида х2 + mx + 1? 3.Подобрать такие многочлены u(x) и v(x), что f(x)u(x) + g(x)v(x) = 1: f(x) = x4 - x3 - 4x2 + 4x + 1, g(x) = x2 - x - 1. 4.Найти наибольший общий делитель многочленов: а) х6 + 2х4 - 4х3 - 3х2 + 8х - 5 и х5 + х2 - х + 1, б) х4 - 4х3 + 1 и х3 - 3х2 + 1. 5.Найти наибольший общий делитель полинома и его производной: f(x)=(x-1)3(x+1)2(x-3). 6.Пользуясь алгоритмом Евклида, подобрать полиномы М1(х) и М2(х) так, чтобы f1(x)M2(x) + f2(x)M1(x) = d(x), где d(x) - наибольший общий делитель f1(x) и f2(x): f1(x) = x5 + 3x4 + x3 + x2 + 3x + 1, f2(x) = x4 + 2x3 + x + 2 . Ответы .
1а. 1/9(3x-7), -1/9(26x+2). 4a. х3 - x + 1. 1б. (2x4 - 6x3 + 13x2 - 39x + 4б. x2 - 2 + 125)(x + 3) - 375. 5. (x-1)2 (x + 1). 2. 1) q = p - 1, m=0, 6. -f1(x) + (x + 1)f2(x) = x3 + 1. 2) q = 1, m = 3. U(x) = -x - 1, V(x) = x3 + x2 - 3x - 2. Задание № 11-1
Разложить на неприводимые множители над полем С или полем вещественных чисел многочлены: 1. х6 - 15х4 + 8х3 + 51х2 - 72х + 27, 2. х 3 - 6х2 + 11х - 6, 3. х12 + х8 + х4 + 1, 5 0 4. х4 + 4.
Ответы 1. (x - 1)3(x + 3)3(x - 3). 2. (x - 1)(x - 2)(x - 3). 3. (x2 + x -x 4. (x2+ 2x + 2)(x2 - 2x + 2).
Задание № 12-2. 1.Пользуясь схемой Горнера, разложить полином f(x) по степеням х - х0: a) f(x) = x5, x0 = 1, б) f(x) = 2x5 - 5x3 - 8x, x0 = -3. 2.Отделить кратные множители полиномов: a) f(x) = x5 - 10x3 - 20x2 - 15x - 4, b) f(x) = x8 + 2x7 + 5x6 + 6x5 + 8x4 + 6x3 + 5x2 + 2x + 1. 3.Построить полином наименьшей степени по данной таблице
f(x) 6 5 0 3 2
Ответы.
1a. (x - 1)5 + 5(x - 1)4 + 10(x - 1)3 + 10(x - 1)2 + 5(x - 1) + 1. 1б. f(x) = (x + 3)(2x4 - 6x3 + 13x2 - 39x + 109) - 327, f(x0) = -327. 2а. (x + 1)4(x - 4). 2б. (x4 + x3 + 2x2 + x + 1)2. 3. f(x) = -x4+ 4x3 - x2 - 7x + 5. Задание № 13 - 4.
1. Построить полином наименьшей степени с действительными коэффициентами, с корнями: а) 3 (двойной корень), -2, -4 (простые корни); б) 1 (двойной корень), 2, 3, 1+ i (простые корни). 2. Найти соотношение между коэффициентами кубичного уравнения х3 + pх2 + qх + r , при котором один корень равен сумме двух других. 3. Найти х так, чтобы |f(х)| < |f(0)|, где f(х) = х5 - 3iх3 + 4. 4. Найти соотношение между коэффициентами уравнения х4 + ах3 + bх2 + сх + d = 0, при котором сумма двух корней равна сумме двух других корней.
Ответы. 1a. x4 - 19x2 - 6x + 72. 1б. (x - 1)2(x - 2)(x - 3)(x2 - 2x + 2) = x6 - 9x5 + 33x4 - 65x3 + 74x2 - - 46x + 12. 2. Один из корней = -p/2, соотношение 8r = 4рq - p3. 3. x = ri, 0 < r < 4. a3 - 4ab + 8c = 0. Задание № 14-5.
1.Составить ряд Штурма и отделить корни многочленов: а) х3 + х - 5, б) х4 - 12х2 - 16х - 4, в) х4 - х3 + х2 - х - 1. 2.Определить все многочлены с коэффициентами ±1, имеющие только вещественные корни. 3.Ограничить сверху и снизу вещественные корни многочлена: х4 - 4х3 + 7х2 - 8х + 3. 4.Определить число вещественных корней уравнения: х5 - 5ах3 + 5а2х + 2b = 0. 5.Вычислить с точностью до 0,0001 вещественные корни уравнения х3 - 3х2 - 4х + 1 = 0. 6.Вычислить с точностью до 0,0001 корень уравнения 3х4 + 4х3 + х2 + х - 3 = 0, содержащийся в интервале (0,1). Ответы.
1а. 1 вещ. корень в интервале: (1, 2). 1б. 4 вещ. корня в интервалах: (-3, -2), (-2, -1), (-1, 0), (4, 5). 1в. f = x4 - x3 + x2 - x - 1, f1 = 4x3 - 3x2 + 2x - 1, f2 = -5x2 + 10x + 17, f3 = -8x - 5, f4 = -1. 2 вещ. корня в интервалах: (1, 2), (-1, 0). 2. x3 + x2 - x - 1, x2 ± x - 1, x ± 1. 3. 0 < xi < 3. 4. Ряд Штурма: f = x5 - 5ax3 + 5a2x + 2b, f1 = x4 - 3ax2 + a2, f2 = ax3 - 2a2x - b, f3 = a(a2x2 - bx - a3), f4 = a(a5 - b2)x, f5 = 1. Если a5 - b2 > 0, то a > 0, все старшие коэф. > 0, все 5 корней f-веществ., если a5 - b2 < 0, то в зависимости от знака а распределение знаков выглядит: f f1 f2 f3 f4 f5 a>0 -¥ - + - + + + +¥ + + + + - + 5. 3,9489, 0,2172, -1,1660. a<0 -¥ - + + - - + +¥ + + - - + + 6. 0,6180.
ЗАДАНИЕ № 15-3.
1.Ассоциативна ли операция Ä на множестве М, если а) М = N, х Ä y = 2xy; б) М = Z, x Ä y = x - y; в) М = Z, х Ä y = x2 + y2. 2.Определены ли на множествах N, Z, Q, 2Z, 2Z+1, R, R+ следующие операции. Какие из операций обладают свойствами ассоциативности, коммутативности ? а) a Ä = ab; в) a Ä b = (а + b)/2; б) a Ä b = a/b; г) a Ä b = 3.Какие из указанных множеств с операциями являются группами: а) (nZ, +), где n Î N; б) ( -1, 1, ×); в) множество степеней числа а Î R (а ¹ 0) с целыми показателями относительно умножения; г) множество невырожденных матриц относительно сложения; д) множество невырожденных матриц относительно умножения; е) множество матриц с фиксированным определителем d относительно умножения; ж) множество R+, если операция определена так: а Ä b = a2b2; з) множество действительных многочленов степени £ n (включая нуль) относительно сложения; и) чётные перестановки чисел 1, 2,..., n относительно умножения; к) матрицы порядка n с целыми элементами относительно умножения.
Ответы . 1а. Да. 1б. Нет. 1в. Да. 2а. Ком., асс. 2в. Ком. 2г. Ком. 3а. Да. 3б. Да. 3в. Да. . 3г. Нет. 3д. Да. 3е. Да при d = 1. 3ж. Нет. 3з. Да. 3и. Да. 3к. Нет.
Задание № 16-1.
1.Найти порядок элемента в группе: а)
2.Доказать, что множество всех корней n-ой степени из 1 образует подгруппу в мультипликативной группе всех комплексных чисел, отличных от 0. Составить таблицы умножения для группы корней n-ой степени из 1 для n = 3, 4, 6. 3.Какие из следующих числовых множеств образует кольцо относительно обычных операций сложения и умножения: а) множество Z; б) множество всевозможных сумм вида a1z1 + a2z2 +...+ anzn, где аi Î R, zi - комплексные корни из 1? 4.Какие из следующих множеств матриц образуют кольца: а) г) множество вещественных симметрических матриц порядка n; д) множество вещественных матриц вида
5.Доказать, что следующие множества являются полями: а) Q; б) 6.Показать, что матрицы вида
Ответы. 1а. 5; 1б. 3; 2. Док-во. 3а. Да. 3б. Да. 4а. Да. 4б. Да. 4в. Да. 4г. Нет. 4д. Нет.
ЗАДАНИЕ № 17-4.
1.Какие значения может принимать определитель: а) ортогональной матрицы, б) унитарной матрицы ? 2.При каком условии произведение двух эрмитовых или косоэрмитовых матриц является эрмитовой матрицей ? 3.Доказать, что всякая нижняя нильтреугольная матрица нильпотентна. 4.Как изменится обратная матрица А-1, если в данной матрице: а) переставить i-ю и j-ю строки ?; б) i-ю строку умножить на число с ¹ 0?; в) к i-ой строке прибавить j-тую, умноженную на число с, или совершить указанные действия со столбцами? 5.Показать, что для любой матрицы 6.Доказать, что определитель унитарной матрицы по модулю равен единице. 7.Квадратная матрица Р идемпотентна, если Р2 = Р. Показать, что если Р идемпотентна, то J = 2P - E инволютивна и наоборот, если J - инволютивна, то Р = 1/2(J + E) идемпотентна. 8.Найти Аn для всех целых положительных чисел n: а) А = Ответы.
1. a),б) ±1. 5. Доказательство. 2. Если матрицы 6. Доказательство. перестановочны. 7. Доказательство. 3. Нет ответа. 8a. 2. а) поменяются местами i-тый и j-тый столбцы, 8б. A при n четн, Е при неч. б) i-тый столбец умн. на 1/с, в) из j-того столбца вычтется i-тый, умн. на с. Со строками наоборот. ЗАДАНИЕ № 18-3 . 1.Выяснить, являются ли подобными между собой матрицы: А = 2.Найти минимальный многочлен матрицы 3.Привести к нормальной диагональной форме путём элементарных преобразований следующие матрицы: а) 4.Привести к нормальной диагональной форме при помощи элементарных преобразований матрицы: а) б) Ответы.
1. Да. 4а. 2. (t - 2)3. 4б. 3а. с-произвед. старших коэффициентов.
3б. ЗАДАНИЕ № 19-2.
1.Выяснить, являются ли подобными между собой матрицы А = 2.Найти минимальный многочлен нулевой матрицы. 3.Привести к нормальной диагональной форме путём элементарных преобразований следующие матрицы: а) 4.Привести к нормальной диагональной форме при помощи делителей миноров следующие матрицы: а) Ответы. 1. Да. 4а. 2. t. 3а. 3б. ЗАДАНИЕ № 20-1. Найти жорданову форму матриц: 1)
4) Ответы.
1) Задание № 21-5. 1.В векторном пространстве V над полем С определено новое умножение векторов на комплексные числа по правилу:
2.Проверьте, выполняются ли аксиомы векторного пространства для множества всех векторов плоскости с операциями сложения и умножения на рациональные числа. 3.Является ли множество всех арифметических n-мерных векторов (х1, х2,...,хn) в Fn векторным пространством над полем F, если: а) х1 = 1, б) х12 -хn2 = 0 ? 4.Является ли векторным пространством над полем рациональных чисел множество чисел вида а + bi, a, b - действительные неотрицательные ? 5.Установите изоморфизм между пространством многочленов степени £ n с арифметическим векторным пространством Rn+1. 6.При каких a система векторов (1, 2, 3), (3, 2, 1), (1, 1, 1+ a) образует базис арифметического векторного пространства над полем R ? Ответы1 Док-во. 2 Да. 3а Нет. 3б Нет. 4 Нет. 5 Док-во. 6 a¹0 Задание № 22-4. 1.Доказать, что каждая из двух заданных систем векторов S и S1 является базисом. Найти матрицу перехода от S к S1. S = <(1, 2, 1), (2, 3, 3), (3, 8, 2)>; S1 = <(3, 5, 8), (5, 14, 13), (1, 9, 2)>. 2.Как изменится матрица перехода от одного базиса к другому, если поменять местами два вектора первого базиса ? 3.Является ли подпространством соответствующего векторного пространства совокупность многочленов с коэффициентами из некоторого поля F, не содержащих четных степеней переменной х ? 4.Образуют ли подпространство в пространстве матриц Мn(F) вырожденные матрицы порядка n над полем F ? 5.Найти базисы суммы и пересечения линейных оболочек: А = <(1, 2, 1), (1, 1, -1), (1, 3, 3)>; B = <(1, 2, 2), (2, 3, -1), (1, 1, -3)>. 6.Найти базисы суммы и пересечения линейных оболочек: а) А = <(1, 2, 1, -1), (2, 3, 1, 0), (1, 2, 2, -3)>, B = <(1, 1, 1, 1), (1, 0, 1, -1), (1, 3, 0, -4)>; b) A = <(1, 0, 1, 2), (1, 1, 0, 1), (1, 1, 1, 0)>; B = <(3, 2, 2, 3), (2, 1, 2, 2)>. 7.Найти систему линейных уравнений, задающих линейную оболочку системы векторов: А = <(1, -1, 1, -1, 1), (1, 1, 0, 0, 3), (3, 1, 1, -1, 7), (0, 2, -1, 1, 2)>.
Ответы.
1. x1 = -27x'1 - 71x'2 - 41x'3; 5. (a1, a2, b1); (3, 5, 1). x2 = 9x'1 + 20x'2 + 9x'3; 6a. a1, a2, a3, b2; базис пересеч. x3 = 4x'1 + 12x'2 + 8x'3 . b1 = -2a1 + a2 + a3, b2 = 5a1 - a2 - 2a3. 2. Поменяются местами 6б. UÉV. 2 строки. 7. x1 - x2 - 2x3 = 0; 3. Да. x1 - x2 + 2x2 = 0 4. Нет, т.к. сумма вырожд. 2x1 + x2 - x5 = 0. матр. может быть невырожд.
ЗАДАНИЕ № 23 -5.
1.Выяснить, какие из следующих преобразований j(х) являются линейными. В случае линейности найти матрицу данного преобразования: a) j(х) = (x1, x1, 0); б) j(х) = (kx1, kx2, kx3); в) j(х) = (x1 + 1, x2 + 2, x3 + 3). 2.Найти все векторы пространства Rn, переходящие в вектор b пространства Rm при линейном отображении jA: Rn ® Rm, заданном матрицей А: a) A = Ответы.
ЗАДАНИЕ 24-1.
1. Является ли линейным отображение х ® а (а- фиксированный вектор)? 2. Найти матрицу линейного преобразования трёхмерного пространства, переводящего векторы а1, а2, а3 соответственно в b1, b2, b3: а1 = (2, 3, 5), b1 = (1, 1, 1), а2 = (0, 1, 2), b2 = (1, 1, -1), а3 = (1, 0, 0), b3 = (2, 1, 2). 3. Какие из следующих преобразований являются линейными? В случае линейности найти матрицу, ранг и дефект преобразования: а) j(х1, х2, х3) = (х1 + х2, х2 + х3, х3 + х1), б) j(х1, х2 , х3) = (х1 + 1, х2 + 2, х3 + 3). 4. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей
5. Найти все подпространства пространства R3, инвариантные относительно линейного преобразования, заданного матрицей:
Ответы. 1. При а = 0 . 2. 3б. Не является. 4. l1 = l2 = l3 = 0, собсв. векторы: с(1, 1, -1), с ¹ 0. 5. Прямая с базисным вектором а1 = (2, 2, -1); Любая прямая плоскости L с базисными векторами a2 = (1, 1, 0), a3 = (1, 0, -1), т.е. плоскость x1 - x2 + x3 = 0; Любая плоскость, проходящая через а, все пространство и нулевое подпространство. Задания для самостоятельной работы.
1. При каком значении l линейное преобразование трехмерного пространства, заданное преобразованием координат x1 = -2x + y + z, y1 = x - 2y + z, z1 = x + y + lz, не имеет обратного? 2. Найти собственные значения и собственные векторы линейных преобразований, заданных в некотором базисе матрицами:
3. Доказать, что если линейное преобразование j2 имеет собственное значение l2, то одно из чисел l и -l является собственным значением преобразования j. 4. Доказать, что если А и В – квадратные матрицы одинакового порядка, то матрицы АВ и ВА имеют совпадающие характеристические многочлены. 5. В пространстве многочленов степени не выше k задано линейное преобразование j. Найти минимальный многочлен этого преобразования, его собственные значения, собственные векторы, ядро и все инвариантные подпространства:
а) k = 2, b) k = 3, c) k = 2,
6. В пространстве симметрических матриц второго порядка линейное преобразование задано следующим образом:
Х – любая симметрическая матрица второго порядка. Найти минимальный многочлен этого преобразования, его собственные значения, собственные векторы, ядро и все инвариантные подпространства. 7. В пространстве квадратных матриц второго порядка с элементами из поля вещественных чисел линейное преобразование задано следующим: 8. В пространстве квадратных матриц второго порядка с элементами из поля вещественных чисел задано линейное преобразование j. Найти минимальный многочлен этого преобразования, его собственные значения, собственные векторы, ядро и все инвариантные подпространства:
а) b) c)
9. При каких значениях a число 0 является собственным значением преобразования j, заданного матрицей А? При найденном a определить совокупность собственных векторов преобразования.
10. При каких значениях a число 2 является собственным значением преобразования j, заданного матрицей А? При найденном a определить совокупность собственных векторов преобразования.
11. При каких значениях a, b, g числа 1, 2, 3 будут являться собственными значениями преобразования j, заданного матрицей А? При найденных a, b, g определить совокупность собственных векторов преобразования.
12. Доказать, что линейное подпространство, натянутое на любую систему собственных векторов преобразования j, инвариантно относительно j. 13. Доказать, что любое подпространство, инвариантное относительно линейного преобразования j, будет инвариантно и относительно обратного преобразования j-1. 14. Найти все подпространства трехмерного пространства, инвариантные одновременно относительно двух линейных преобразований, заданных матрицами:
Ответы.
1. При l = -2. 2. а) l1,2 = 1: с1(2, 1, 0) + с2(1, 0, -1); l3 = -1: с(3, 5, 6), сi¹0 одновременно. b) l1 = 1: c(1, 2, 1); l2 = 2 + 3i: c(3 - 3i, 5 - 3i, 4); l3 = 2 - 3i: c(3 + 3i, 5 + 3i, 4), c ¹ 0. c) l = 2, c1(1, 1, 0, 1) + c2(0, 0, 1, 1). 3. Указание: рассмотреть 5.a) l1,2 = 0: с1(1, 0,- 4) + с2(0, 1, 0); l3 = 1, с3(0, 0, 1); fmin = t2 - t. b) l1,2,3 = 0: c1(0, 0, 1, 0) + c2(0, -1, 0, 4); l4 = 1: c3(0, 0, 0, 1); fmin = t3 - t2. c) l1,2 = 0: c1(0, 1, - 2), l3 = 1: c2(0, 0, 1); fmin = t3 - t2. 6. l1,2,3 = 2, c(1, 0, 0), fmin = (t - 2)3. 7. l1 = 0: c1(0, -1, 1, 0); l2,3,4 = 2: c2(1, 0, 0, 0) + c3(0, 1, 1, 0) + c4(0, 0, 0, 1), fmin = t2 - 2t. 8. a) l1,2,3,4 = 2, c1(1, 0, 0, 0) + c2(0, 1, -1/2, 0), fmin = (t - 2)3. b) l1,2,3,4 = 2, c1(1, 1, 0, 0) + c2(2, 0, 1, 1), fmin = (t - 2)3. c) l1,2,3,4 = 1, c1(-1, 1, 0, 0) + c2(-1, 0, -1, 1), fmin = (t - 1)3. 9. a1 = -3, a2 = 1, a) c(1, 0, 1), b) c(0, 1, 1), c) c1(-1, 1, 0) + c2(1, 0, 1). 10. a = 0, c1(1, -2, 0) + c2(0, 0, 1). 11. a = 5, b = -3, g = 2, c1(1, 2, 1), c2(3, 1, 0), c3(1/2, 1, 1). 14. < (1, -2, 1) >; < (1, 1, 1), (1, 2, 3) >, нулевое и все пр-во. |








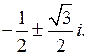 7. a) (-2)30, b) -64.
7. a) (-2)30, b) -64. 8. a2 - ab + b2.
8. a2 - ab + b2.


 3. № 1, 2, №1, 5, 7, 11.
3. № 1, 2, №1, 5, 7, 11.
 . 4.
. 4. 

 б)
б) 
 г)
г) 
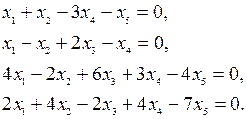 е)
е) 
 б)
б) 
 г)
г) 
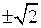 реш. зависит от одного параметра. В других слу-
реш. зависит от одного параметра. В других слу-
 , l = 1: реш. зависит от 3-х парам., l = -3: решений нет.
, l = 1: реш. зависит от 3-х парам., l = -3: решений нет.

 .
.

 .
.


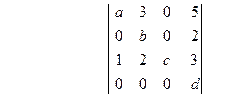 .
. 3б.
3б.  3в.
3в.  4.
4.  5a. 5. 5б. 8. 5в. (k - 1)(n - k) + 1/2(k - 1)(k - 2).
5a. 5. 5б. 8. 5в. (k - 1)(n - k) + 1/2(k - 1)(k - 2).


 . 3а. 18. 3д. x2z2 .
. 3а. 18. 3д. x2z2 .




 б)
б)  в)
в) 
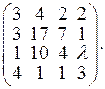


 б)
б)  в)f(x)=x2 - 2x + 1, x =
в)f(x)=x2 - 2x + 1, x = 
 б)
б) 
 б)
б)  в)
в) 
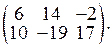 2а.
2а.  3а.
3а. 
 2б.
2б.  3б. Реш. нет.
3б. Реш. нет.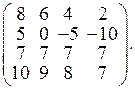 2в.
2в.  4а.
4а.  4б.
4б. 
 4в.
4в. 
 x - 1.
x - 1. .
. + 1)(x2 -
+ 1)(x2 - + 1)(x2 - x
+ 1)(x2 - x  значений: x -1 0 1 2 3
значений: x -1 0 1 2 3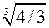 .
. .
.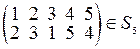 ; б)
; б) 
 ; б)
; б)  ; в)
; в)  .
.
 .
.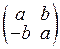 , где а, b Î R, образуют поле, изоморфное полю комплексных чисел.
, где а, b Î R, образуют поле, изоморфное полю комплексных чисел. матрица А=
матрица А=  является сим- метрической.
является сим- метрической. б) А =
б) А = 

 В =
В = 

 б)
б) 

 где f(
где f(  ) и g(
) и g(  где P = (
где P = ( 
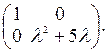 где d(l) = НОД{f(l),g(l)},
где d(l) = НОД{f(l),g(l)},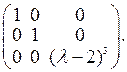
 В =
В = 
 б)
б) 
 б)
б) 

 4б.
4б. 

 ; 2)
; 2)  ; 3)
; 3) 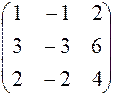 ;
; ; 5)
; 5)  ; 6)
; 6)  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;5)
;5)  ; 6)
; 6)  .
. Ä х =
Ä х =  х (а - число, х - вектор). Доказать, что относительно операций "+" и "Ä" V является векторным пространством.
х (а - число, х - вектор). Доказать, что относительно операций "+" и "Ä" V является векторным пространством. b =
b =  b) A =
b) A =  b =
b = 
 2а.
2а. 
 2б.
2б. 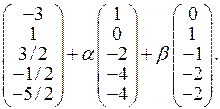


 3a.
3a.  r = 3, def = 0.
r = 3, def = 0.


 где
где  ,
, , где Х Î Мn(R). Найти минимальный многочлен этого преобразования, его собственные значения, собственные векторы, ядро и все инвариантные подпространства.
, где Х Î Мn(R). Найти минимальный многочлен этого преобразования, его собственные значения, собственные векторы, ядро и все инвариантные подпространства.





 и
и