 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Комплексные задачи на энергию и импульс.
16.1. Пуля, летящая горизонтально со скоростью vo = 400 м/с, попадает в брусок, подвешенный на нити длиной l = 4 м, и застревает в нем. Определить угол a, на который отклонится брусок, если масса пули m = 20 г, а масса бруска M = 5 кг. [ 16.2. Тело массой M под действием пружин совершает колебания с амплитудой Ao на гладком горизонтальном столе. В тот момент, когда тело проходит положение равновесия, на него сверху падает и прилипает к нему кусок пластилина массой m. Чему будет равна амплитуда колебаний? [
[ 16.4. Из духового ружья стреляют в спичечный коробок, лежащий на расстоянии l = 30 см от края стола. Пуля массой m = 1 г, летящая горизонтально со скоростью vo = 150 м/с, пробивает коробок и вылетает из него со скоростью vo/2. Масса коробка 50 г. При каких значениях коэффициента трения m между коробком и столом коробок упадет со стола? [ 16.5. Орудие, масса ствола которого M = 400 кг, стреляет в горизонтальном направлении. Масса снаряда m = 8 кг, его начальная скорость vo = 1000 м/с. При выстреле ствол откатывается на S = 50 см. определить среднее значение силы торможения, развивающейся в противооткатном устройстве орудия. [ 16.6. Шарик массой m = 10 г прикреплен к неподвижным стенкам тремя пружинами, слева двумя параллельными пружинами с жесткостью k = 0,375 Н/м, справа – одной с жесткостью k1 = 0,25 Н/м. Шарик может двигаться только вдоль горизонтальной оси. Пружины невесомы и в положении равновесия не напряжены. Шарику сообщают скорость vo = 10 м/с. Найти амплитуду колебаний шарика. Силу тяжести шарика не учитывать. [ 16.7. От удара копра массой m = 50 кг, падающего с высоты H = 5 м, свая массой M = 200 кг погружается в грунт на глубину l = 20 см. Определить силу сопротивления грунта, считая ее постоянной. Удар копра о сваю абсолютно упругий. [
16.9. Космический корабль массой M = 12 т движется вокруг Луны по круговой орбите на высоте h = 100 км. Для перехода на орбиту прилунения на короткое время включается двигатель торможения. Скорость вылетающих из сопла ракеты газов u = 104 м/с. Радиус Луны RЛ = 1700 км, ускорение свободного падения у поверхности Луны gл = =1,7 м/с2. Какую массу топлива m необходимо израсходовать для того, чтобы при включении тормозного двигателя в точке A траектории корабль опустился на Луну в точке B (рис. 16.2). [ 16.10. Два одинаковых маленьких шарика соединены невесомым жестким стержнем длиной l = 60 см. Стержень стоит вертикально вплотную в вертикальной плоскости. При смещении нижнего шарика вправо на малое расстояние система из шариков приходит в движение. Найти скорость нижнего шарика v в момент времени, когда верхний шарик находится на высоте h = 40 см над горизонтальной плоскостью. Считать, что при движении шарики не отрываются от плоскостей, трением пренебречь. [ 16.11. Вдоль гладкой наклонной плоскости, составляющей с горизонтом угол a = 0,01 рад, с начальной скоростью vo = 0,5 м/с, направленной вверх, пускают брусок, который через время t = 2 c упруго ударяется о стенку, движущуюся вдоль наклонной плоскости вниз со скоростью u = 0,1 м/с. Через какое время t после удара о стенку брусок вернется в исходное положение? Трением бруска о наклонную плоскость пренебречь, принять sina = a. [ 16.12. Брусок массой m1 = 4 г соскальзывает без начальной скорости с высоты h = 10 м по наклонной плоскости. Другой брусок массой m2 = 2 г движется по этой плоскости от основания вверх с начальной скоростью vo = 10 м/с. Бруски начинают движение одновременно. На некоторой высоте бруски сталкиваются, после чего движутся как единое тело. Определить скорость v этого тела у основания наклонной плоскости. Трение брусков о плоскость не учитывать. [ 16.13. Шар массой 4 кг, имевший скорость 5 м/с, сталкивается с покоящимся шаром такой же массы. После абсолютно неупругого удара шары движутся вместе с одинаковыми скоростями. Сколько теплоты выделилось при столкновении? [25] 16.14. Движущееся тело сталкивается с неподвижным телом, после чего они движутся вместе со скоростью, которая в 4 раза меньше скорости первоначально движущегося тела. Какая часть (в процентах) кинетической энергии движущегося тела перешла в тепло? [75] 16.15. Горизонтально летящая пуля попадает в неподвижный шар из пенопласта с массой в 5 раз большей, чем у пули, и пробивает его по диаметру. После вылета из шара скорость пули стала в 2 раза меньше первоначальной. Сколько процентов первоначальной энергии пули перешло при этом в тепло? [70] 16.16. Тележка массой 50 кг движется со скоростью 2 м/с по гладкой горизонтальной поверхности. На тележку с высоты 20 см падает груз массой 50 кг и остается на ней. Найдите количество выделившейся теплоты. [150] 16.17. Высунувшись из окна поезда, идущего со скоростью 72 км/ч, человек бросает вперед по ходу поезда камень массой 100 г. Какую работу совершил над камнем человек, если начальная скорость камня направлена горизонтально и равна 30 м/с относительно земли? [5] 16.18. Брусок массой 90 г лежит на гладком полу и соединен с вертикальной стенкой недеформированной пружиной. Ось пружины горизонтальна, жесткость пружины 4 кН/м. В бруске застревает пуля массой 10 г, скорость которой равна 100 м/с и параллельна оси пружины. Чему равна максимальная деформация пружины в (см)? [5] 16.19. Брусок массой 490 г лежит на горизонтальной плоскости и соединен с вертикальной стеной недеформированной пружиной. Ось пружины горизонтальна, жесткость пружины 180 Н/м. В бруске застревает пуля массой 10 г, скорость которой параллельна оси пружины, в результате чего пружина сжимается на 10 см. Чему равна начальная скорость пули? Коэффициент трения между бруском и телом 0,2. [100 м/с] 16.20. В шар массой 440 г, висящий на легком стержне длиной 40 см, попадает и застревает горизонтально летящая пуля массой 10 г. При какой минимальной скорости пули шар после этого совершит полный оборот в вертикальной плоскости? [180 м/с] 16.21. В шар массой 250 г, висящий на нити длиной 50 см, попадает и застревает в нем горизонтально летящая пуля массой 10 г. При какой минимальной скорости пули шар после этого сделает полный оборот в вертикальной плоскости? [130 м/с] 16.22. Небольшое тело массой 0,99 кг лежит на вершине гладкой полусферы радиусом 1 м. В тело попадает пуля массой 0,01 кг, летящая горизонтально со скоростью 200 м/с, и застревает в нем. Пренебрегая смещением тела за время удара, определите высоту (в см), на которой оно оторвется от поверхности полусферы. [80] 16.23. Два упругих шара с массами 200 г и 100 г подвешены рядом так, что их центры находятся на одном уровне. Первый шар отклоняют так, что он поднимается на высоту 18 см, и отпускают. На какую высоту поднимется каждый из шаров после удара? [2 см; 32 см] 16.24. Подъемный кран опускает контейнер массы т на медленно проезжающую со скоростью u железнодорожную платформу. Трос сразу отцепляется. Контейнер скользит по платформе и останавливается, оставив след длины L. Определите коэффициент трения между ящиком и платформой, если трением качения можно пренебречь. Масса платформы М. [ 16.25. Два одинаковых шара движутся со скоростями v1 и v2 вдоль одной прямой. Найдите их скорости u1 и u2 после упругого удара. [u1 = v2; u2 = v1] 16.26. Когда бильярдный шар налетает на другой такой же неподвижный шар, эти шары разлетаются всегда под одним и тем же углом, если удар был нецентральным. Каков этот угол? Столкновение бильярдных шаров можно считать упругим. [90o] 16.27. Два железнодорожных вагона с массами m1 и m2 медленно движутся в одну сторону со скоростями u1 и u2. Вагоны сталкиваются, и пружины буферов расталкивают их так, что удар можно считать упругим. Какова максимальная энергия упругой деформации пружин? [ 16.28. Шар массы m, движущийся со скоростью u, налетел на покоящийся шар массы т/2 и после упругого удара изменил направление своего движения на угол 30°. С какими скоростями движутся шары после удара? [ 16.29. Обезьяна качалась на длинной тонкой лиане, причем максимальный угол отклонения лианы от вертикали был равен a. Когда обезьяна находилась в нижней точке траектории, лиана случайно зацепилась серединой за сук. Каким будет теперь максимальный угол отклонения лианы от вертикали, если a < 60°? Что изменится, если 60° < a < 90°? [ 16.30. Санки съезжают с горы, длина основания которой 5 м, а высота 2 м, и проезжают до остановки еще 35 м по горизонтальной площадке. Найдите коэффициент трения, считая его одинаковым на всем пути. Переход склона горы в горизонтальную поверхность считайте плавным. [0,05] 16.31. Легкий теннисный мячик ударили ногой, и он полетел в направлении движения ноги. Какую скорость приобрел мячик, если скорость движения ноги при ударе 10 м/с? [20 м/с] 16.32. За счет чего увеличивается потенциальная энергия поднимающегося воздушного шара? 16.33.Камень массой 10 кг поднимают на высоту 10 м, прикладывая постоянную силу 200 Н. Какую работу А при этом совершают? Чему равно изменение потенциальной энергии? Как согласуются полученные ответы с законом сохранения энергии? [2 кДж; 0,98 кДж] 16.34. Санки массой 20 кг поднимают по гладкому склону на высоту 2,5 м, прикладывая силу 300 Н, направленную вдоль склона. Санки движутся с ускорением 3 м/с2. Какая работа А совершается при подъеме? Чему равно изменение потенциальной энергии санок? Чему равна кинетическая энергия санок на вершине горы? [612,5 Дж; 490 Дж; 122,5 Дж] 16.35. Автомобиль может удерживаться с помощью тормозов на участке горной дороги с наклоном, не превышающим 30°. Каков тормозной путь этого автомобиля на горизонтальном участке такой же дороги при скорости 72 км/ч? [35 м] 16.36. Бассейн площадью 100 м2 заполнен водой до уровня 2 м и разделен пополам подвижной вертикальной перегородкой. Перегородку медленно передвинули так, что она разделила площадь бассейна в отношении 1:3. Какую работу А пришлось при этом совершить? Вода не проникала через перегородку и не переливалась через край бассейна. [650 кДж] 16.37. Автомобиль поднимается по склону со скоростью 60 км/ч. Спускаясь по тому же склону с выключенным мотором, он движется равномерно с той же скоростью. Какую мощность развивает двигатель на подъеме? Уклон равен 0,05. Масса автомобиля 2 т. [33 кВт] 16.38. Автомобиль движется вверх по пологому склону со скоростью 6 м/с и спускается по той же дороге со скоростью 9 м/с. С какой скоростью будет ехать этот автомобиль по горизонтальному участку этой же дороги? Мощность двигателя на всех трех участках одинакова. Сопротивлением воздуха можно пренебречь. [7,2 м/с] 16.39. Шлифовальный диск диаметра 30 см вращается с частотой 120 об/мин. Металлический брусок прижимают к цилиндрической поверхности диска с силой 100 Н. Коэффициент трения между бруском и диском 0,2. Какую мощность развивает двигатель, вращающий диск? [38 Вт] 16.40. На гладком горизонтальном столе лежит клин массы М и высоты h. Угол наклона поверхности клина к горизонту равен a. С клина соскальзывает без трения небольшое тело массы т. Какую скорость u приобретет тело в конце спуска? Найдите модуль и направление скорости. [ 16.41. Деревянный брусок висит на веревке длины l. В брусок выстрелили, пуля застряла в нем, и веревка отклонилась от вертикали на угол a. Какова скорость пули? Масса бруска М, масса пули т. Пуля летела горизонтально. [ 16.42. Человек прыгает в воду с высоты 10 м. На какую глубину он бы при этом погрузился, если бы можно было пренебречь силами сопротивления воздуха и воды? Масса человека 60 кг, объем его тела 66 л. [100 м] Статика.
17.1.Найти силы натяжения нитей АВ и ВС (рис. 1), если m = 1 кг, а a = 30°. 17.2.Найти равнодействующую сил (рис. 2): F1 = 50 Н; F2 = 100 Н; F3 = 60 Н; F4 = 200 Н; a = 30°, b = 60°. 17.3.Найти равнодействующую сил (рис. 3): F1 = 100 Н; F2 = 17.4.Определить силы в элементах АВ и ВС, если m = 120 кг, а a = 45°(рис. 4). 17.5.Определить силы в элементах АС и ВС, если АВ = 1,5 м; АС = 3 м; ВС = 4 м; m = 200 кг (рис. 5). 17.6.Грузы ml и m2 висят как показано на рис. 6. Зная углы a и b и массу m1, найти массу т2. 17.7.Грузы m1 и m2 висят на нити, перекинутой через неподвижный блок (рис. 7). В равновесии: a = 30°, b = 60°. Зная, что m2 = 2 кг, найти m1.
17.8.В закрытом пенале находятся карандаш и пружинка. Пенал ставят вертикально сначала так, что карандаш сверху, а затем переворачивают на 180° (рис. 8). При этом сила давления на нижний торец во втором случае в 1,2 раза больше, чем в первом. Найти силу давления в первом случае. Масса карандаша равна 10 г.
17.10.При взвешивании на неравноплечных весах, на одной чашке весов масса тела оказалась равна m1 = 3 кг, а на другой – m2 = 3,4 кг. Какова истинная масса тела? 17.11.Однородная балка массой М и длиной L подвешена на двух одинаковых веревках длиной L (2l > L). Веревки прикреплены к концам балки и подвешены к потолку в одной точке. С какой силой сжимается балка? 17.12.Однородная доска массой М одним концом упирается в стену и наклонена к полу под углом a. Какую минимальную силу необходимо приложить к ее противоположному концу, чтобы удержать ее в таком положении? 17.13.Однородный стержень АВ массой m подвешен горизонтально на двух вертикальных нитях. В точке С на расстоянии 1/4 длины стержня от конца А к стержню подвешен груз массой М (рис. 10). Определить силы натяжения нитей. 17.14.Какой максимальной длины мост можно построить из пяти плиточек домино способом, показанном на рис. 11. Длина одной плиточки равна l.
17.15.К верхней грани прямоугольного бруска прикладывают горизонтальную силу. Размеры бруска равны a ´ b,его масса равна m (рис. 12). При какой силе брусок опрокинется? При каком значении коэффициента трения это возможно? 17.16. Прямоугольный брусок со сторонами a и b кладут меньшим основанием на шероховатый стол. Упираясь острием карандаша в боковую грань, пытаются сдвинуть брусок с места (рис. 13). При этом заметили, что, если h < ho, то брусок сдвигается, а если h > ho, то брусок опрокидывается. Определить коэффициент трения бруска о стол. 17.17. Прямоугольный брусок со сторонами а и b лежит на плоской доске. Доску поднимают за один конец (рис. 14). При каком значении угла наклона доски брусок опрокинется? При каком значении коэффициента трения это возможно?
17.18. На неподвижной ленте транспортера, наклоненной под углом a к горизонту, лежит ящик размерами a ´ b (рис. 15). Лента трогается с места с очень большим ускорением. При каком значении коэффициента трения ящик опрокинется? Рассмотреть случаи движения ленты вверх и вниз. 17.19. Лестница стоит, опираясь на гладкую стену. Коэффициент трения лестницы о пол равен m. При каком минимальном значении угла наклона лестницы к полу она еще не скользит? 17.20. Однородный стержень АВ опирается о шероховатый пол и о гладкий выступ С. Угол наклона стержня к полу равен 45°, расстояние ВС = 0,25АВ (рис. 16). При каком коэффициенте трения возможно такое равновесия? 17.21. Легкая лестница стоит в углу, составляя с полом угол a = 60°. Коэффициент трения между лестницей и полом равен m = 0,4, а между лестницей и стеной трения нет. На какую высоту может по лестнице подняться человек, если длина лестницы равна l = 3 м? Массой лестницы пренебречь. 17.22. Лестница – стремянка состоит из двух одинаковых половинок, скрепленных вверху шарнирно. Масса каждой половинки равна М. Стремянку раскрывают на угол a и ставят на пол, а чтобы половинки не разъезжались внизу их связывают веревкой (рис. 17). Найти силу натяжения веревки. Трения нет. 17.23.На полу стоит лестница – стремянка. Одна часть у нее массивная, а другая невесомая (рис. 18). Нарисовать все силы, действующие на каждую часть стремянки.
17.24.Лестница – стремянка состоит из двух одинаковых по размерам половинок, соединенных вверху шарнирно. Массы половинок разные и равны m1 и m2. Половинки развели на угол 2a и поставили на гладкий пол, а чтобы половинки не разъезжались, их внизу связали веревкой. Найти силу натяжения веревки. 17.25.Лестница – стремянка состоит из двух половинок одинаковых по размерам, но разных по массе. Лестницу ставят на горизонтальный пол. На какой максимальный угол можно раздвинуть половинки, если коэффициент их трения о пол равен m = 0,5? Массы половинок равны 3m и m. 17.26.Однородный стержень одним концом упирается в вертикальную стену, а другой его конец удерживается с помощью нити, длина которой равна длине стержня (рис. 19). При каких значениях угла a стержень будет в равновесии, если коэффициент трения между ним и стеной равен m = 0,3? 17.27.Тонкий однородный стержень укреплен шарнирно в точке A и удерживается в равновесии горизонтальной нитью. Масса стержня равна m = 1 кг, угол a = 45° (рис. 20). Найти величину силы реакции в шарнире. 17.28.Шар массы М и радиуса R висит на нити длиной L у вертикальной стены (рис. 21). Найти силу натяжения нити и силу давления шара на стену. Трения нет.

17.29.Цилиндр массой М и радиусом R удерживается на наклонной плоскости намотанной на него нитью. Нить расположена горизонтально, угол наклона плоскости равен a (рис. 22). Найти силу натяжения нити. При каком значении коэффициента трения это возможно? 17.30.Балка удерживается в наклонном положении веревкой (рис. 23). Будет ли суммарная сила реакции, действующая на нижний конец балки, направлена вдоль нее? 17.31.Однородная доска массой М упирается в угол комнаты и удерживается под углом a к горизонту силой, приложенной к свободному концу доски и направленной перпендикулярно доске (рис. 24). С какой силой доска давит на стену? 17.32.От однородного стержня отрезали кусок длиной 40 см. На сколько сместился центр тяжести стержня? 17.33.Какой должна быть высота x треугольной части тонкой однородной пластины, чтобы центр тяжести пластины находился в точке O (рис. 25)? Длина прямоугольной части равна l. 17.34.Стержень спаян из двух одинаковых по сечению стержней, изготовленных из материалов с плотностями r и 2r (рис. 26). При каком отношении длин стержней l1/l2 центр тяжести системы будет находиться в плоскости спая? 17.35.Из однородного диска радиусом R вырезано круглое отверстие радиусом r, центр которого находится на расстоянии 1/2R от центра диска. На каком расстоянии от центра диска находится центр тяжести системы? 17.36.В вершинах квадрата со стороной a находятся точечные массы: m, 2m, 3m и 4m. С квадратом связана система координат (рис. 27). Найти координаты центра тяжести системы. 17.37.Квадрат со стороной a составлен из четырех тонких стержней одинакового сечения, сделанных из разных материалов с плотностями: r, 2r, 3r и 4r. С квадратом связана система координат (рис. 28). Найти координаты центра тяжести системы.
17.38.Квадратная рамка изготовлена из однородной проволоки. У нее отрезали одну сторону. Найти угол между средней стороной и вертикалью, если рамку подвесить на нити за: а) вершину A; б) вершину B (рис. 29).
17.39.Стержень длиной l, составленный из двух половинок, висит на двух нитях длиной l (рис. 30). Какой угол составляет стержень с горизонтом в равновесии, если половинки изготовлены из материалов с плотностями r и 2r?
17.40.Проволочный прямоугольный треугольник с углом a = 30° поставлен вертикально. По катетам треугольника без трения могут скользить две бусинки связанные нитью. Массы бусинок равны m1 = 100 г и m2 = 300 г. Определить силу натяжения нити и угол b в положении равновесия (рис. 31). Будет ли положение равновесия устойчивым? 17.41.Две гладкие наклонные плоскости наклонены под углами 30 и 60° к горизонту и составляют двугранный угол. В этот угол кладут гладкий однородный стержень (рис. 32). Какой угол будет составлять стержень с горизонтом в положении равновесия? Будет ли положение равновесия устойчивым? 17.42.Однородная балка массой М и длиной L удерживается горизонтально двумя роликовыми упорами и может двигаться в горизонтальном направлении (рис. 33). Найти минимальную и максимальную силу давления балки на нижний упор, если расстояние между упорами по горизонтали равно l. 17.43.Диск насажен на горизонтальный вал. Радиус диска равен R = 20 см, а радиус вала – r = 2 см. Для того, чтобы стащить диск с вала, его нужно тянуть с силой F = 100 Н. Для облегчения этой операции к ободу диска прикладывают касательную силу F1 = 8 Н и одновременно тянут его с силой F2. При каком значении F2 диск начнет сниматься с вала? 17.44.Невесомый стержень длиной l вращается с постоянной скоростью вокруг вертикальной оси O, проходящей через один из его концов. На другом конце стержня укреплен диск, который катится по горизонтальной поверхности (рис. 34). Масса диска т, коэффициент трения между диском и поверхностью и. Найти момент силы на оси O. Ось диска составляет угол a со стержнем.
17.47. В задаче № 11.46 высота ящика равна a, длина – h,а масса – m. Горизонтальную силу прикладывают сначала в точке A, а затем в точке B. При каком значении силы одна из опор оторвется от поверхности? 17.48.Автомобиль имеет две оси, расстояние между которыми равно l. Центр масс автомобиля расположен посередине между осями и на высоте h над землей. Какое максимальное ускорение может развить автомобиль, если ведущая ось: а) задняя; б) передняя? Коэффициент трения между колесами и дорогой равен m, размерами и массой колес пренебречь. 17.49.На гладкой горизонтальной поверхности лежит доска, прижатая однородным стержнем. Стержень наклонен к горизонту под углом а, а верхний конец его шарнирно закреплен (рис. 37). Для того, чтобы вытащить доску из под стержня, к ней надо приложить горизонтальную силу F1, направленную влево, или – F2, направленную вправо. Найти коэффициент трения между доской и стержнем. При каком значении коэффициента трения доску невозможно будет вытащить вправо? 17.50. Какой максимальной длины доску можно забить между двумя вертикальными стенами (рис. 38). Расстояние между стенами равно l, коэффициент трения между ними и доской равен m, массой доски пренебречь.
17.51.Ящик размерами a ´ b стоит с одной стороны на колесиках, а с другой – на жестком упоре. Ящик ставят на наклонную плоскость колесиками вниз (рис. 39). При этом он начинает скатываться, когда угол наклона плоскости равен a = 15°. При каком угле наклона начнет скатываться ящик, если его поставят на наклонную плоскость колесиками вверх? Принять b = a. Размерами колес и упоровпренебречь. 17.52.Кубик стоит наклонно в углу комнаты (рис. 40). При каком наименьшем значении угла a возможно такое равновесие, если коэффициент трения везде одинаков и равен m? 17.53.Два одинаковых однородных стержня соединены шарнирно и лежат на гладком горизонтальном цилиндре, радиус которого равен R (рис. 41). В положении равновесия угол между стержнями равен 90°. Какова длина стержней? Устойчиво ли такое положение равновесия?
17.54.Три одинаковых цилиндра сложены вместе и находятся между двумя вертикальными стенами, удерживаясь силами трения (рис. 42). Считая коэффициент трения везде одинаковым, найти при каком минимальном значении коэффициента трения возможно такое равновесие? 17.55. Три одинаковых цилиндра массой m каждый лежат, как показано на рис. 43. Поверхность и цилиндры гладкие. Чтобы цилиндры не разъехались, их связали веревкой. Найти силу натяжения веревки. Считать, что нижние цилиндры не давят друг на друга. 17.56. Невесомый обруч, к которому прикреплен небольшой грузик, стоит на доске, движущейся с горизонтальным ускорением a (рис. 44). Угол a известен и постоянен. Найти ускорение. Обруч по доске не скользит.
18.1.Жидкость в цилиндрическом сосуде сжимается поршнем. Сила, приложенная к поршню равна F, а площадь сечения сосуда S (рис. 1). Найти давление в жидкости. Атмосферным давлением, а также весом поршня и жидкости пренебречь. Изменится ли давление в жидкости, если нижняя часть поршня будет иметь более сложную форму? [ 18.2.Жидкость находиться между двумя поршнями площадью S1 и S2. На большой поршень действует сила F (рис. 2). Пренебрегая атмосферным давлением, найти давление в жидкости. [ 18.3.В U – образной трубке находится ртуть. На сколько повысится уровень ртути в одном колене, если в другое налить столб воды высотой H = 136 мм? [ 18.4.Три одинаковых вертикальных сосуда соединены в систему из трех сообщающихся сосудов. В систему залили ртуть. На сколько повысится уровень ртути в среднем сосуде, если в один из крайних налить слой воды высотой H1 = 102 мм, а в другой – слой воды высотой Н2 = 153 мм. [6,25 мм] 18.5. Два сообщающихся сосуда, площади сечения которых равны S1 и S2, закрыты невесомыми поршнями. Под поршнями находится жидкость с плотностью r. На сколько поднимется один из поршней, если на другой поставить гирьку массой m? [ 18.6. Концы U – образной трубки на l = 26 см выше уровня ртути. Какой максимальной высоты столб воды можно налить в одно из колен трубки? [ 18.7. На первом этаже здания давление воды в водопроводе равно 1 атм. На каком этаже вода из крана уже не течет, если высота каждого этажа равна 3 м? [на пятом] 18.8. В цилиндрический сосуд налили две несмешивающиеся жидкости в равных по массе количествах. Плотности жидкостей равны r1 = 1 г/см3 и r2 = 0,9 г/см3, а общая высота слоя жидкостей равна Н = 40 см. Найти давление жидкостей на дно сосуда. Атмосферное давление не учитывать. [ 18.9. Тело плавает в воде, погрузившись в нее на 3/4 своего объема. Найти плотность материала тела. [750 кг/м3] 18.10. Тело плавает в воде, погрузившись в нее на a = 0,75 своего объема. Какая часть объема тела будет погружена в спирт, плотность которого равна rсп = 0,8 г/см3? [ 18.11. Два тела: одно плотностью r1 = 1,5 г/см3 и объемом V1 = 0,5 см3; второе плотностью r2 = 0,5 г/см3 и объемом V2 = 1,5 см3 связали вместе и опустили в воду. Какая часть их общего объема будет погружена в воду? [ 18.12. Вес тела в жидкости с плотностью r1 равен P1, a в жидкости с плотностью r2 равен P2. Найти плотность тела. [ 18.13. Тело весом P, погруженное в жидкость с плотностью r1, весит P1, а погруженное в жидкость с неизвестной плотностью r2, весит Р2. Найти r2. [ 18.14.Тело плавает на границе двух несмешивающихся жидкостей с плотностями r1 и r2 (r1 < r2) При этом отношение объемов, погруженных в верхнюю и в нижнюю жидкости, равно V1/V2 = n. Определить плотность тела. [ 18.15.В цилиндрической банке высота уровня воды составляет ho = 15 см. Когда в нее опустили плавать пустую латунную чашку, уровень воды поднялся на Dh = 2,1 см. Какова будет высота уровня воды в банке, если чашку утопить? Плотность латуни равна rл = 8,4 г/см3. [ 18.16.Кусок сплава меди и серебра весит в воздухе P = 2,94 Н, а в воде – P1 = 2,65 Н. Сколько серебра и меди в куске? Плотности: меди – rм = 8,9 г/см3, серебра – rс = 10,5 г/см3. [ 18.17.Посередине большого озера просверлили прорубь. Толщина льда оказалась 8 м. Какой наименьшей длины веревку необходимо взять, чтобы зачерпнуть воду из проруби? [0,8 м] 18.18.На границе раздела двух несмешивающихся жидкостей с плотностями r1 и r2 плавает тело с плотностью r (r1 < r < r2). Какая часть объема тела находится в верхней жидкости? [ 18.19.Бревно длиной L = 3,5 м и поперечным сечением S = 0,04 м2 плавает в воде. Какую наибольшую массу может иметь человек, чтобы бревно не утонуло, когда человек встанет на него? Плотность дерева rд = 500 кг/м3. [ 18.20.Тело массой m, утонувшее в жидкости с плотностью r1, давит на дно с силой F. Какая часть тела будет погружена в жидкость с плотностью r2, на поверхности которой оно плавает? [ 18.21. Шар массой 1 кг наполовину погружен в воду и давит на дно с силой 8 Н. Найти плотность материала шара. [2500 кг/м3] 18.22. Шар плавает в воде, погрузившись в нее на 3/4 своего объема. Какая часть шара должна выступать из воды, чтобы сила его давления на дно равнялась половине силы тяжести шара? [0,625] 18.23. Льдина площадью 2 м2 плавает в воде. Когда на нее встал человек массой 70 кг высота верхнего края льдины над водой уменьшилась вдвое. Какова толщина льдины? [0,7 м] 18.24. Каким должен быть объем полости железного буя, для того чтобы он мог плавать на поверхности воды? Объем буя V, плотности железа и воды – rж и rв. [ 18.25. Для взятия пробы грунта на дно океана на стальном тросе опускается прибор. Найти предельную глубину погружения, если предел прочности стали на разрыв s= 4,8×10Н/м2. Плотность стали rст = 7800 кг/м3. Массой прибора пренебречь. [
18.29. В бак с жидкостью опущена длинная трубка диаметром d, к которой снизу плотно прилегает цилиндрический диск толщиной h и диаметром D (рис. 5). Плотность диска rд больше плотности жидкости rж. На какой глубине диск оторвется, если трубку медленно вытаскивать из жидкости? [ 18.30. Деревянный шарик, падая с высоты h1 = 60 см, погрузился в воду на глубину h2 = 60 см. На какую высоту выпрыгнет из воды этот шарик? Сопротивление воды считать постоянным, плотность дерева равна rд = 0,8 г/см3. [ 18.31. Два цилиндрических сообщающихся сосуда частично заполнены водой. В один из сосудов опускают тело массой m, которое плавает на поверхности. На сколько повысится уровень воды в сосудах? Площади сечения сосудов равны S1 и S2. [ 18.32. В цилиндрический сосуд массой M и площадью дна S налита вода до уровня h. Вода сверху закрыта поршнем, в котором имеется крючок. Каким будет давление под поршнем, если сосуд приподнять за этот крючок (рис. 6)? Атмосферное давление равно pa. [
18.34. Цилиндрический сосуд массой М и высотой h поставлен дном вверх на ровную горизонтальную резиновую поверхность. В дне сосуда имеется маленькое отверстие, в которое вставлена длинная тонкая трубка (рис. 7). Через трубку сосуд заполняется водой. До какой максимальной высоты можно в трубку налить воду? Площадь дна сосуда равна S. [
18.36. Легкий стержень свободно висит, касаясь нижним концом поверхности воды. Верхний конец стержня закреплен шарнирно (рис. 9). Вода начинает прибывать и ее уровень поднимается. Как зависит угол отклонения стержня от вертикали от высоты поднятия уровня воды? Длина стержня равна l, плотность стержня в n раз меньше плотности воды. Высота поднятия уровня воды отсчитывается от ее начального уровня. [ 18.37. Два цилиндрических сообщающихся сосуда соединены двумя трубками с кранами (рис. 10). Сначала краны открыты и в сосуды наливают жидкость. Затем краны закрывают и жидкость в сосуде 2 нагревают, в результате чего уровень жидкости в этом сосуде слегка повысился. Куда потечет жидкость, если открыть: а) кран K1; б) кран К2; в) оба крана? [а) Никуда; б) из 2 в 1; в) возникает циркуляция: внизу из 1 в 2, вверху из 2 в 1]
18.38. Два расширяющихся кверху сосуда соединены трубкой с краном и заполнены жидкостью (рис. 11). Сначала кран открыт. Затем его закрывают и жидкость в сосуде 2 нагревают, в результате чего уровень жидкости в нем слегка повысился. Куда потечет жидкость, если кран открыть? [из 1 в 2] 18.39.Два одинаковых по размеру шарика массами m1 и m2 (m1 < m2) связаны нитью и тонут в воде с постоянной скоростью. Определить силу натяжения нити. [ 18.40.Однородная палочка, шарнирно прикрепленная к стенке бассейна, высовывается из воды на 0,1 своей длины (рис. 12). Найти плотность материала палочки. [810 кг/м3]
18.42.В цилиндрический сосуд с площадью дна S налита жидкость плотностью r. Сверху непосредственно на жидкости лежит массивный поршень с пробкой (рис. 13). Поршень и пробка сделаны из одного материала, имеют одинаковую толщину h и могут двигаться без зазора и без трения. Какую работу надо совершить, чтобы вытащить пробку? Площадь пробки равна S1. [ где m1 и m2 – масса поршня и пробки; h1 – высота на которую опустился поршень при вытаскивании пробки. Дополнительные соотношения:
18.44.Однородная деревянная рейка массой m и длиной l плавает в воде между двумя вертикальными стенками (рис. 14). Расстояние между стенками d < l, а отношение плотностей рейки и воды равно a < 1. С какой силой рейка давит на стенки? Трения нет. [
18.46.Внутри вертикального узкого стакана стоит вертикальная пружина, длина которой равна высоте стакана. Если в стакан поставить однородный стержень, длина которого тоже равна высоте стакана, то четвертая часть его будет высовываться из стакана (рис. 16). Если в стакан доверху налить воду, то из стакана будет высовываться половина стержня. Найти плотность материала стержня. [ 18.47.Однородный стержень плотностью r плавает на границе раздела двух несмешивающихся жидкостей с плотностями r1 и r2 (r1 < r < r2). При каком соотношении между плотностями устойчивым положением стержня будет вертикальное? [Вертикальное положение не может быть устойчивым] 18.48.В воде плавает доска массой М. Плотность доски вдвое меньше плотности воды. Когда на конец доски села лягушка, верхний край доски с этого конца опустился как раз до уровня воды. Найти массу лягушки. [ 18.49.Воздушный шар опускается с постоянной скоростью. Когда из него выбросили груз массой m, он начал подниматься с той же постоянной скоростью. Найти силу сопротивления воздуха при этой скорости. [
18.51.В вертикальном цилиндрическом сосуде, доверху заполненном водой и закрытом крышкой, на нитях висят два шарика: сверху стальной; снизу пробковый (рис. 17). Как будут вести себя шарики, если сосуд начнут медленно раскручивать вокруг его оси? [верхний шарик будет отклоняться от оси, а нижний – к оси]
18.53.Большая плоская льдина плавает в воде. В льдине просверлили прорубь площадью S = 300 см2. Вода в проруби оказалась на глубине h = 10 см. Какое максимальное количество масла можно налить в прорубь? Плотность масла равна rм = 800 кг/м3. [ 18.54.Два шарика, сделанные из одного материала, имеют объемы: V и 3V. Шарики связали невесомой нитью, перекинутой через неподвижный блок, и отпустили над поверхностью воды. Когда один из шариков погрузился в воду ускорение системы изменилось на противоположное. Найти плотность материала шариков. Сопротивление воды и трение не учитывать. [ 18.55.Тело массой m тонет в воде с ускорением a. С какой силой его надо тянуть вверх, чтобы оно поднималось с тем же ускорением? Сопротивление не учитывать. [
18.57.Цилиндрический сосуд радиусом R, заполненный жидкостью с плотностью r, вращается вокруг своей вертикальной оси с угловой скоростью w. В сосуде находится маленький шарик радиусом r и плотностью 2r (r << R). С какой силой шарик давит на боковую поверхность сосуда? [ 18.58.Аквариум с водой на колесиках скатывается с наклонной плоскости без трения. Как располагается уровень поверхности воды при установившемся скатывании? [Параллельно наклонной плоскости]
Давление в жидкости.
 19.1. В жидкости находится прямоугольная призма, размеры которой показаны на рисунке. Найдите сумму сил, действующих на переднюю и нижнюю грань призмы, если давление жидкости 2×105 Па. Чему равна сумма сил, действующих на призму? [ 19.1. В жидкости находится прямоугольная призма, размеры которой показаны на рисунке. Найдите сумму сил, действующих на переднюю и нижнюю грань призмы, если давление жидкости 2×105 Па. Чему равна сумма сил, действующих на призму? [  H. Нуль] H. Нуль] 19.2. Результирующая сила, действующая со стороны сжатой жидкости на три грани правильного тетраэдра, равна F. Длина ребра тетраэдра а. Определите давление жидкости. [
19.4. Шар перекрывает отверстие радиуса r в плоской стенке, разделяющей жидкости с давлениями 3P и Р. С какой силой прижимается шар к отверстию? [ 19.5. Коническая пробка перекрывает сразу два отверстия в плоском сосуде, заполненном жидкостью при давлении Р. Радиусы отверстий r и R. Определите силу, действующую на пробку со стороны жидкости. [ 19.6*. Сферический баллон радиуса R со стенками толщины D << R разрывается внутренним давлением Р. Определите предел прочности материала стенок. [ < |



 ]
] ]
] 16.3. Легкая пружина жесткости k и длины L стоит вертикально на столе и не прикреплена к нему. На пружину падает небольшой шарик массой m, имеющий начальную скорость равную нулю. Пружина упруго деформируется, и шарик подскакивает вертикально вверх (рис. 16.1). Максимальная скорость шарика при его движении оказалась равной vmax. На какую высоту поднимется центр тяжести пружины?
16.3. Легкая пружина жесткости k и длины L стоит вертикально на столе и не прикреплена к нему. На пружину падает небольшой шарик массой m, имеющий начальную скорость равную нулю. Пружина упруго деформируется, и шарик подскакивает вертикально вверх (рис. 16.1). Максимальная скорость шарика при его движении оказалась равной vmax. На какую высоту поднимется центр тяжести пружины? ]
] ]
] ]
]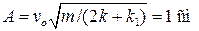 ]
] ]
] 16.8. На гладком столе покоится брусок массой M = 20 г, прикрепленный пружиной жесткости k = 50 Н/м к стене. В брусок ударяется шарик массой m = 10 г, движущийся по столу со скоростью vo = 30 м/с, направленной вдоль пружины. Считая соударение шарика и бруска упругим, найти амплитуду A колебаний бруска после удара. [
16.8. На гладком столе покоится брусок массой M = 20 г, прикрепленный пружиной жесткости k = 50 Н/м к стене. В брусок ударяется шарик массой m = 10 г, движущийся по столу со скоростью vo = 30 м/с, направленной вдоль пружины. Считая соударение шарика и бруска упругим, найти амплитуду A колебаний бруска после удара. [  ]
] ]
] ]
] ]
] ]
] ]
] ]
] ]
]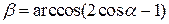 ]
] ]
] ]
]



 Н; F3 = 50 Н; a = 60°; b = 30°.
Н; F3 = 50 Н; a = 60°; b = 30°.



 17.9.Однородная балка лежит на платформе, свешиваясь с нее на 0,25 своей длины (рис. 9). Когда конец B балки потянули вниз с силой F = 300 Н, противоположный конец начал отрываться от платформы. Чему равен вес балки?
17.9.Однородная балка лежит на платформе, свешиваясь с нее на 0,25 своей длины (рис. 9). Когда конец B балки потянули вниз с силой F = 300 Н, противоположный конец начал отрываться от платформы. Чему равен вес балки?






















 17.45.Тележка приводится в движение пружиной как показано на рис. 35. В начальном состоянии тележка удерживается нитью, а пружина растянута силой F. Точка крепления пружины к колесу находится на расстоянии l над центром колеса. Радиус колеса тележки равен R, а масса тележки – m. С каким ускорением начнет двигаться тележка, если перерезать нить? Массой колес пренебречь. Считать, что колеса не проскальзывают.
17.45.Тележка приводится в движение пружиной как показано на рис. 35. В начальном состоянии тележка удерживается нитью, а пружина растянута силой F. Точка крепления пружины к колесу находится на расстоянии l над центром колеса. Радиус колеса тележки равен R, а масса тележки – m. С каким ускорением начнет двигаться тележка, если перерезать нить? Массой колес пренебречь. Считать, что колеса не проскальзывают. 17.46.Однородный прямоугольный ящик лежит на гладкой горизонтальной поверхности на двух опорах. Ящик начинают тянуть горизонтальной силой, приложенной в точке A (рис. 36). Какая из опор при этом сильнее давит на поверхность? А если сила приложена в точке B?
17.46.Однородный прямоугольный ящик лежит на гладкой горизонтальной поверхности на двух опорах. Ящик начинают тянуть горизонтальной силой, приложенной в точке A (рис. 36). Какая из опор при этом сильнее давит на поверхность? А если сила приложена в точке B?







 Гидростатика.
Гидростатика. ; не изменится]
; не изменится] ]
] мм]
мм] ]
] см]
см] Па]
Па] ]
] ]
]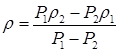 ]
] ]
] ]
] см]
см] кг;
кг; 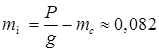 кг]
кг] ]
] кг]
кг] ]
] ]
] км]
км] 18.26. В цилиндрическом стакане с водой плавает льдинка, привязанная нитью ко дну (рис. 3). Когда льдинка растаяла уровень воды понизился на Dh. Каково было начальное натяжение нити? Площадь дна стакана равна S. [
18.26. В цилиндрическом стакане с водой плавает льдинка, привязанная нитью ко дну (рис. 3). Когда льдинка растаяла уровень воды понизился на Dh. Каково было начальное натяжение нити? Площадь дна стакана равна S. [  ]
] 18.27. На чашках погруженных в воду равноплечных весов находятся алюминиевый и железный шары одинаковой массы m. Определить массу сплошного шара из меди, который необходимо добавить для восстановления равновесия. Плотности алюминия, железа и меди: rа, rж и rм. [
18.27. На чашках погруженных в воду равноплечных весов находятся алюминиевый и железный шары одинаковой массы m. Определить массу сплошного шара из меди, который необходимо добавить для восстановления равновесия. Плотности алюминия, железа и меди: rа, rж и rм. [  ]
] 18.28. К концу однородной палочки массой m = 4 г подвешен на нити шар радиусом r = 0,5 см. Палочка лежит на краю стакана (рис 4). В равновесии шар погружен в воду ровно наполовину. В каком отношении делится палочка точкой опоры? Плотность шара r = 2,7 г/см3. [
18.28. К концу однородной палочки массой m = 4 г подвешен на нити шар радиусом r = 0,5 см. Палочка лежит на краю стакана (рис 4). В равновесии шар погружен в воду ровно наполовину. В каком отношении делится палочка точкой опоры? Плотность шара r = 2,7 г/см3. [  ]
] ]
] см]
см] ]
] ]
]
 18.33. Первый шарик всплывает в воде с постоянной установившейся скоростью vo. Второй такой же по размеру шарик тонет в воде с постоянной установившейся скоростью 2vo. С какой постоянной установившейся скоростью будут тонуть эти шарики, если связать их нитью? Считать, что сила сопротивления пропорциональна скорости. [
18.33. Первый шарик всплывает в воде с постоянной установившейся скоростью vo. Второй такой же по размеру шарик тонет в воде с постоянной установившейся скоростью 2vo. С какой постоянной установившейся скоростью будут тонуть эти шарики, если связать их нитью? Считать, что сила сопротивления пропорциональна скорости. [  ; при установившемся движении сила тяжести, сила Архимеда и сила сопротивления уравновешивают друг друга]
; при установившемся движении сила тяжести, сила Архимеда и сила сопротивления уравновешивают друг друга] ; вода начнет приподнимать сосуд и вытекать из-под него, когда сила давления воды снизу вверх на дно сосуда
; вода начнет приподнимать сосуд и вытекать из-под него, когда сила давления воды снизу вверх на дно сосуда  станет равна силе тяжести сосуда Mg]
станет равна силе тяжести сосуда Mg]
 18.35. Полая тонкая полусфера массой М и радиусом R лежит на ровной горизонтальной резиновой поверхности. В верхней части полусферы имеется маленькое отверстие, в которое вставлена длинная тонкая трубка (рис. 8). Через трубку полусфера заполняется водой. До какой максимальной высоты можно налить в трубку воду? [
18.35. Полая тонкая полусфера массой М и радиусом R лежит на ровной горизонтальной резиновой поверхности. В верхней части полусферы имеется маленькое отверстие, в которое вставлена длинная тонкая трубка (рис. 8). Через трубку полусфера заполняется водой. До какой максимальной высоты можно налить в трубку воду? [  ; Сила, с которой полусфера и вода давят на поверхность, равна:
; Сила, с которой полусфера и вода давят на поверхность, равна:  , где N – сила давления полусферы;
, где N – сила давления полусферы;  . С другой стороны, эта сила равна суммарной силе тяжести системы:
. С другой стороны, эта сила равна суммарной силе тяжести системы:  – где V – объем полусферы (массу воды в трубке не учитываем). Когда вода начнет приподнимать полусферу и вытекать из-под нее, сила давления полусферы на поверхность станет равна нулю.]
– где V – объем полусферы (массу воды в трубке не учитываем). Когда вода начнет приподнимать полусферу и вытекать из-под нее, сила давления полусферы на поверхность станет равна нулю.] ]
]


 ]
] 18.41.Какую работу необходимо совершить, чтобы утопить плоскую льдину массой M = 1000 кг и площадью S = 2 м2? [
18.41.Какую работу необходимо совершить, чтобы утопить плоскую льдину массой M = 1000 кг и площадью S = 2 м2? [  Дж]
Дж] ; работа равна разности потенциальных энергий системы в конечном и начальном состояниях. Если за ноль потенциальной энергии взять нижнюю грань поршня в конечном состоянии, то начальная и конечная энергии системы равны:
; работа равна разности потенциальных энергий системы в конечном и начальном состояниях. Если за ноль потенциальной энергии взять нижнюю грань поршня в конечном состоянии, то начальная и конечная энергии системы равны:  и
и 
 .]
.] 13.43.До какой высоты надо налить воду в цилиндрический сосуд радиусом R, чтобы силы давления воды на дно и на боковую поверхность были равны? [h = R]
13.43.До какой высоты надо налить воду в цилиндрический сосуд радиусом R, чтобы силы давления воды на дно и на боковую поверхность были равны? [h = R] ]
]
 18.45.Кубик, сделанный из материала, плотность которого вдвое меньше плотности воды, плавает в воде. Какое из двух показанных положений кубика будет устойчивым (рис. 15)? [Первое; устойчивым будет положение, в котором потенциальная энергия системы меньше. Так как энергия кубика в обоих положениях одинакова, то меньшей энергией будет обладать то положение, в котором потенциальная энергии воды меньше. Но потенциальная энергия воды равна ее энергии без погруженного кубика минус энергия воды в объеме погруженной части кубика. Значит устойчивым будет положение в котором центр масс погруженной части кубика выше. Центр масс однородного треугольника находится в точке пересечения медиан.]
18.45.Кубик, сделанный из материала, плотность которого вдвое меньше плотности воды, плавает в воде. Какое из двух показанных положений кубика будет устойчивым (рис. 15)? [Первое; устойчивым будет положение, в котором потенциальная энергия системы меньше. Так как энергия кубика в обоих положениях одинакова, то меньшей энергией будет обладать то положение, в котором потенциальная энергии воды меньше. Но потенциальная энергия воды равна ее энергии без погруженного кубика минус энергия воды в объеме погруженной части кубика. Значит устойчивым будет положение в котором центр масс погруженной части кубика выше. Центр масс однородного треугольника находится в точке пересечения медиан.] кг/м3]
кг/м3] ]
] ]
] 18.50.Воздушный шар опускается с постоянной скоростью. Общая масса оболочки и груза равна М, объем оболочки – V, плотность воздуха – rв, плотность газа в оболочке – r. Какой массы груз надо выбросить, чтобы шар начал подниматься с той же постоянной скоростью? Считать, что сила сопротивления пропорциональна скорости. [
18.50.Воздушный шар опускается с постоянной скоростью. Общая масса оболочки и груза равна М, объем оболочки – V, плотность воздуха – rв, плотность газа в оболочке – r. Какой массы груз надо выбросить, чтобы шар начал подниматься с той же постоянной скоростью? Считать, что сила сопротивления пропорциональна скорости. [  ]
] 18.52.Три одинаковых бревна плавают в воде между вертикальными стенками канала. Расстояние между стенками слегка больше удвоенного диаметра бревен, а верхние бревна погружены в воду ровно наполовину (рис. 18). С какой силой бревна давят на стенки канала, если масса каждого бревна равна m? Трения нет. [
18.52.Три одинаковых бревна плавают в воде между вертикальными стенками канала. Расстояние между стенками слегка больше удвоенного диаметра бревен, а верхние бревна погружены в воду ровно наполовину (рис. 18). С какой силой бревна давят на стенки канала, если масса каждого бревна равна m? Трения нет. [  ]
]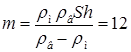 кг]
кг] кг/м3]
кг/м3] ]
] 18.56.Тонкий однородный стержень длиной l = 1 м, сделанный из материала с плотностью r = 0,91 г/см3, шарнирно прикреплен к стенке бассейна и опирается на дно так, что составляет угол a = 60° с вертикалью (рис. 19). В бассейн начинают наливать воду. При какой высоте уровня воды стержень перестанет давить на дно? [
18.56.Тонкий однородный стержень длиной l = 1 м, сделанный из материала с плотностью r = 0,91 г/см3, шарнирно прикреплен к стенке бассейна и опирается на дно так, что составляет угол a = 60° с вертикалью (рис. 19). В бассейн начинают наливать воду. При какой высоте уровня воды стержень перестанет давить на дно? [  м]
м] ]
]

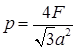 ]
] 19.3. В трубе находится поршень, продольное сечение которого показано на рисунке. Давление жидкости с обеих сторон поршня одинаково. Находится ли поршень в равновесии? [Да]
19.3. В трубе находится поршень, продольное сечение которого показано на рисунке. Давление жидкости с обеих сторон поршня одинаково. Находится ли поршень в равновесии? [Да] ]
] ]
]