 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Импульс. Закон сохранения импульса.
Мінестерство освіти і науки, молоді та спорту украіни Запорізький авіаційний коледж ім. О. Г. Івченка
Домашня самостійна робота Механіка Для студентів ІІ курсу з дисципліни «Фізика*» Розробив викладач ____________ (Гуляєва Т.В.) Розглянуто та затверджено На засіданні ПЦК _фізико-математичних дисциплін_ Протокол № ____ від _______________ 2013 Голова ПЦК ___________ (Костенко Л. І.)
Запоріжжя Зміст
Основні формули та закони ………………………………………………… 4 Задачі для самостійного розв’язання ………………………………………. 13 Задачі для самостійного розв’язання за окремими темами ………………. 15 Импульс. Закон сохранения импульса …………………………………. 16 Работа. Мощность. Энергия …………………………………………….. 21 Закон сохранения механической энергии и импульса ….………….….. 26 Прямой центральный абсолютно упругий удар …………………….…. 30 Непрямой упругий удар ……………………………………………….… 31 Неупругий удар …………………………………………………………... 31 Комплексные задачи на энергию и импульс …………………………… 32 Статика ………………………………………………………………….… 38 Гидростатика …………………………………………………………...… 44 Давление в жидкости………………….………………………………….. 52 Плавание. Закон Архимеда ……………………………………………… 56 Движение идеальной жидкости ………………………………………… 59 Течение вязкой жидкости ……………………………………………….. 63 Механика твердого тела. Момент импульса …………………………… 63
Відповіді ………………………………………………………………….. 67 Література ………………………………………………………………… 73
Основні формули та закони
Задачі для самостійного розв’язання
Задача 1. За відомим рівнянням руху, де х0, V0, a, δ, ω подано в системі СІ 1. Записати рівняння залежності швидкості та прискорення від часу. 2. Знайти модуль швидкості та прискорення через 2 с та 5 с після початку руху. 3. Знайти модуль переміщення матеріальної точки від початку 2с до кінця 5 с. 4. Записати рівняння залежності рівнодійної сили, що діє на матеріальну точку та її модуль через 3 с після початку руху, якщо маса матеріальної точки т. 5. Знайти імпульс матеріальної точки через 1 с та 2 с від початку руху та зміну імпульсу за цей час. 6. Знайти кінетичну, потенціальну та повну енергію матеріальної точки через 1 с та 2 с від початку руху.
Задача 2. Диск обертається навколо нерухомої осі так, що залежність кута повороту диску від часу задається наступним рівнянням: 1. Кутову швидкість та кутове прискорення. 2. Нормальне, тангенціальне та повне прискорення для матеріальної точки, що знаходиться на відстані R від осі. 3. Кут повороту, при якому повне прискорення складає кут α з радіусом диска.
Задача 3. Система зв’язаних тіл масою m1, m2, m3 знаходиться на похилій площині. Кути α і β – кути нахилу похилої площини до горизонту. Коефіцієнт тертя між тілами і поверхнею μ. Тіла рухається з прискоренням а. Знайти прискорення та сили натягу нитки між тілами. Розглянути два випадки: 1) блок невагомий; 2) блок має масу М та радіус R.
Задачі для самостійного розв’язання за окремими темами
Наступні задачі розв’язати виходячи з номером за списком.
Импульс. Закон сохранения импульса. 10.1. Материальная точка массой m с постоянной угловой скоростью w по окружности радиусом R. Определить изменение импульса за 1/4 периода. [
10.3. К телу массой m, движущемуся прямолинейно по гладкой горизонтальной поверхности, приложена по направлению его движения сила, изменяющаяся по линейному закону (рис. 10.1). Определить конечную скорость тела, если начальная скорость vo. Значение параметров конечного времени t и конечной силы Fo считать известными. [ 10.4. Автомобиль массой m = 2×103 кг движется со скоростью v = 90 км/ч. В момент времени t = 0 на него начинает действовать тормозящая сила F, которая нарастает по линейному закону. Через какое время автомобиль остановится? [ 10.5. Тело массой 1 кг брошено под углом к углом к горизонту. За время полета его импульс изменился на p = 10 кг×м/с. Определить наибольшую высоту подъема тела. [ 10.6. Металлический шарик, падая с высоты h1 = 1 м на стальную плиту, отскакивая на высоту h2 = 0,81 м. Во сколько раз уменьшается импульс шарика при ударе? [в 0,9 раз] 10.7. Какова средняя сила давления F на плечо при стрельбе из автомата, если масса пули m = 10 г, а скорость пули при вылете из канала ствола v = 300 м/с? автомат делает 300 выстрелов в минуту. [15 H; 60 c] 10.8. Для проведения огневых испытаний жидкостный ракетный двигатель закрепили на стенде. С какой силой он действует на стенд, если скорость истечения продуктов сгорания из сопла v, а расход топлива за t секунд составил m кг? [F = mv/t] 10.9. Платформой массой M начинает двигаться вправо под действием постоянной силы F. Из неподвижного бункера на нее высыпается песок. Скорость погрузки постоянна и равна m кг/с. Пренебрегая трением, найти зависимость от времени ускорения a платформы в процессе погрузки. Определить ускорение a1 платформы в случае, если песок не насыпается на платформу, а из наполненной высыпается через отверстие в ее дне с постоянной скоростью m кг/с. [ 10.10. Тело массой m, имеющее начальную скорость vo, попадает в вязкую среду, сила сопротивления движению тела которой пропорциональна его скорости: F = av, где a – известный коэффициент. Определите путь, пройденный телом до остановки. [S = mvo/a] 10.11. Водометный катер движется с постоянной скоростью, забирая забортную воду и выбрасывая назад струю со скоростью u = 20 м/с относительно катера. Площадь поперечного сечения струи S = 0,01 м2. Найдите скорость катера, если действующая на него сила сопротивления пропорциональна квадрату скорости: F = kv2, причем k = 7,5 Нс2/м2. [13,4 м/с] 10.12. Один конец каната удерживают на высоте h от земли, второй его конец касается земли. В момент времени t = 0 канат отпускают и он начинает свободно падать на землю. Получите аналитическую зависимость силы, с которой канат будет давить на землю, от времени. Масса единицы длины каната равна r. [ 10.13. Два шарика, изготовленных из одного и того же материала, падают в облаке пыли. Во сколько раз отличаются установившиеся скорости падения шариков, если диаметр одного из них вдвое больше диаметра другого? Пыль не прилипает к шарикам, и масса их в процессе движения не изменяется. [скорость большего шарика в 10.14. На поверхности воды находится в покое лодка. Человек, находящийся в ней, переходит с кормы на нос. Как будет двигаться лодка, если сила сопротивления движению пропорциональна скорости лодки? [лодка вернется в ту же точку, в которой она находилась до начала движения] 10.15. Металлический шарик массой m падает на металлическую горизонтальную поверхность. В момент столкновения скорость шарика равна v и направлена под углом a к нормали. Столкновение абсолютно упругое. Определить изменение импульса шарика, если: а) поверхность неподвижна; б) поверхность движется со скоростью u навстречу шарику вдоль нормали. [a) 10.16. Шарик массой m падает с высоты h на горизонтальную поверхность. Приняв длительность удара равной t, определить среднюю силу удара в случаях: а) удар абсолютно упругий; б) удар абсолютно неупругий; в) удар абсолютно упругий, а поверхность наклонена под углом a к горизонту. [a) 10.17. Тело массой m брошено под углом a к горизонту с начальной скоростью vo. Найти изменение импульса тела за время полета. [ 10.18. Под каким углом к горизонту необходимо бросить камень, чтобы модуль изменения импульса за все время полета был равен модулю начального импульса? [a = 30o] 10.19. Шарик массой m падает с высоты h на неподвижную горизонтальную плиту. Считая столкновения шарика с плитой абсолютно упругими, определить среднюю силу давления шарика на плиту. [<F> = mg] 10.20. С высоты h на горизонтальную поверхность сыпется песок. За одну секунду высыпается масса песка равная m. Найти зависимость силы давления песка на поверхность от времени. [ 10.21. Тонкая стальная цепочка висит вертикально, касаясь нижним концом стола. Масса цепочки равна m, длина l. В момент t = 0 цепочку отпускают. Найти зависимость силы давления цепочки на стол от времени. [ 10.22. Тонкая цепочка перекинута через неподвижный блок. Причем часть ее лежит на столе высотой h, а часть – на полу. Цепочку отпускают. Найти установившуюся скорость движения цепочки. Блок идеальный. [ 10.23. Ракета с площадью поперечного сечения S, двигаясь в космическом пространстве со скоростью u, попадает в неподвижное облако космической пыли со средней плотностью r. Какую силу тяги должны развивать двигатели ракеты, чтобы ее скорость осталась прежней? Столкновения пылинок с ракетой считать неупругими, изменением массы ракеты пренебречь. [ 10.24. Ракета массой M неподвижно зависла над поверхностью земли. Сколько топлива в единицу времени сжигает ракета, если скорость истечения продуктов сгорания из ракеты равна u? Как изменится результат, если ракета начнет подниматься с ускорением a? [ 10.25. Тело массой m вращается с постоянной скоростью v по окружности радиусом R. Определить модуль среднего значения центростремительной силы за: а) четверть периода; б) полпериода; в) период. [a) 10.26. Тележка массой M едет без трения со скоростью uo. На нее с высоты h без начальной скорости падает тело массой m. В результате столкновения вертикальная составляющая скорости тела по величине не изменяется. Определить полную скорость, с которой тело отскочит от тележки и скорость тележки после столкновения. Коэффициент трения между телом и тележкой равен m, длительность удара очень мала. [
10.27. На весах стоит бункер с песком общей массой M. Заслонку бункера открывают и песок начинает высыпаться из бункера на весы. Что будут показывать весы, если песок высыпается с высоты H и в секунду высыпается m кг песка? [Mg]
10.29. Однородный массивный диск лежит на гладкой горизонтальной поверхности (рис. 10.2). На диск в точках A и B начинают действовать горизонтальные, одинаковые по модулю и противоположно направленные силы. Как будет двигаться диск? [вращаться вокруг центра диска по часовой стрелке]
10.31. На гладкой горизонтальной поверхности лежит обруч, на котором сидит жук. Как будут двигаться жук и обруч, если жук поползет по обручу? 10.32. Ракета летит с работающим двигателем. Причем скорость ракеты больше скорости вылета реактивной струи из ракеты. Увеличивается ли при этом скорость ракеты? [увеличивается] 10.33. По изогнутой под прямым углом трубе течет вода. Действует ли вода на трубу и, если да, то в каком направлении? Какова эта сила, если скорость течения воды равна v, площадь сечения трубы равна S, а плотность воды – r? Вязкости нет. [сила действует в месте изгиба в направлении биссектрисы угла и равна 10.34. На веревке, перекинутой через неподвижный блок, висят две обезьяны одинаковой массы и на одинаковом расстоянии от блока. Обезьяны начинают одновременно подниматься вверх. Скорость одной обезьяны равна v, a второй – 2v. Какая обезьяна достигнет блока раньше? [одновременно] 10.35. По гладкой наклонной плоскости с углом наклона a скатывается мешок с мукой и попадает на горизонтальный пол. На каком расстоянии от наклонной плоскости остановится мешок, если он скатывается с высоты H, а коэффициент трения мешка о пол равен m? [ 10.36. На тело, движущееся со скоростью vo, начинает действовать постоянная сила. Спустя время t скорость тела становится перпендикулярна начальной, не изменившись по модулю. Какой станет скорость тела спустя еще t? [ 10.37. Лодку оттолкнули от берега со скоростью vo. Какое расстояние проплывет лодка до остановки, если масса лодки равна m, а сила сопротивления пропорциональна скорости и равна kv? [
10.39. На нити висит тело массой m необтекаемой формы. На какой угол от вертикали отклонится нить, если дует горизонтальный ветер со скоростью v? Площадь вертикального сечения стержня равна S, плотность воздуха r. [ 10.40. Брусок массой m = 1 кг лежит на горизонтальной поверхности. Коэффициент трения между бруском и поверхностью равен m = 0,1. На боковую грань бруска направляется горизонтальная струя воды со скоростью v = 10 м/с. Площадь сечения струи S = 2 см2. С какой скоростью движется брусок? [ 10.41. Пуля массой m попадает в неподвижный брусок, покоящийся на гладкой горизонтальной поверхности. Масса бруска M, скорость пули vo направлена горизонтально. Пуля застревает в бруске. Определить скорость движения бруска после попадания в него пули. [ 10.42. Пуля массой m,летящая горизонтально со скоростью vo попадает в брусок, лежащий на гладком полу, и пробивает его насквозь. Масса бруска M, скорость пули после вылета v. Определить скорость движения бруска. [ 10.43. На тележку массой M, движущуюся со скоростью v, сверху падает груз массой m. Определить скорость тележки u после падения груза. [ 10.44. Конькобежец массой M,стоящий на льду, бросает под углом a к горизонту камень массой m. Определить скорость конькобежца после броска, если скорость камня vo. [ 10.45. На гладкой горизонтальной плоскости стоит брусок массой M. К бруску привязана нить длиной L,на конце которой закреплен шарик массой m. В начальный момент нить была отклонена на некоторый угол и отпущена без начальной скорости. Найдите скорость бруска в момент, когда нить проходит через вертикальное положение, зная, что ее угловая скорость в этот момент равна w. [ 10.46. Снаряд, который летел в горизонтальном направлении со скоростью v,разрывается на два осколка массой m1 и m2.Скорость осколка массой m1 равна v1, и направлена вертикально вверх. Определить модуль и направление скорости осколка массой m2. [ 10.47. Струя сечением 6 см2 ударяет из брандспойта в стенку под углом 60° к нормали и под тем же углом упруго отражается от нее. Скорость струи 15 м/с. С какой силой F струя давит на стену? [135 H] 10.48. Ракета влетает в пылевое облако со скоростью v относительно облака. Пылинки оказались липкими: они соударялись с ракетой неупруго. Чтобы скорость движения не изменялась, пришлось включить двигатель, развивающий силу тяги F. Какая была бы нужна сила тяги для сохранения скорости, если бы: а) ракета влетела в то же облако со скоростью 2v, б) влетела со скоростью v в другое облако, где концентрация частиц (т.е. число частиц в единице объема) в три раза больше? [4F; 3F] 10.49. На гладком льду лежит цилиндрическое однородное бревно длиной l. Один из его концов стали медленно поднимать с помощью веревки. Когда угол между бревном и поверхностью льда стал равным a, вертикально натянутая веревка оборвалась. На какое расстояние сместится при падении бревна его нижний конец? [ 10.50. На сколько сместится неподвижная лодка массой 280 кг, если человек массой 70 кг перейдет с ее носа на корму? Расстояние от носа до кормы 5 м, сопротивление воды пренебрежимо мало. [1 м] 10.52. Два рыбака ловят рыбу в озере, сидя в неподвижной лодке. Куда и на сколько сместится лодка, если рыбаки поменяются местами? Масса лодки 280 кг, масса одного рыбака 70 кг, масса второго — 140 кг, расстояние между рыбаками 5 м. Сопротивлением воды можно пренебречь. [0,71 м] 10.53. Пушка массой 800 кг выстреливает ядро массой 10 кг с начальной скоростью 200 м/с относительно Земли под углом 60° к горизонту. Какова скорость отката пушки? Трением можно пренебречь. [1,25 м/с] 10.54. На гладком столе находится обруч массы М и радиуса R. По обручу ползет жук массы т. По каким траекториям движутся жук и центр обруча? [по окружностям с радиусами 10.55.По длинному склону, образующему угол a с горизонтом, съезжает тележка, на которой установлен бак с водой. Через отверстие площадью S в задней стенке бака вытекает струя воды со скоростью v относительно бака. Поверхность воды в баке установилась параллельно склону. Найдите коэффициент сопротивления движению m. Масса тележки с баком М, за время спуска вытекает лишь небольшая часть воды. [
|
:
. Знайти через 2 с:
]
10.2. Тело массой m бросили под углом к горизонту с начальной скоростью vo. Пренебрегая сопротивлением воздуха, найти приращение импульса тела за первые t секунд движения. [ 
]
]
]
]
]
]
раз больше]
; б) 
]
; б) 
; в) 
]
]
]
]
]
]
]
б) 
в) 0]
; если;
; 
, если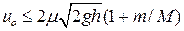 
]
10.28. Два бруска массами m1 и m2 висят на невесомой нити, перекинутой через неподвижный невесомый блок. Найти ускорение центра масс системы при свободном движении брусков. Трения нет. [ 
]
10.30. На лодке находится массивный вал, на который намотан канат (рис. 10.3). За канат тянут с постоянной и одинаковой силой в двух случаях: когда вал зажат и когда он может свободно вращаться. В каком случае лодка будет двигаться быстрее? Сопротивление не учитывать. [одинаково]
]
, если 
]
]
]
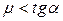10.38. На вертикальном стержне AB нарезана резьба (рис. 10.4). На него навернут горизонтальный стержень CD. Стержень CD отпускают и он под действием силы тяжести скручивается со стержня AB. Как будет двигаться стержень CD после того как слетит с винта? [двигаться как горизонтально брошенное тело, одновременно вращаясь вокруг своего центра]
]
]
]
]
]
]
]
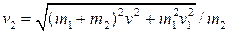, под углом к направлению снаряда равным 
]
]
]
]