 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Основные свойства двойного интеграла.
Двойные и тройные интегралы Двойной интеграл Основные понятия и определения Обобщением определенного интеграла в случае функции двух переменных является так называемый двойной интеграл.  Пусть в замкнутой области D плоскости Оху задана непрерывная функция Пусть в замкнутой области D плоскости Оху задана непрерывная функция  . Разобьем область D на n «элементарных областей» . Разобьем область D на n «элементарных областей»  , площади которых обозначим через , площади которых обозначим через 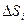 , а диаметры (наибольшее расстояние между точками области) – через , а диаметры (наибольшее расстояние между точками области) – через  (см.рис.1). (см.рис.1).
В каждой области  выберем произвольную точку выберем произвольную точку  , умножим значение , умножим значение  функции в этой точке на функции в этой точке на 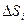 и составим сумму всех таких произведений: и составим сумму всех таких произведений: 
Эта сумма называется интегральной суммой функции f(x;y) в области D. Рассмотрим предел интегральной суммы  , когда n стремится к бесконечности таким образом, что , когда n стремится к бесконечности таким образом, что  . Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается . Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается  (или (или  ) ) Таким образом, двойной интеграл определяется равенством 
В этом случае функция f(x;y) называется интегрируемой в области D; D – область интегрирования; x и y – переменные интегрирования. Теорема(достаточное условие интегрируемости функции). Если функция z=f(x;y) непрерывна в замкнутой области D, то она интегрируема в этой области. Объем цилиндрического тела 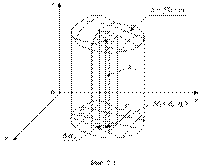 Рассмотрим тело, ограниченное сверху поверхностью Рассмотрим тело, ограниченное сверху поверхностью  , снизу – замкнутой областью D плоскости Оху, боковое ограничение- цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см.рис.2.1). , снизу – замкнутой областью D плоскости Оху, боковое ограничение- цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см.рис.2.1).
Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z=f(x;y) на плоскость Оху) произвольным образом на n областей  , площади которых равны , площади которых равны  . Рассмотрим цилиндрические столбики с основаниями . Рассмотрим цилиндрические столбики с основаниями  , ограниченные сверху кусками поверхности z=f(x;y). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием , ограниченные сверху кусками поверхности z=f(x;y). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием  через через  , получим. , получим. 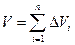
Возьмем на каждой площадке  произвольную точку произвольную точку  и заменим каждый столбик прямым цилиндром с тем же основанием и заменим каждый столбик прямым цилиндром с тем же основанием  и высотой и высотой  . Объем этого цилиндра приблизительно равен объему . Объем этого цилиндра приблизительно равен объему  цилиндрического столбика, т.е. цилиндрического столбика, т.е.  . Тогда получаем: . Тогда получаем: 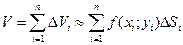
Это равенство тем точнее, чем больше число n и чем меньше размеры «элементарных областей»  . Естественно принять предел суммы . Естественно принять предел суммы 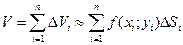 при условии, что число площадок при условии, что число площадок  неограниченно увеличивается неограниченно увеличивается  , а каждая площадка стягивается в точку ( , а каждая площадка стягивается в точку (  ), за объем V цилиндрического тела, т.е. ), за объем V цилиндрического тела, т.е.  , или, согласно равенству , или, согласно равенству  . . Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. Основные свойства двойного интеграла. 1.  , c-const. , c-const. 2.  3. Если область D разбить линией на 2 области  и и  такие, что такие, что  , а пересечение , а пересечение  и и  состоит лишь из линии, их разделяющей, то состоит лишь из линии, их разделяющей, то 
4. Если в области D имеет место неравенство  , то и , то и  . Если в области D функции . Если в области D функции  и и  удовлетворяют неравенству удовлетворяют неравенству  , то и , то и  5.  , так как , так как  6. Если функция  непрерывна в замкнутой области D, площадь которой S, то непрерывна в замкнутой области D, площадь которой S, то  , где m и M – соответственно наименьшее и наибольшее значения подынтегральной функции в области D. , где m и M – соответственно наименьшее и наибольшее значения подынтегральной функции в области D. 7. Если функция  непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка 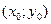 , что , что  . .
Величину называют средним значением функции в области D
|




 Пусть в замкнутой области D плоскости Оху задана непрерывная функция
Пусть в замкнутой области D плоскости Оху задана непрерывная функция  . Разобьем область D на n «элементарных областей»
. Разобьем область D на n «элементарных областей»  , площади которых обозначим через
, площади которых обозначим через 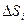 , а диаметры (наибольшее расстояние между точками области) – через
, а диаметры (наибольшее расстояние между точками области) – через  (см.рис.1).
(см.рис.1). выберем произвольную точку
выберем произвольную точку  , умножим значение
, умножим значение  функции в этой точке на
функции в этой точке на 
 . Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается
. Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается  (или
(или  )
)
 Рассмотрим тело, ограниченное сверху поверхностью
Рассмотрим тело, ограниченное сверху поверхностью  , снизу – замкнутой областью D плоскости Оху, боковое ограничение- цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см.рис.2.1).
, снизу – замкнутой областью D плоскости Оху, боковое ограничение- цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см.рис.2.1). . Рассмотрим цилиндрические столбики с основаниями
. Рассмотрим цилиндрические столбики с основаниями  , получим.
, получим.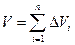
 . Объем этого цилиндра приблизительно равен объему
. Объем этого цилиндра приблизительно равен объему  . Тогда получаем:
. Тогда получаем: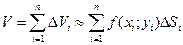
 , а каждая площадка стягивается в точку (
, а каждая площадка стягивается в точку (  , или, согласно равенству
, или, согласно равенству  .
. , c-const.
, c-const.
 и
и  такие, что
такие, что  , а пересечение
, а пересечение 
 , то и
, то и  . Если в области D функции
. Если в области D функции  и
и  удовлетворяют неравенству
удовлетворяют неравенству  , то и
, то и 
 , так как
, так как 
 , где m и M – соответственно наименьшее и наибольшее значения подынтегральной функции в области D.
, где m и M – соответственно наименьшее и наибольшее значения подынтегральной функции в области D.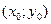 , что
, что  .
.