 ПОЗНАВАТЕЛЬНОЕ
| Вычисление тройного интеграла в декартовых координатах
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов. Пусть областью интегрирования V является тело, ограниченное снизу поверхностью
сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного. При этом сначала вычисляется внутренний интеграл по переменной z при постоянных х и у в пределах изменения z. Нижней границей интеграла является Если область D ограничена линиями x=a, x=b (a<b),
по которой вычисляется тройной интеграл в декартовых координатах.
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.
При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т.е. совершается преобразование переменных. Пусть совершена подстановка Если эти функции имеют в некоторой области
то справедлива формула замены переменных в тройном интеграле:
Здесь
Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты. Положение точки M(x;y;z) в пространстве Oxyz можно определить заданием трех чисел r,
Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:
( Возьмем в качестве u, v, w цилиндрические координаты r,
Формула замены переменных принимает вид
Таким образом, вычисление тройного интеграла приводится к интегрированию по r, по
Сферическими координатами точки М(x;y;z) пространства Oxyz называется тройка чисел
Сферические координаты
( В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Для этого нужно воспользоваться формулой замены переменных в тройном интеграле. Так как якобиан преобразования
то
|



 , сверху – поверхностью
, сверху – поверхностью  , причем
, причем  и
и  - непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость Oxy. Будем считать область V – правильной в направлении оси Oz: любая прямая, параллельная оси Oz, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области V функции
- непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость Oxy. Будем считать область V – правильной в направлении оси Oz: любая прямая, параллельная оси Oz, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области V функции 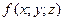 имеет место формула
имеет место формула ,
, и
и  , где
, где  и
и  – непрерывные на отрезке [a;b] функции, причем
– непрерывные на отрезке [a;b] функции, причем  , то, переходя от двойного интеграла по области D к повторному, получаем формулу
, то, переходя от двойного интеграла по области D к повторному, получаем формулу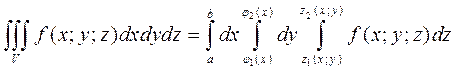 ,
, ,
,  ,
, 
 пространства Ouvw непрерывные частные производные и отличный от 0 определитель
пространства Ouvw непрерывные частные производные и отличный от 0 определитель ,
,
 – определитель Якоби, или якобиан преобразования.
– определитель Якоби, или якобиан преобразования. ,z, где r – длина радиус-вектора проекции точки М на плоскость Оху,
,z, где r – длина радиус-вектора проекции точки М на плоскость Оху, 
 ;
;  ;
; 
 ;
;  ;
;  )
)

 , где
, где  – длина радиус-вектора точки М,
– длина радиус-вектора точки М,  на плоскость Оху и осью Ох,
на плоскость Оху и осью Ох, - угол отклонения радиус-вектора
- угол отклонения радиус-вектора  ,
,  ,
,  .
. ;
;  ;
;  )
)

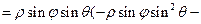
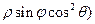

 ,
, .
.