 ПОЗНАВАТЕЛЬНОЕ
| Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки, т.е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у как
Если эти функции имеют в некоторой области
а функция
Функциональный определитель
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами r и В качестве u и v возьмем полярные координаты r и
Правые части в этих равенствах – непрерывно дифференцируемые функции.
Якобиан преобразования определяется как
Формула замены переменных принимает вид:
Где Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если область
(ограничена лучами Внутренний интеграл берется при постоянном
Тройной интеграл.
Основные понятия.
Обобщением определенного интеграла на случай функции трех переменных является так называемый тройной интеграл. Теория тройного интеграла аналогична теории двойного интеграла.
Пусть в замкнутой области V пространства Oxyz задана непрерывная функция Если предел интегральной суммы существует при неограниченном увеличении числа n таким образом, что каждая «элементарная область» или
Таким образом, по определению, имеем:
Здесь dv=dxdydz – элемент объема.
Теорема(существования). Если функция
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:
1. 2. 3. 4. 5. 6.Оценка тройного интеграла:
где m и M – соответственно наименьшее и наибольшее значения функции 7. Теорема о среднем значении: если функция
|



 и
и 
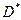 плоскости Ouv непрерывные частные производные первого порядка и отличный от 0 определитель
плоскости Ouv непрерывные частные производные первого порядка и отличный от 0 определитель ,
, непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
 .
. и
и  .
.
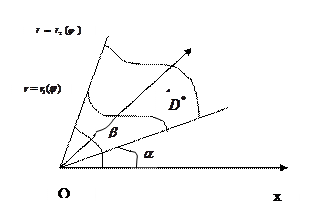
 ,
,
 и
и  , где
, где  , и кривыми
, и кривыми  и
и  , где
, где  , т.е. область
, т.е. область 
 . Разбив область V сеткой поверхностей на n частей
. Разбив область V сеткой поверхностей на n частей  и выбрав в каждой из них произвольную точку
и выбрав в каждой из них произвольную точку  , составим интегральную сумму
, составим интегральную сумму  для функции
для функции 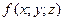 по области V.
по области V. стягивается в точку (т.у. диаметр области
стягивается в точку (т.у. диаметр области  стремится к нулю, т.е.
стремится к нулю, т.е.  ), то его называют тройным интегралом от функции
), то его называют тройным интегралом от функции 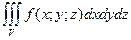
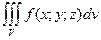

 и
и  существует и не зависит ни от способа разбиения области V на части, ни от выбора точек
существует и не зависит ни от способа разбиения области V на части, ни от выбора точек  ,
, 

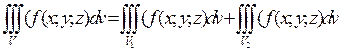 ,если V =
,если V =  , а пересечение
, а пересечение  и
и  состоит из границы, их разделяющей.
состоит из границы, их разделяющей.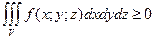 , если в области V функция
, если в области V функция  . Если в области интегрирования
. Если в области интегрирования  , то и
, то и 
 , так как в случае
, так как в случае  любая интегральная сумма имеет вид
любая интегральная сумма имеет вид  и численно равна объему тела.
и численно равна объему тела. ,
, , что
, что  , где V – объем тела,
, где V – объем тела,