 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Уравнения, приводимые к линейным.
Несложные уравнения с параметром, при решении которых требуется дополнительная проверка, связанная с ограничениями их области определения, составляет следующий шаг в изучении уравнений с параметром. Пример1. Решите уравнение Решение. Очевидно, что х ≠ 2. Умножив обе части уравнения на х–2≠0, получим а = х – 2 или х = а + 2. Проверим, нет ли таких значений параметра а, при котором найденное значение х было бы равно числу 2, то есть решим уравнение 2 = а + 2 относительно а. Получим, что при а = 0 х =2, но число 2 не входит в область определения, следовательно, не может быть его корнем. Ответ: при а = 0 корней нет; при а≠ 0 х = а +2. Пример2. Решите уравнение Решение: х ≠ –1. Приведя уравнение к виду (1 — а)х = а, заметим, что при а = 1 уравнение не имеет корней, а при а ≠1 получаем Ответ: при а ≠1 Пример 3. Решите уравнение Решение После преобразований получаем уравнение 2ах =1– а, которое при а = 0 не имеет корней, а при а ≠ 0 – 0,2, корень второго уравнения 0,2, то есть при а ± 0, 2 соответствующие значения х не входят в область определения исходного уравнения. Ответ: при Пример 4. Исследовать и решить уравнение с параметром.
D(у): х≠ -1. kx + 2k – 3k + 3 = x + 1; (k – 1 )x = x + 1 - вид уравнения наиболее удобный для исследования.
б) Выясним, при каких значениях параметра k х = -1, и исключим их. Для этого решим уравнение:
в) Если k = 1, то 0х = -1, решений нет.
1 1,5 k
k ≠1,5 существует ед. х = 2) При k =1 решений нет. 3) При k = 1,5 решений нет. Пример 5. Исследовать и решить уравнение с параметром.
x≠-3. Преобразуем данное уравнение в равносильное с учётом D (у): 3mx – 5 + (3m – 11)(x + 3) = (2x + 7)(m – 1); (4m – 9)x = 31 – 2m - линейное уравнение с параметром, удобное для исследования.
m ≠ 1 , то существует ед. б) Выясним, при каких значениях параметра m x = -3.
в) Если m = 2,25, то 0х = 26,5, следовательно, решений нет.
-0,4 1 2,25 m 1) 3) 4) 2)
m ≠ - 0,4 существует ед. m ≠ 1 2) При m = 2,25 решений нет 3) При m = - 0,4 решений нет 4) При m = 1 уравнение не определено или не имеет смысла. Пример 6. Исследовать и решить уравнение с параметром.
D(y):
а) Если б) в) г) Графическая иллюстрация исследования c параметром m
m
5) 1) 4) 3) 2) Ответ: 1) При 2) При 3) При 4) При 5) При Пример 7. Исследовать и решить уравнение с параметром: D(y) : Данное уравнение перепишем в виде
а) Если б) Выясним, при каких значениях параметра m x=1, и исключим эти значения, т.е. в) Если m=1, то, г) Если m = -1, то д) Если m = 0 - уравнение не определено. Ответ: а) а) Если б) Если m=1, то для любого x ≠ 1 есть решение. в) Если m = -1, решений нет г) Если m = 0 - уравнение не определено. Пример 8. Исследовать и решить уравнение с параметром: Найдём область определения данного уравнения. D(y) : х ≠±1. Запишем уравнение в виде. а) Если а ≠ -2 , то существует ед. х б) Выясним, при каких значениях параметра а х=1, и исключим их.
в) выясним, при каких значениях параметра а х=-1,
г) Если а = -2, то Графическая иллюстрация исследования c параметром а
а
1) 2) 3) Ответ 1) При 2) При а = -2, решений нет. 3) При а = 1, решений нет. Пример 9. Исследовать и решить уравнение с параметром
D(y): Запишем уравнение в виде а) Если б) Выясним, при каких значениях параметра m x=-3.
в) Если m = -4, то г) Если m = 2, то д) Если m = -1 – уравнение не определено. Ответ: 1) При 2) При m = - 4, любое х ≠-3 есть решение. 3) При m = 2, решений нет. 4) При m = -1 – уравнение не определено Пример 10. Исследовать и решить уравнение с параметром
D (y): Запишем уравнение в виде
а) Если б) Если а=0, то 0=0, следовательно, любое х из области определения есть решение. Ответ: 1) При 2) При а=0, любое х ≠ 1 – есть решение. 3) При а = 1,5 уравнение не определено. Пример 11. Исследовать уравнение, выяснить, при каких значениях параметра m существует единственное решение, меньше 1.
D(y): Запишем уравнение в виде
I. а) Если б) Выясним, при каком значении параметра m х=-2.
в) Выясним, при каком значении параметра m х=-3
II. Решим неравенство Графическая иллюстрация:
m Ответ: при Пример 12. Исследовать уравнение, выяснить при каких значениях параметра m существует единственное положительное решение. D(y) Запишем уравнение в виде I. а) Если б) Выясним, при каком значении параметра m
в) При Тогда уравнение имеет вид
II. Графическая иллюстрация:
m Ответ: при Пример 13. Исследовать и решить уравнение с параметром
D (y): В результате преобразований получаем а) Если б) Выясним при каком значении параметра b в) Выясним при каком значении параметра b г) Если Ответ: 1)При 2) При 4) При Пример 14. Исследовать и решить уравнение с параметром
D(y): Преобразуем уравнение в более удобное для исследования.
а) Если б) Выясним, при каком значении параметра n х=0.
в) Если г) Если д) Если Ответ: 1) При 2) При 3) При 4) При Заключение. Для реализации проекта мною были проанализированы методическая литература и учебные пособия, которые позволили выявить основные методы решения линейных уравнений с параметрами и адаптировать их к школьному курсу. Что помогло составить систему дидактических материалов, которые можно использовать для учащихся 7 – 11 классов в процессе усвоения той или иной темы или для параллельного повторения при подготовке к ГИА или ЕГЭ.
Список литературы: 1. Натяганов В.Л., Лужина Л.М. Методы решения задач с параметрами: Учеб. пособие. – М.: Изд-во МГУ, 2003. – 368 с. 2. Шахместер А.Х. Уравнения и неравенства с параметрами. – 1-е изд.– СПб.: «ЧеРо-на-Неве», 2004.– 304с. 3. Шахместер А.Х. Задачи с параметрами в ЕГЭ. – 1-е изд.– СПб.: «ЧеРо-на-Неве», 2004.– 304с. 4. Шахместер А.Х. Задачи с параметрами на экзаменах. – 3-е изд., исправленное.– М.: Издательство МЦНМО: СПб.: «Петроглиф»: «Виктория плюс»,2009. – 248с. 5. Н.Воронина Уравнения с параметрами на уроках повторения. – Газета «Математика» №1/ 2010г. Издательский дом «Первое сентября». 6. Т.Овчинникова, Факультативный курс «Линейные уравнения и неравенства с параметрами» – Газета «Математика» №1/ 2010г. №2/2010, №3/2010 Издательский дом «Первое сентября». 7. П.И. Горнштейн, В.Б. Полонский, М.С. Якир Задачи с параметрами. 3-е издание, дополненное и переработанное. – М.: Илекса, Харьков: Гимназия, 1999 – 336с. 8. Алгебра. 8 класс. В 2 ч. /[А.Г.Мордкович и др.] под ред. А.Г. Мордковича. – 11-е изд. Стер. М.: Мнемозина, 2009. 9. Алгебра. 9 класс. В 2 ч. /[А.Г.Мордкович и др.] под ред. А.Г. Мордковича. – 11-е изд. Стер. М.: Мнемозина, 2009. 10. Алгебра. 10-11 класс. В 2 ч. /[А.Г.Мордкович и др.] под ред. А.Г. Мордковича. – 11-е изд. Стер. М.: Мнемозина, 2009. 11. Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену. – 9-е изд.- М.: Айрис-пресс, 2004 – 432с. 12. Субханкулова С.А. Задачи с параметрами. – М.: ИЛЕКСА, 2010. – 208с (Серия «Математика: элективный курс»). |





 . Решим уравнение
. Решим уравнение  относительно а. Так как уравнение не имеет корней, других вариантов не имеется.
относительно а. Так как уравнение не имеет корней, других вариантов не имеется.
 При условии, что
При условии, что  исходное уравнение можно упростить:
исходное уравнение можно упростить: 
 . Проверим, нет ли таких значении параметра а, при которых найденное значение х было бы равно – 3 или 2. для этого решим относительно а уравнения
. Проверим, нет ли таких значении параметра а, при которых найденное значение х было бы равно – 3 или 2. для этого решим относительно а уравнения  . Корень первого уравнения
. Корень первого уравнения корней нет; при
корней нет; при 

 a) Пусть k ≠ 1, тогда существует единственный х
a) Пусть k ≠ 1, тогда существует единственный х  .
. , тогда k = 1,5.
, тогда k = 1,5. Графическая иллюстрация исследования по параметру k
Графическая иллюстрация исследования по параметру k
 Ответ: 1) При k ≠ 1
Ответ: 1) При k ≠ 1 .
.
 D (у): m ≠ 1
D (у): m ≠ 1 а) Если m ≠ 2,25
а) Если m ≠ 2,25
 следовательно, m = - 0,4, т.е. при m = - 0,4 х
следовательно, m = - 0,4, т.е. при m = - 0,4 х  .
. Графическая иллюстрация исследования по параметру
Графическая иллюстрация исследования по параметру Ответ: 1) при m ≠ 2,25
Ответ: 1) при m ≠ 2,25

 Выполнив необходимые преобразования получим следующее уравнение:
Выполнив необходимые преобразования получим следующее уравнение: 
 .
. то
то 

 тогда
тогда  т.е.
т.е. 
 тогда
тогда  т.е.
т.е. 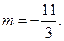
 тогда 0= - 6,5, следовательно, решений нет
тогда 0= - 6,5, следовательно, решений нет
 - 2
- 2  -1,5
-1,5 существует единственное решение
существует единственное решение 
 решений нет
решений нет решений нет
решений нет уравнение не определено.
уравнение не определено. решений нет.
решений нет.

 или
или 
 то существует ед.
то существует ед. 
 или 2 = 1. Следовательно, не существует такого значения параметра m, при котором x=1, т.е. дополнительных ограничений на значение параметра m нет.
или 2 = 1. Следовательно, не существует такого значения параметра m, при котором x=1, т.е. дополнительных ограничений на значение параметра m нет. следовательно, любое
следовательно, любое  есть решение уравнения, т.е. это случай бесконечного множества решений.
есть решение уравнения, т.е. это случай бесконечного множества решений. , т.е. решений нет.
, т.е. решений нет.

 или
или 

 , т.е. а = 1.
, т.е. а = 1. , т.е. 4=-2, или решений нет. Следовательно, не существует такого значения параметра а, при котором х=-1.
, т.е. 4=-2, или решений нет. Следовательно, не существует такого значения параметра а, при котором х=-1. , т.е. решений нет.
, т.е. решений нет. -2 1
-2 1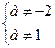 существует ед. х
существует ед. х 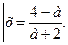

 .
. , или
, или 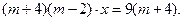
 то существует ед. х
то существует ед. х 
 т.е. m ≠-1.
т.е. m ≠-1. , следовательно, любое х из области определения уравнения есть решение.
, следовательно, любое х из области определения уравнения есть решение. , т.е решений нет.
, т.е решений нет.
 .
.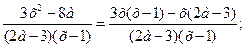


 то существует ед. х
то существует ед. х  .
.



 то существует ед. х
то существует ед. х 
 т.е.
т.е. 
 т.е.
т.е.  .
. . Перенесём 1 в левую часть, тогда
. Перенесём 1 в левую часть, тогда 

 0
0 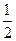 1
1 
 существует единственное решение
существует единственное решение  такое, что
такое, что 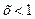 .
.
 .
.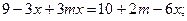
 .
.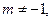 то существует ед. х
то существует ед. х 

 тогда
тогда 
 найдём дополнительное ограничение на значение параметра m.
найдём дополнительное ограничение на значение параметра m.
 т.е.
т.е. 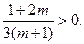
 -2 -1 -½
-2 -1 -½ существует ед. х
существует ед. х 


 - данное уравнение наиболее удобно для исследования.
- данное уравнение наиболее удобно для исследования. то существует ед. х
то существует ед. х 
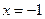

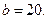


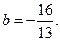
 , то
, то  решений нет.
решений нет. существует ед. х
существует ед. х  решений нет.
решений нет. решений нет.
решений нет.


 .
. то существует ед х
то существует ед х 

 .
. , то
, то  любое значении х из области определения является решением.
любое значении х из области определения является решением. , уравнение не определено.
, уравнение не определено. является решением.
является решением.