 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Частные случаи решения линейных уравнений
Ученики должны понять, что решение уравнения с параметрами при заданных конкретных условиях – это частные решения уравнений. Например, задание может звучать так: «При каких значениях параметра … уравнение …. Имеет единственное решение или не имеет корней, или имеет корень равный… и т.д. Пример1. При каких целых значениях параметра а уравнение Решение: Приведём уравнение к виду Ответ: при а = -3; 1; 3; 7 . Пример 2. При каких значениях параметра n уравнение а) имеет единственный корень; б) имеет бесконечное множество корней; в) не имеет корней. Решение: 1. Выражения 2. Если 3. При Ответ: а) При б) При Пример 3. При каком значении параметра а уравнение не имеет корней Перепишем данное уравнение в виде Пример 4. Найдите все значения параметра а, при каждом из которых число 7 является единственным корнем уравнения. Решение: Способ I: Если для некоторого значения параметра число 7 является корнем уравнения, то для этого значения а справедливо равенство Равенство справедливо при а = 0 или при а =1. Внимание! Мы ещё не получили ответа, так как нашли два значения параметра а, предполагая, что число 7 является корнем уравнения. Но этот корень должен быть единственным, поэтому ещё требуется проверить, является ли число 7 единственным корнем уравнения при а = 0 или при а =1. Если а = 0, то уравнение перепишем в виде х – 7 = 0. При а = 0 число7 является единственным корнем уравнения. Если же а =1, то уравнение перепишем в виде х - 7 = х – 7. При а=1 любое действительное число является корнем данного уравнения. Следовательно, число 7 не является единственным корнем уравнения . Способ II. Перепишем исходное уравнение в виде При а =1 корнем уравнения является любое число, то есть число 7 не является единственным корнем уравнения. Поэтому в уравнении а ≠1. Но тогда это уравнение имеет единственный корень Ответ: а = 0. Пример 5. Найдите все значения параметра а, при каждом из которых уравнения Решение: Перепишем первое уравнение в виде Перепишем второе уравнение в виде Осталось найти все значения параметра Для этого решим уравнение Перенесём все слагаемые в одну часть уравнения и упростим разность алгебраических дробей, равносильное уравнение Ответ: при 4. Аналитический и графический способы решения линейных уравнений Пример 1.Решите уравнение Решение: Способ 1. (аналитический). 1. При а>0 уравнение имеет два корня: 2. При а=0 уравнение имеет один корень: х=0 3. При а<0 уравнение корней не имеет. Способ II.(графический) 1. При а>0 графики пересекаются в двух точках ( – а; а) и ( а; а), значит уравнение имеет два решение:
2. При а=0 точка пересечения графиков одна – начало координат, следовательно, уравнение имеет одно решение: х=0. 3. При а<0 графики функции не пересекаются – решений нет. Ответ: при а<0 корней нет; при а=0 один корень: х=0; при а>0 два корня: Пример 2.Решите уравнение Решение. Способ I (аналитический). 1. При а) при а ≠ 1 уравнение имеет только одно решение: х = 0; б) при а = 1 уравнение имеет бесконечное множество решений: 2. При х ≤ 0 уравнение равносильно уравнению ах = — х, или х(а + 1) = 0. Следовательно: а) при а ≠ —1 уравнение имеет одно решение: х = 0; б) при а = —1 - множество решений, Способ II (графический).
у А В
х
1. При 2. При а = 1 прямая у = х содержит луч ОА, и уравнение имеет бесконечное множество решений З. При а = —1 прямая у = х содержит луч ОВ, и уравнение имеет бесконечное множество решений Ответ: при а = —1 Пример 3. Решите уравнение | х + 2| = ах + 1. Решение аналитическим способом приводит к достаточно длительным рассуждениям, так как имеет много ветвлений. Графический способ более удобен, он короче и красивее. Решение. Построим график функций у =| х + 2| и у = ах + 1. График первой функции получается сдвигом графика функции у =| х| на 2 единицы влево по оси абсцисс. Графиком второй функции является прямая, проходящая через точку с координатами (0; 1), угловой коэффициент которой равен а. Рассматривая график функции у = ах + 1 при различных числовых значениях параметра а, получаем пучок прямых, проходящих через точку (0; 1).
Если угловой коэффициент Если При При Таким образом, получаем ответ. Ответ: При При |



 имеет целые корни.
имеет целые корни. , если
, если  то
то  . Чтобы х был целым числом, необходимо, чтобы значение выражения
. Чтобы х был целым числом, необходимо, чтобы значение выражения  было делителем числа 5, то есть
было делителем числа 5, то есть 
 имеют смысл при любых значениях n/
имеют смысл при любых значениях n/ , то
, то  . При
. При 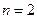 значение выражения
значение выражения  равно 0. Получаем уравнение вида
равно 0. Получаем уравнение вида  . Оно имеет бесконечное множество корней, то есть х – любое число. При
. Оно имеет бесконечное множество корней, то есть х – любое число. При 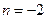 значение выражения
значение выражения  , которое не имеет корней.
, которое не имеет корней.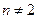 и
и  уравнение имеет единственный корень.
уравнение имеет единственный корень. .
. Если а = 2, то уравнение не имеет корней. Ответ: а = 2
Если а = 2, то уравнение не имеет корней. Ответ: а = 2 , или равенство
, или равенство  .
.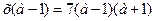
 . Условие задачи будет выполнено, если это единственный корень есть число 7:
. Условие задачи будет выполнено, если это единственный корень есть число 7:  то есть при а = 0.
то есть при а = 0. и
и  имеют общий корень.
имеют общий корень. . Это уравнение имеет корень лишь при
. Это уравнение имеет корень лишь при  . Этот корень есть число
. Этот корень есть число  .
. . Данное уравнение имеет корень лишь при
. Данное уравнение имеет корень лишь при  ,. Этот корень есть число
,. Этот корень есть число 
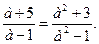
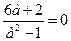 которое имеет единственный корень
которое имеет единственный корень 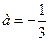 . При этом значении а условие задачи выполнено.
. При этом значении а условие задачи выполнено. .
. .
. у
у 
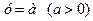
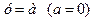 х
х
 .
. уравнение равносильно уравнению ах = х, или х(а — 1) = 0. Следовательно:
уравнение равносильно уравнению ах = х, или х(а — 1) = 0. Следовательно:

 Построим графики функций
Построим графики функций  . Графиками функций у = ах являются прямые, проходящие через начало координат, угловой коэффициент которых равен а.
. Графиками функций у = ах являются прямые, проходящие через начало координат, угловой коэффициент которых равен а.




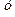
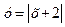












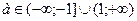 , то есть прямые проходят в области 1, то они пересекает правую ветвь (х > –2) графика функции
, то есть прямые проходят в области 1, то они пересекает правую ветвь (х > –2) графика функции  , то прямые проходят в области 2, и графики функций пересекаются в двух точках, то есть уравнение имеет два решения.
, то прямые проходят в области 2, и графики функций пересекаются в двух точках, то есть уравнение имеет два решения. прямые расположены в области 3, в этом случае графики функций не пересекаются, следовательно, уравнение решений не имеет.
прямые расположены в области 3, в этом случае графики функций не пересекаются, следовательно, уравнение решений не имеет. точка пересечения одна, и решение тоже одно.
точка пересечения одна, и решение тоже одно.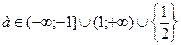 уравнение имеет одно решение;
уравнение имеет одно решение;