 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Разработка методических рекомендаций решения линейных уравнений и неравенств с параметрами.
Разработка методических рекомендаций Решения линейных уравнений с параметрами.
Работа выполнена: учителем математики МОУ СОШ №75 г.Черноголовка Аветисян Еленой Владимировной
Научный руководитель: к.п.н., доцент Ерина Татьяна Михайловна
Москва 2011г. Содержание проекта: Вступление 1. Алгоритм решение линейных уравнений с параметрами. 2. Решение простейших уравнений с параметрами. 3. Частные случаи решения линейных уравнений. 4. Аналитический и графический способы решения линейных уравнений 5. Уравнения, приводимые к линейным. 6. Заключение. 7. Список литературы. Разработка методических рекомендаций решения линейных уравнений и неравенств с параметрами. Математику затем учить следует, что она ум в порядок приводит. М.В.Ломоносов. Всё возрастающая популярность задач с параметрами далеко не случайна. Теоретическое изучение и математическое моделирование многообразных процессов из различных областей науки и практической деятельности человека часто приводят к достаточно сложным уравнениям и неравенствам или их системам содержащим параметры. Задачи с параметрами, предлагающиеся на конкурсных экзаменах, являются прообразом важных научно-исследовательских задач, которые предстоит решать будущему поколению. Такие задачи требуют глубокого понимания сути процесса, свободного владения различными математическими методами и скрупулёзного анализа. Программа по математике средней общеобразовательной школы не уделяет большого внимания решению задач с параметрами. Следовательно, каждый учитель должен сам найти время на уроке для решения таких задач. Эти задачи представляют чисто математический интерес, способствуют интеллектуальному развитию учащихся, служат хорошим материалом для отработки навыков. Все рассмотренные задания в данной работе имеют цель – помочь учащимся составить представление о параметре, о том, что значит решить уравнение с ним. В самом начале знакомства с параметрами у учеников возникает психологический барьер, который обусловлен его противоречивыми характеристиками. С одной стороны, параметр в уравнении следует считать величиной известной, а с другой, конкретное значение параметра не дано. С одной стороны, параметр является величиной постоянной, а с другой может принимать различные значения. Получается, что параметр в уравнении – это «неизвестная величина», «переменная постоянная». Эти противоречивые высказывания точно отражают суть тех сложностей, которые нужно преодолеть ученикам. Цель проекта: Разработать методические рекомендации использования современных технологий при обучении решению линейных уравнений с параметрами. Задачи проекта: 1. Провести обзор методической литературы, методических пособий, учебников, методических разработок по данной теме. 2. Выявить наиболее общие подходы к решению линейных уравнений с параметрами. 3.Сформировать понимание основных методов решения линейных уравнений с параметрами. 4. Раскрыть значение заданий с параметрами в системе школьного образования.
Долгий путь начинается с первого шага. (восточная мудрость)
1. Алгоритм решения линейных уравнений с параметрами. Исследовать и решить уравнение с параметром – это значит: 1. Найти все системы значений параметров, при которых данное уравнение имеет решение. 2. Найти все решения для каждой найденной системы значений параметров, т.е. для неизвестного и параметра должны быть указаны свои области допустимых значений. На экзаменах встречаются, в основном, два типа задач с параметрами. I. Для каждого значения параметра найти все решения некоторого уравнения и неравенства. II. Найти все значения параметра, при каждом из которых для данного уравнения и неравенства выполняются некоторые условия.
Определение:Уравнение вида Алгоритм решения: 1. Найти допустимые значения параметра. 2. Если 3. Если Учащимся можно данный алгоритм предложить оформить в виде таблицы. Алгоритм решения линейных уравнений с параметрами.
|
, где 
- некоторые аналитические выражение, называется линейным относительно переменной х спараметром а. Если поставлена задача решить такое уравнение, это значит, для каждого допустимого значения параметра а надо найти значение переменной х, удовлетворяющее этому уравнению.
, то существование или отсутствие корней зависит от значения 
Если 
то уравнение принимает вид 
и его корнем служит любое действительное значение переменной х. Если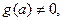 
то при любом значении переменной х возникает неверное числовое равенство, то есть уравнение корней не имеет.
то получим, что 
или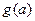 
не имеют смысла
