 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Общая схема выборочного эксперимента
По эмпирическим данным, представляющим собой выборку из некоторой генеральной совокупности, оцениваются параметры, позволяющие описать всю генеральную совокупность; определяется интервал, в котором с заданным уровнем доверия находится истинное значение оцениваемого параметра; а затем про-веряются те или иные утверждения и делаются выводы о свойствах всей генеральной совокупности. 2.5. Эмпирическая функция распределения, гистограмма
Определение 1. Эмпирической функцией распределения, построенной по выборке
Выборка:
Эмпирическая функция распределения имеет скачки в точках выборки, величина скачка в точке Можно построить эмпирическую функцию распределения по вариационному ряду:
Другой характеристикой распределения является таблица (для дискретных распределений) или плотность (для абсолютно непрерывных). Эмпирическим, или выборочным аналогом таблицы или плотности является так называемая гистограмма. Гистограмма строится по группированным данным. Предполагаемую область значений случайной величины
Пример 2. Имеется вариационный ряд (см. пример 1):
Разобьем отрезок
2.6 Описательная статистика. Рассмотрим один из самых интересных методов: описательная статистика. Описательная статистика –это раздел статистики, занимающийся описанием организацией и простейшим преобразованием данных исследования. О назначении описательной статистики можно судить по ее названию: она имеет дело с числами, характеризующими ту или иную интересующую нас ситуацию. Вот примеры статистической информации: • уровень преступности в регионе; Ценность описательной статистики заключается прежде всего в том, что она дает сжатую и концентрированную характеристику изучаемого явления. Рассмотрим следующий пример. Пусть на некотором предприятии работает 1500 человек. Бухгалтерская ведомость на зарплату довольно большая. Информация о том, что средняя месячная зарплата работников этого предприятия составляет 8200 рублей, дает определенное, хотя и неполное представление об уровне заработной платы на этом предприятии. Предмет исследований во многих сферах отличается исключительной сложностью, изменчивостью, индивидуальным многообразием явлений и процессов. Эти процессы происходят неоднозначно. Поэтому применение одинаковых подходов, средств, технологий дает в каждом конкретном случае различные результаты в зависимости от субъективных факторов, от обстоятельств, которые нельзя контролировать и которые влияют на протекание процесса. Неоднозначность протекания процесса порождается наличием присущего ему случайного. Но это не означает отсутствие общих закономерностей в изучаемых процессах и явлениях. Например, невысокая скорость чтения у отдельного учащегося является случайным событием, но у ученика, любящего читать, она встречается существенно реже, чем у того, кто редко берет книгу в руки. Эта устойчивость появления тех или других случайных событий уже является закономерностью. Информационная функция описательной статистики состоит из сбора, обобщения и представления всем заинтересованным лицам достоверной, своевременной информации об исследуемом явлении. В связи с тем, что иногда исследованию подлежат тысячи объектов, необходимым является переход от сплошного изучения к выборочному по многим показателям. Поэтому важное значение приобретают технологии сбора, обработки и анализа данных, которые позволяют использовать информационные возможности частичных первоначальных данных для разработки обобщенной информации о том или ином процессе.
2.7 Теория оценивания Статистическое оценивание совокупность способов, употребляемых в математической статистике (См. Математическая статистика) для приближённого определения неизвестных распределений вероятностей (или каких-либо их характеристик) по результатам наблюдений. В наиболее распространённом случае независимых наблюдений их результаты образуют последовательность X1, X2,..., Xn,... (1) независимых случайных величин (См. Случайная величина) (или векторов), имеющих одно и то же (неизвестное) Распределение вероятностей с функцией распределения F (x). Часто предполагают, что функция F (x) зависит неизвестным образом от одного или нескольких параметров и определению подлежат лишь значения самих этих параметров [например, значительная часть теории, особенно в многомерном случае, развита в предположении, что неизвестное распределение является нормальным распределением (См. Нормальное распределение), у которого все параметры или какая-либо часть их неизвестны (см. Статистический анализ многомерный)]. Два основных вида С. о. — т. н. точечное оценивание и оценивание с помощью доверительных границ (См. Доверительные границы). В первом случае в качестве приближённого значения для неизвестной характеристики выбирают какую-либо одну функцию от результатов наблюдений, во втором — указывают интервал значений, с высокой вероятностью «накрывающий» неизвестное значение этой характеристики. В более общих случаях интервалы, образуемые доверительными границами (доверительные интервалы), заменяются более сложными доверительными множествами. О С. о. функции распределения F (x) см. Непараметрические методы в математической статистике; о С. о. параметров см. Статистические оценки. Разработаны также методы С. о. и для случая, когда результаты наблюдений (1) зависимы, и для случая, когда индекс n заменяется непрерывно меняющимся аргументом t, т. е. для случайных процессов (См. Случайный процесс). В частности, широко используется С. о. таких характеристик случайных процессов, как корреляционная функция и спектральная функция. В связи с задачами регрессионного анализа (См. Регрессионный анализ) был развит новый метод С. о. — Стохастическая аппроксимация. При классификации и сравнении способов С. о. исходят из ряда принципов (таких, как состоятельность, несмещенность, инвариантность и др.), которые в их наиболее общей форме рассматривают в Статистических решений теории (См. Статистических решений теория). Лит.: Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975; Рао С. Р., Линейные статистические методы и их применения, пер. с англ., М., 1968.
|



 можно описать, например, его функцией распределения
можно описать, например, его функцией распределения  , построим по выборке «оценку» для этой функции.
, построим по выборке «оценку» для этой функции.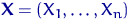 объема
объема  , называется случайная функция
, называется случайная функция  , при каждом
, при каждом  равная
равная Напоминание:Случайная функция
Напоминание:Случайная функция называется индикатором события
называется индикатором события  . При каждом
. При каждом  это — случайная величина, имеющая распределение Бернулли с параметром
это — случайная величина, имеющая распределение Бернулли с параметром  . почему?
. почему? , равное истинной вероятности случайной величине
, равное истинной вероятности случайной величине 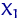 быть меньше
быть меньше  ,
,  упорядочить по возрастанию (на каждом элементарном исходе), получится новый набор случайных величин, называемый вариационным рядом:
упорядочить по возрастанию (на каждом элементарном исходе), получится новый набор случайных величин, называемый вариационным рядом: Пример 1.
Пример 1.


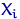 равна
равна  , где
, где  — количество элементов выборки, совпадающих с
— количество элементов выборки, совпадающих с 
 (или область выборочных данных) делят независимо от выборки на некоторое количество интервалов (не обязательно одинаковых). Пусть
(или область выборочных данных) делят независимо от выборки на некоторое количество интервалов (не обязательно одинаковых). Пусть  ,
,  — интервалы на прямой, называемые интервалами группировки. Обозначим для
— интервалы на прямой, называемые интервалами группировки. Обозначим для  через
через  число элементов выборки, попавших в интервал
число элементов выборки, попавших в интервал  :
:
 — длина интервала
— длина интервала  прямоугольника над
прямоугольника над 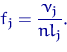

 на 4 равных отрезка. В отрезок
на 4 равных отрезка. В отрезок  попали 4 элемента выборки, в
попали 4 элемента выборки, в  — 6, в
— 6, в  — 3, и в отрезок
— 3, и в отрезок  попали 2 элемента выборки. Строим гистограмму (рис. 2). На рис. 3 — тоже гистограмма для той же выборки, но при разбиении области на 5 равных отрезков.
попали 2 элемента выборки. Строим гистограмму (рис. 2). На рис. 3 — тоже гистограмма для той же выборки, но при разбиении области на 5 равных отрезков.