 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Способы образования выборочной совокупности
Математические методы в практической деятельности. Содержание: Введение 1. Предмет математической статистики и методы 2. Основные понятия математической статистики
2.2.Способы образования выборочной совокупности Общая схема выборочного эксперимента 2.5. Эмпирическая функция распределения, гистограмма Статистическая совокупность и статистические признаки Вариационные ряды 5. Исследование разделов высшей математики, использующихся в военном деле. 6. Типичные примеры практических ситуаций деятельности военного человека, решаемых методами высшей математики Заключение Список литературы Введение Рассмотрим методы построения эмпирических распределений, т.е. распределений элементов выборки по значениям изучаемого признака. Построение эмпирических распределений — необходимый этап применения статистических методов. Выборочные данные, полученные в ходе эксперимента, называются соответственно экспериментальными (эмпирическими) данными. 1. Предмет математической статистики и методы Математическая статистика — это раздел математики, посвященный методам сбора, анализа и обработки статистических данных для научных и практических целей. Математи́ческая стати́стика — наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала (напр., оценить необходимый объём выборки для получения результатов требуемой точности при выборочном обследовании). Статистические данные представляют собой данные, полученные в результате обследования большого числа объектов или явлений (то есть, математическая статистика имеет дело с массовыми явлениями).
Математическая статистика подразделяется на две обширные области:
Методы анализа массовых явлений — предмет многих научных дисциплин; но только в том случае, когда для анализа привлекаются формальные (абстрактные) математические модели, эти методы становятся статистическими. Трудно найти современную область научных исследований, где бы ни использовались методы математической статистики. В последнее время они нашли широкое применение в медицине, биологии, социологии, т. е. в областях, сравнительно недавно считавшихся далекими от математики. Математическая статистика — раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений. В зависимости от математической природы конкретных результатов наблюдений статистика математическая делится на статистику чисел, многомерный статистический анализ, анализ функций (процессов) и временных рядов, статистику объектов нечисловой природы. Выделяют описательную статистику, теорию оценивания и теорию проверки гипотез. Описательная статистика есть совокупность эмпирических методов, используемых для визуализации и интерпретации данных (расчет выборочных характеристик, таблицы, диаграммы, графики и т. д.), как правило, не требующих предположений о вероятностной природе данных. Некоторые методы описательной статистики предполагают использование возможностей современных компьютеров. К ним относятся, в частности, кластерный анализ, нацеленный на выделение групп объектов, похожих друг на друга, и многомерное шкалирование, позволяющее наглядно представить объекты на плоскости. Методы оценивания и проверки гипотез опираются на вероятностные модели происхождения данных. Эти модели делятся на параметрические и непараметрические. В параметрических моделях предполагается, что характеристики изучаемых объектов описываются посредством распределений, зависящих от (одного или нескольких) числовых параметров. Непараметрические модели не связаны со спецификацией параметрического семейства для распределения изучаемых характеристик. В математической статистике оценивают параметры и функции от них, представляющие важные характеристики распределений (например, математическое ожидание, медиана, стандартное отклонение, квантили и др.), плотности и функции распределения и пр. Используют точечные и интервальные оценки. Большой раздел современной математической статистики — статистический последовательный анализ, фундаментальный вклад в создание и развитие которого внес А. Вальд во время Второй мировой войны. В отличие от традиционных (непоследовательных) методов статистического анализа, основанных на случайной выборке фиксированного объема, в последовательном анализе допускается формирование массива наблюдений по одному (или, более общим образом, группами), при этом решение об проведении следующего наблюдения (группы наблюдений) принимается на основе уже накопленного массива наблюдений. Ввиду этого, теория последовательного статистического анализа тесно связана с теорией оптимальной остановки. В математической статистике есть общая теория проверки гипотез и большое число методов, посвящённых проверке конкретных гипотез. Рассматривают гипотезы о значениях параметров и характеристик, о проверке однородности (то есть о совпадении характеристик или функций распределения в двух выборках), о согласии эмпирической функции распределения с заданной функцией распределения или с параметрическим семейством таких функций, о симметрии распределения и др. Большое значение имеет раздел математической статистики, связанный с проведением выборочных обследований, со свойствами различных схем организации выборок и построением адекватных методов оценивания и проверки гипотез. Задачи восстановления зависимостей активно изучаются более 200 лет, с момента разработки К. Гауссом в 1794 г. метода наименьших квадратов. Разработка методов аппроксимации данных и сокращения размерности описания была начата более 100 лет назад, когда К. Пирсон создал метод главных компонент. Позднее были разработаны факторный анализ[2] и многочисленные нелинейные обобщения. Различные методы построения (кластер-анализ), анализа и использования (дискриминантный анализ) классификаций (типологий) именуют также методами распознавания образов (с учителем и без), автоматической классификации и др. В настоящее время компьютеры играют большую роль в математической статистике. Они используются как для расчётов, так и для имитационного моделирования (в частности, в методах размножения выборок и при изучении пригодности асимптотических результатов). В своей практике естествоиспытателю приходится обрабатывать большие массивы данных, полученных в результате эксперимента путем измерений, наблюдений, анализа проб и т.п. Часто этим данным присуща изменчивость, вызванная случайными ошибками.Природа этих ошибок может быть различной: погрешность измерительных приборов,неоднородность образцов проб и др. Как правило, экспериментатор имеет возможность многократно повторить свой опыт и получить большое количество однородных данных.Затем перед исследователем встает задача обработки этих данных, чтобы извлечь как можно более точную информацию об измеряемой величине. Мы приступаем к изложению базовых принципов и методов статистической обработки данных. Задачи, решаемые математической статистикой, являются, в некотором смысле, обратными задачам теории вероятностей. Вероятностные задачи, как правило, устроены следующим образом: распределения случайных величин считаются изначально известными, основываясь на знании этих распределений требуется найти вероятности различных событий,математические ожидания, дисперсии, моменты распределений и т.п. В статистических задачах само распределение считается неизвестным, и целью исследования является получение более или менее достоверной информации об этом распределении на основе данных, собранных в результате наблюдений (экспериментов).
2. Основные понятия математической статистики
2.1 Основные понятия выборочного метода Сплошное наблюдение, т.е. изучение всех членов совокупности, сначала кажется единственно возможным способом получения о ней достаточно точной информации. На самом деле это не всегда так. Рассмотрим некоторые примеры. Пусть на заводе за день изготовляется большая партия лампочек. Не контролировать срок их службы, конечно, нельзя. Однако если это будет сделано в стенах завода в отношении каждой лампочки, то, получив полную картину о долговечности лампочек, мы их все выведем из строя и ни одна не дойдет до потребителя. С такой «проверкой», безусловно, нельзя согласиться. В аналогичных условиях находятся предприятия, производящие консервы (мясные, рыбные и др.), ткани, искусственные волокна, строительные материалы (цемент, кирпич, бетон) и т, д. Сплошное наблюдение нецелесообразно не только в случаях, когда оно приводит к уничтожению всех подлежащих рассмотрению объектов. Например, при составлении баланса денежных доходов и расходов населения нашей страны, при планировании денежного обращения, розничного товарооборота, транспортных тарифов, при проведении мероприятий по повышению материального и культурного уровня жизни народа необходимы данные о бюджетах семей трудящихся. Сбор этих данных осуществляется статистическими органами. Один работник-статистик в состоянии вести ежедневные записи доходов, расходов, потребления и т. д. не более чем в 20—25 семьях одновременно. Для обследования только бюджетов трудящихся нашей страны понадобилось бы несколько миллионов работников. Кроме того, для обработки собранных данных необходимо большое число специалистов. Выделить такое количество рабочей силы практически невозможно и нецелесообразно. Средством для получения необходимой информации в подобных случаях остается несплошное наблюдение. Широкое применение находит выборочный метод исследования. Суть этого метода: если по результатам изучения сравнительно небольшой ее части можно получить с достаточной для практики достоверностью необходимую информацию о всей совокупности, то нет необходимости в сплошном наблюдении. Часть объектов исследования, определенным образом избранная из более обширной совокупности, называется выборкой, а исходная совокупность, из которой взята выборка, — генеральной (основной) совокупностью. Вся подлежащая изучению совокупность объектов называется генеральной совокупностью. Та часть объектов, которая попала на исследование, называется выборочной совокупностью (или просто выборкой). Важнейшая характеристика выборки — объем выборки, т. е. число элементов в ней. Число элементов в генеральной совокупности называется объемом генеральной совокупности (обозначается N). Относительно N, как правило, делается предположение, что он бесконечно велик, т. е. выборка получается из бесконечной генеральной совокупности. Число элементов в выборке называется объемом выборки (обозначается n). Способы образования выборочной совокупности Чтобы иметь право судить о генеральной совокупности по выборке, последняя должна быть образована случайно. Этого можно достичь различными способами. Существуют различные виды выборок: · собственно-случайная; · механическая; · типическая; · серийная… Члены генеральной совокупности можно предварительно занумеровать, а каждый номер записать на отдельной карточке. Отбирая наудачу после тщательного перемешивания из пачки таких карточек по одной карточке, получим выборочную совокупность любого нужного объема, которая называется собственно-случайной. Номера на отобранных карточках укажут, какие члены генеральной совокупности попали в выборку. При этом возможны два принципиально различных способа огбора карточек в зависимости от того, возвращается или не возвращается обратно вынутая карточка после записи ее номера. Выборочная совокупность, образованная по первой схеме» называется собственно-случайной, а повторным отбором членов, по второй — собственно-случайной о бесповторным отбором членов. Для краткости далее их будем часто называть соответственно повторной и бесповторной выборками. Собственно-случайная бесповторная выборка образуется и в том случае, когда из тщательно перемешанной пачки сразу взято нужное число карточек. Собственно-случайную выборку заданного объема п можно образовать и с помощью так называемых таблиц случайных чисел или генератора случайных чисел на компьютере. При образовании собственно-случайной выборки каждый член генеральной совокупности с одинаковой вероятностью может попасть в выборку. Выборка, в которую члены из генеральной совокупности отбираются через определенный интервал, называется механической. Например, если объем выборки должен составлять 5% объема генеральной совокупности (5%-ная выборка), то отбирается ее каждый 20-й член, при 10%-ной выборке — каждый 10-й член генеральной совокупности и т.д. Механическую выборку можно образовать, если имеется определенный порядок следования членов генеральной совокупности, например, если они следуют друг за другом в определенной последовательности во времени. Именно так появляются готовые детали со станка, приборы с конвейера и т, п. При этом необходимо убедиться, что в следующих один за другим членах генеральной совокупности значения признака не изменяются с той же (или кратной ей) периодичностью, что и периодичность отбора элементов в выборку. Пусть из продукции станка в выборку попадает каждая пятая деталь, а после каждой десятой детали рабочий производит смену (или заточку) режущего инструмента и подналадку станка. Эти операции рабочего направлены на улучшение качества деталей, износ режущего инструмента происходит более или менее равномерно. Следовательно, в выборочную совокупность попадут детали, на качество которых работа станка влияет в одну и ту же сторону, а показатели выборочной совокупности могут неправильно отразить соответствующие показатели генеральной совокупности. Если из предварительно разбитой на непересекающиеся группы генеральной совокупности образовать собственно-случайные выборки из каждой группы (с повторным или бесповторным отбором членов), то отобранные элементы составят выборочную совокупность, которая называется типической. Оказывается, что выборочная совокупность с большей достоверностью воспроизводит однородную генеральную совокупность. Качество изделий различных цехов, участков, станков и смен может оказаться существенно различным. Поэтому при изучении качества изделии, выпускаемых предприятием, целесообразно образовывать выборку не из общей массы изготовляемой предприятием продукции, а из продукции отдельно каждого цеха. смены (ночной, дневной) и даже участка, станка, т. е. образовать типическую выборку. Если генеральную совокупность предварительно разбить на непересекающиеся серии (группы), а затем, рассматривая серии как элементы, образовать собственно-случайную выборку (с повторным или бесповторным отбором серий), то все члены отобранных серий составят выборочную совокупность, которая называется серийной. Пример 1 Предположим, что на заводе 150 станков (10 цехов по 15 станков) производят одинаковые изделия. Если в выборку отбирать изделия из тщательно перемешанной продукции всех 150 станков, то образуется собственно-случайная выборка. Но можно отбирать изделия отдельно из продукции первого, второго и т. д. станков. Тогда будет образована типическая выборка. Если же членами генеральной совокупности считать цехи и в каждом из цехов образовать повторную или бесповторную выборку, то вся отобранная продукция составит серийную выборку. Пример 2
Пусть Будем считать, что, проведя Рассмотрим подробнее набор В серии уже произведенных экспериментов выборка — это набор чисел. Но если эту серию экспериментов повторить еще раз, то вместо этого набора мы получим новый набор чисел. Вместо числа Выборка Что значит «по выборке сделать вывод о распределении»? Распределение характеризуется функцией распределения, плотностью или таблицей, набором числовых характеристик — 2.3 Выборочное распределение
Распределение величины
В общем случае обозначим через
|



 — случайная величина, наблюдаемая в случайном эксперименте. Предполагается, что вероятностное пространство задано (и не будет нас интересовать).
— случайная величина, наблюдаемая в случайном эксперименте. Предполагается, что вероятностное пространство задано (и не будет нас интересовать). раз этот эксперимент в одинаковых условиях, мы получили числа
раз этот эксперимент в одинаковых условиях, мы получили числа 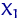 ,
,  ,
,  ,
,  — значения этой случайной величины в первом, втором, и т.д. экспериментах. Случайная величина
— значения этой случайной величины в первом, втором, и т.д. экспериментах. Случайная величина  имеет некоторое распределение
имеет некоторое распределение  , которое нам частично или полностью неизвестно.
, которое нам частично или полностью неизвестно.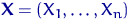 , называемый выборкой.
, называемый выборкой. , и т.д.) — переменная величина, которая может принимать те же значения, что и случайная величина
, и т.д.) — переменная величина, которая может принимать те же значения, что и случайная величина  ,
,  ,
,  и т.д. По выборке нужно уметь строить приближения для всех этих характеристик.
и т.д. По выборке нужно уметь строить приближения для всех этих характеристик. — набор чисел
— набор чисел  ,
,  . На подходящем вероятностном пространстве введем случайную величину
. На подходящем вероятностном пространстве введем случайную величину  , принимающую значения
, принимающую значения  (если какие-то из значений совпали, сложим вероятности соответствующее число раз). Таблица распределения вероятностей и функция распределения случайной величины
(если какие-то из значений совпали, сложим вероятности соответствующее число раз). Таблица распределения вероятностей и функция распределения случайной величины 


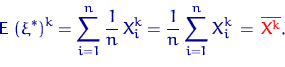
 величину
величину
 ,
,  ,
,  ,
,  ,
,  — станут величинами случайными. Эти характеристики выборочного распределения используют для оценки (приближения) соответствующих неизвестных характеристик истинного распределения.
— станут величинами случайными. Эти характеристики выборочного распределения используют для оценки (приближения) соответствующих неизвестных характеристик истинного распределения. — количество очков, выпавших при
— количество очков, выпавших при  -м броске,
-м броске,  . Предположим, что единица в выборке встретится
. Предположим, что единица в выборке встретится  раз, двойка —
раз, двойка —  раз и т.д. Тогда случайная величина
раз и т.д. Тогда случайная величина  ,
,  соответственно. Но эти пропорции с ростом
соответственно. Но эти пропорции с ростом  согласно закону больших чисел. То есть распределение величины
согласно закону больших чисел. То есть распределение величины