ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Критерий Стьюдента (t-критерий)
Критерий позволяет найти вероятность того, что оба средних значения в выборке относятся к одной и той же совокупности. Данный критерий наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности». При использовании критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и экспериментальная (опытная) группа, количество испытуемых в группах может быть различно. Во втором случае, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными. А) случай независимых выборок Статистика критерия для случая несвязанных, независимых выборок равна:
где
где n1 и n2 соответственно величины первой и второй выборки. Если n1=n2, то стандартная ошибка разности средних арифметических будет считаться по формуле:
где n величина выборки. Подсчет числа степеней свободы осуществляется по формуле: k = n1 + n2 – 2. (4) При численном равенстве выборок k = 2n - 2. Далее необходимо сравнить полученное значение tэмп с теоретическим значением t—распределения Стьюдента (см. приложение к учебникам статистики). Если tэмп<tкрит, то гипотеза H0 принимается, в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза. Б) случай связанных (парных) выборок В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента. Вычисление значения t осуществляется по формуле:
где Sd вычисляется по следующей формуле:
Число степеней свободы k определяется по формуле k=n-1. Рассмотрим пример использования t-критерия Стьюдента для связных и, очевидно, равных по численности выборок. Если tэмп<tкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная. F — критерий Фишера Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фишера такова:
где Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значение Fэмп всегда будет больше или равно единице. Число степеней свободы определяется также просто: k1=nl - 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k2=n2 - 1 для второй выборки. В Приложении 1 критические значения критерия Фишера находятся по величинам k1 (верхняя строчка таблицы) и k2 (левый столбец таблицы). Если tэмп>tкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная. 33.Дисперсионный анализ. В дисперсионном анализе устанавливается факт зависимости или не зависимости исследуемой случайной величины от одного или нескольких факторов. Анализ проводится по каждому фактору отдельно или по нескольким факторам одновременно, т.е. мы можем выделить: -однофакторный -двухфакторный -трехфакторный Однофакторный дисперсионный анализ. Пусть проверяется гипотеза
Для проверки вычисляются оценки мат. ожиданий на всех уровнях Зависимость исследуемой величины можно обнаружить при сравнении оценок Опуская коэффициент Идея дисперсионного анализа состоит в том, что эта сумма разбиваются на 2 компоненты, одна из них обусловлена фактором влияния А, а другая другими неучтенными факторами. Проведем это разбиение. Q= т.к. Обозначим первое слaгаемое
Для сравнения необходимо использовать признаки (критерии). По условию величина Х имеет нормальное распределение и т.к. Q= k(n-1), тогда по критерию Фишера , где F-распределение Фишера со степенями свободы
Из этого же уравнения находится критическое значение Если отношение F оказывается большим, то влияние фактора А следует признать существенным. Замечание: для вычислений Q удобно пользоваться формулами:
34.Дисперсионный анализ. В дисперсионном анализе устанавливается факт зависимости или не зависимости исследуемой случайной величины от одного или нескольких факторов. Анализ проводится по каждому фактору отдельно или по нескольким факторам одновременно, т.е. мы можем выделить: -однофакторный -двухфакторный -трехфакторный Двухфакторный дисперсионный анализ. Проводится аналогично однофакторному. По каждому фактору вычисляется свое отношение F, находится критическое Пусть проверяется влияние на величину х факторов А и В. Предположим, что фактор А имеет к-уровней, фактор В n-уровней. Измерение величины х на i-ом уровне фактора А и j-ом уровне фактора В обозначим Мат. ожидания:
Пусть эмпирическим мат. ожиданиям соответствуют истинные ожидания величин
Для проверки гипотезы суммируют квадраты отклонения общего мат. ожидания и эмпирических измерений. Сумма разбивается на 3 компоненты Q= Общая сумма:
Т.к. по условия величина Х имеет нормальное распределение с дисперсией Все мат. ожидания также будут распределены по нормальному закону:
Предположим, что гипотеза Тогда отношение F определяются по формулам:
Задаем уровень значимости α и по таблице распределения Фишера находим критические значения Если Для вычисления Q удобней воспользоваться формулами:
35.С ростом числа факторов увеличивается число измерений и соответственно число вычислительных операций. Для упрощения проверки используют альтернативные схемы проведения эксперимента. Например в трех факторном анализе популярен латинский квадрат. Пусть СВ Х зависит от трех факторов А, В, С. Каждый фактор имеет n уровней, тогда количество измерений при полном исследовании будет Измеряемые значения х индексируют по факторам А и В.
и вычисляют отдельно для каждого уровня фактора С. Эмпирическое мат. ожидание вычисляют по формулам:
Далее процедура анализа как и ранее. Выделяем Q=
Число степеней свободы одинаково для всех (n-1) и (n-1)(n-2). Решение о гипотезе принимается аналагично по сравнению с критическими значениями Рассмотрим общую схему трехфакторного анализа: Предположим, что на СВ х влияют 3 фактора: А,В,С. Требуется определить степень влияния факторов на х, т.е. существенно или нет это влияние. Для этого факторы квантуются (разбиваются на уровни) Делаются измерения величины Х при разных значениях факторов. Схема выбора комбинаций уровней факторов называют планом эксперимента. Предположим, что каждый фактор имеет S- уровней, тогда число различных комбинаций - Получаем большой объем статистических измерений. Для уменьшения числа измерений используют др. планы, например латинский квадрат.В этом случае выбирают только те измерения, когда комбинации не повторяются дважды и число измерений становится равной Обозначим измерение
Проверим гипотезу Н0 о том , что все мат ожид одинаковы, т.е. Эта гипотеза эквивалентна предположению, что ни один из факторов не влияет на величину Х. Альтернативная гипотеза Н1 предполагает, что хотя бы 1 из факторов влияет на величину х, т.е. принимая Н0 мы отвергаем влияние всех факторов , принимая Н1, мы предполагаем , что хотя бы 1 фактор влияет на х, а для выявления степени влияния проводим дополнительные исследования. 36.Регрессионный анализ принимается аппроксимацией статистических данных некоторой функции, т.е. заменой статистических связей функциональной зависимостью. Решаются 2 задачи: выявление переменных фактов , влияющих на исследуемую СВ и оценка точности аппроксимации. Задача РА ставится так: пусть на СВ Z влияют факторы Х, У,…., Т Возможно влияние и других факторов , но если они не являются контролируемыми , то их можно не учитывать. Предположим, что для всех возможных величин указанных факторов выполняется соотношение: z = 𝜑( x,y,..t)+ℰ , где 𝜑( x,y,..t) – неизвестная функция ; ℰ - компонента учитывающая влияние некоторых факторов. Считаем, что ℰ не зависит от Х, У,…., Т Предположим, что ℰ имеет норм. распределение. и ее мат ожидание равно 0, а дисперсия Основная цель РА –определение вида функции 𝜑. 𝜑 называют аппроксимирующей или прогнозирующей функцией. Задача анализа разбивается на 2 этапа: 1. Определение структуры аппроксимирующей функции с точностью до неизвестных параметров. В частности вид функции одной переменной можно определить графически. 2. Определение коэффициентов аппроксимирующей функции из условий минимизации средней квадратической ошибки отклонений. Пусть проведено n измерений факторов
тогда для любой строки i мы можем составить соотношение: Средний квадрат ошибки аппроксимации: 1/n Коэффициент1/n не влияет на исследование функции S. Найдем коэффициенты функции a, b,…,h из условия минимизации.
Получаем :
Точность аппроксимации определяется дисперсией:
Для оценки степени влияния остаточной дисперсии вводим коэффициент:
А если еще зависимость линейная, то Одномерный РА Рассмотрим линейный вариант, т.е. аппроксимирующая функция будет: Z =
Получаем систему:
Для расчета мы можем использовать формулы из ТВ:
На практике коэффициент ковариации считают: Если известно, что X и Z имеют норм. распределение, то полученная аппроксимирующая функция точно совпадает с регрессией. Это связано с тем, что норм. распределение СВ могут зависеть др от др только линейно. А т.к. в реальном мире согласно центральной предельной теореме большинство СВ распределено норм., то линейные связи между переменными имеют большое значение. Всвязи с погрешностями исх. данных и влияния неучтенных факторов , коэффициент а с некоторой достоверностью мы можем определить как значение внутри интервала. Доверительный интервал для а:
37.Пусть СВ Z зависит от нескольких параметров Z = b + Предположим, что в эксперименте проведена серия из n- испытаний и b = Подставим в выражение b : Находим частные производные выражения по
………. Получим систему из k уравнений с k неизвестными. Решая систему получим:
Оценим остаточную дисперсию: Для упрощения структуры аппроксимации проведем анализ влияния переменных др на др. Строим корреляционную матрицу:
Коэффициент корреляции: 38. Нелинейный регрессионный анализ. В этом случае определяющая функция имеет не линейную структуру. Если нет особых требований, то чаще всего это полином второй и третьей степени. Для полинома второй степени
Корреляционное отношение оцениваются как:
Если структура аппроксимирующей функции Y=а𝜑(х)+b ,( где 𝜑(х) - элементарная функция), то для оценки коэффициентов сводим ее к линейной путем замены z= 𝜑 (x) Получаем Y=az+b
В общем случае не линейная регрессия сводится к минимуму путем логарифмирования выражения. 39.При исследовании случайных явлений некоторые из них меняются во времени. Например, длина очереди, рейтинг политической партии, курс доллара. СВ, меняющаяся во времени называют случайными функциями(СФ). СФ изучает теорема случайных процессов(ТСП). Методы ТСП используются в теории автоматического управления , анализе и планировании финансовой деятельности. Если каждому значению t Если зафиксировать время t , тогда СВ Х будет принимать случайные значения на некотором множестве элементарных событий Ω , т.е. случайный процесс описывается как Х (t,ω) , где t ω 1. Дискретный процесс с дискретным временем 2. Дискретный процесс с непрерывным временем 3. Непрерывный процесс с дискретным временем 4. Непрерывный процесс с непрерывным временем В 1 и 3 случае множество t принимает конкретное значение Т = {t1,t2,….tn}. В 1 случае множество значений СФ дискретно, т.е. задается дискретным распределением, во 2 случае Х(t) задается непрерывным распределением, во 2 и 4 случае множество t непрерывно, а множество состояния различно. Основные характеристики случайных процессов: 1. Мат. ожиданием случайных процессов Х(t) называется не СФ Возможные обозначения Свойства мат. ожидания: · Мат. ожид. неслучайной функции равно самой функции М(f(t)) = f(t) · Неслучайный множитель можно вынести за знак мат. ожид. М(f(t)* х(t)) = f(t) * · Мат. ожидание разности/суммы случайных процессов равно разности/сумме мат. ожиданий. М(х(t) 2. Дисперсией случайного процесса называется неслучайная функция , которая при каждом значении t равна дисперсии соответствующего сечения. Свойства дисперсии: · Дисперсия неслучайной функции равна 0 Д(f(t)) = 0 · Дисперсия случайных процессов неотрицательна. . · Дисперсия произведения неслучайной функции на случайный процесс равна произведению квадрата неслучайной функции на дисперсию процесса. 3. Среднее квадратическое отклонение. 4. Корреляционная функция случайного процесса. Для анализа связей между случайными процессами используют корреляционную функцию (аналог ковариации) Автокорреляционной функцией случ. процесса называется неслучайная функция 2- ух аргументов
Свойства автокорреляционной: · Функция при одинаковых значениях элементов равна дисперсии. · Коммутативность. · Если к случайному процессу прибавить неслучайную функцию , то ковариационная функция не изменится. · Если случайный процесс умножить на неслучайную функцию, то ковариационная функция умножится на произведение значений неслучайной функции от фиксированного времени.
· Модуль автокорреляционной функции не превышает произведения средних квадратических отклонений. ⃓ Замечание: Иногда вместо функции
Для определения степени зависимости 2-ух процессов используют взаимную корреляционную функцию.
По аналогии с автокорреляционной функцией получаем нормированную функцию. Наиболее изучаемым классом случайных процессов является стационарным. Случайный процесс Х(t) называется стационарным, если его мат. ожидание 40.Рассмотрим некоторую системуS, которая проходит случайный процесс , т.е. с течением времени система переходит из одного состояния в др. Если число состояний конечно, то процесс называют случайным с дискретными состояниями. Если переходы возможны в любой момент времени, то процесс относится к непрерывным. Случайный процесс с дискретными состояниями называют Марковским, если для любого момента времени вероятность перехода из одного состояния в другое зависит только от предыдущего состояния и не зависит от того, каким образом система попала в предыдущее состояние. Такие процессы называются процессы беспоследействия. Будущее здесь зависит только от настоящего , но не от прошлого. С помощью Марковских процессов моделируют рост популяций, организация и обслуживание очередей в теории массового обслуживания. Случайные процессы дискретными состояниями удобно отображать с помощью графических состояний. В нем возможные состояния обозначаются S возможные переходы стрелками, т.е.
Для описания марковского процесса используют вероятности состояния. Очевидно, что для любых вероятностей t сумма состояний должна быть равно единице, т.е. Предположим, что время t меняется дискретно, т.е. переход S из одного состояния в другое проходит только в моменты времени Тогда процесс можно рассматривать как последовательность или цепь событий S(0) ; S(1), где S(0) – шаг состояния системы. S(1) – состояние после 1- го шага и т.д. Такой процесс с дискретным временем и дискретным состоянием называют марковским процессом. Вероятность состояния этого процесса рассматривается как вероятность того, что на каждом шаге система находится на
Вероятностью переходов Цепи маркова называются однородной , если вероятности переходов
Р = Для однородной цепи справедлива формула : Р(n) =
|



 (1)
(1) ,
,  — средние арифметические в экспериментальной и контрольной группах,
— средние арифметические в экспериментальной и контрольной группах, - стандартная ошибка разности средних арифметических. Находится из формулы:
- стандартная ошибка разности средних арифметических. Находится из формулы: , (2)
, (2) (3)
(3) (5)
(5) — разности между соответствующими значениями переменной X и переменной У, а d - среднее этих разностей;
— разности между соответствующими значениями переменной X и переменной У, а d - среднее этих разностей; (6)
(6) (8)
(8) - дисперсии первой и второй выборки соответственно.
- дисперсии первой и второй выборки соответственно. о том, что фактор А не влияет на случайную величину Х, предполагаем, что А имеет к-уровней. На каждом уровне проводим n-измерений, получаем совокупность измерений
о том, что фактор А не влияет на случайную величину Х, предполагаем, что А имеет к-уровней. На каждом уровне проводим n-измерений, получаем совокупность измерений  i=1…k, j=1…n. Обозначим
i=1…k, j=1…n. Обозначим  - мат. ожидание на i-ом уровне фактора А. Общее мат. ожидание на всех уровнях фактора А обозначим через m. На основе экспериментальных данных требуется проверить гипотезу о равенствах мат. ожиданиях
- мат. ожидание на i-ом уровне фактора А. Общее мат. ожидание на всех уровнях фактора А обозначим через m. На основе экспериментальных данных требуется проверить гипотезу о равенствах мат. ожиданиях .
. и оценка общего мат. ожидания m:
и оценка общего мат. ожидания m: 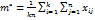 .
. с
с  , но сравнение делается не напрямую, а с помощью эмпирических дисперсий, поэтому и называется дисперсионный анализ.
, но сравнение делается не напрямую, а с помощью эмпирических дисперсий, поэтому и называется дисперсионный анализ. , рассмотрим сумму квадратов отклонений измеряемой СВ от ее мат. ожидания. kn
, рассмотрим сумму квадратов отклонений измеряемой СВ от ее мат. ожидания. kn 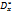 =kn*
=kn*  =Q=
=Q= 
 =
=  =
= 
 не зависимые измерения, то второе слагаемое равно 0.
не зависимые измерения, то второе слагаемое равно 0. , а второе
, а второе 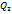 компонента
компонента  отклонение значение Х от средних значений
отклонение значение Х от средних значений  .
. и
и  будет иметь распределение
будет иметь распределение  с (nk-1) степенью свободы, аналогично величина
с (nk-1) степенью свободы, аналогично величина  . Предположим, что гипотеза
. Предположим, что гипотеза  будет распределена по закону
будет распределена по закону  , то по свойству распределений
, то по свойству распределений 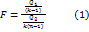
 =к-1
=к-1 =к(n-1) Затем для проверки задается уровень значимости α или вероятность ошибки 1 рода и по таблице распределения Фишера решается уравнение
=к(n-1) Затем для проверки задается уровень значимости α или вероятность ошибки 1 рода и по таблице распределения Фишера решается уравнение
 , которое является нижней границей в области F , решение по гипотезе
, которое является нижней границей в области F , решение по гипотезе  .
.

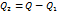



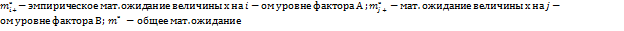
 ,
,  , m, тогда основная гипотеза
, m, тогда основная гипотеза  =
=  .
.



 характеризует влияние фактора А на величину Х и называется рассеиванием по фактору А
характеризует влияние фактора А на величину Х и называется рассеиванием по фактору А описывает влияние фактора В на величину Х и называется рассеиванием по фактору В
описывает влияние фактора В на величину Х и называется рассеиванием по фактору В указывает на рассеивание СВ внутри комбинации факторов и называется остаточное рассеивание.
указывает на рассеивание СВ внутри комбинации факторов и называется остаточное рассеивание. , то величина
, то величина  будет иметь распределение
будет иметь распределение  (nk-1)-степенью свободы.
(nk-1)-степенью свободы.

 с (к-1) степенями свободы, величина
с (к-1) степенями свободы, величина  распределена по закону
распределена по закону  распределена по закону
распределена по закону 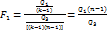

 со степенью свобод (к-1) и (к-1)(n-1) и
со степенью свобод (к-1) и (к-1)(n-1) и  со степенями свободы (n-1) и (к-1)(n-1).
со степенями свободы (n-1) и (к-1)(n-1). , то гипотеза
, то гипотеза 
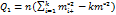


 . Идея латинского квадрата в том, что выбираем измерения, в котором каждая пара уравнений встречается только 1 раз.
. Идея латинского квадрата в том, что выбираем измерения, в котором каждая пара уравнений встречается только 1 раз.
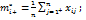
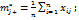

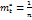
 - t – уровней фактора С
- t – уровней фактора С
 - по С ;
- по С ; 









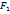 =
= 
 =
= 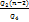
 =
= 
 .
. .
. , в дисперсионном анализе предполагается, что все измерения независимы и распределены по нормальному закону с одной и той же дисперсией
, в дисперсионном анализе предполагается, что все измерения независимы и распределены по нормальному закону с одной и той же дисперсией  +
+  , где
, где 
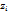 =𝜑 (
=𝜑 (  ,
, 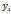 , ….,
, ….,  , a, b,…., h) +
, a, b,…., h) +  , где (
, где (  = 1/n
= 1/n  = 1/n * S
= 1/n * S = -2
= -2  *
*  = 0
= 0 = -2
= -2  = 0
= 0 = -2
= -2  = 0
= 0 ,
,  ,….,
,…., 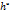
 =
=  (x, y,…, t,
(x, y,…, t,  ,
,  =
=  +
+  ,
, 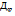 будет равна 0
будет равна 0 =
=  , где к- число параметров,
, где к- число параметров,  - статистические данные,
- статистические данные,  - расчетные данные.
- расчетные данные. =
=  = 1-
= 1- 


 + b , тогда функция S =
+ b , тогда функция S = 
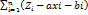 *
*  = -2
= -2 

 =
= 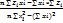
 = 1/n (
= 1/n (  –
–  )
)
 =
= 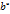
 - a
- a  , где
, где  -
-  *
* 
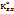 -эмпирический ковареационный момент
-эмпирический ковареационный момент
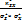
 - эмпирические стандарт. средние квадратич. отклонения
- эмпирические стандарт. средние квадратич. отклонения -(1/n
-(1/n  ) (1/n *
) (1/n * 
 *
*  < a <
< a <  находится как Ф(
находится как Ф( 
 Нужно оценить коэффициенты b и
Нужно оценить коэффициенты b и  . i = 1….. k
. i = 1….. k - номер серии. Коэффициенты b и
- номер серии. Коэффициенты b и  min (b и
min (b и  , где
, где 
 = 1/n
= 1/n  эмпирические мат. ожидания
эмпирические мат. ожидания → min
→ min
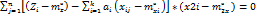
 ,
,  , …. ,
, …. ,  и аппроксимирующая функция :
и аппроксимирующая функция : (
( 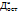 =
=  , где n – число измерений, k – число переменных.
, где n – число измерений, k – число переменных.
 Если найдутся переменные, для которых ⃓
Если найдутся переменные, для которых ⃓  ⃓= 1 то одну из них можно опустить. Если для некоторых переменных
⃓= 1 то одну из них можно опустить. Если для некоторых переменных 
 0, то эту переменную можно не учитывать.
0, то эту переменную можно не учитывать. коэффициенты определяются из системы:
коэффициенты определяются из системы:


 Т поставлена в соответствие СВ Х(t) , то говорят , что на множестве Т задана СФ. Чаще всего Т – интервал времени. И если t – время, то Х(t) – случайный процесс. Случайный процесс может быть задан аналитически, с помощью распределения ,графически.
Т поставлена в соответствие СВ Х(t) , то говорят , что на множестве Т задана СФ. Чаще всего Т – интервал времени. И если t – время, то Х(t) – случайный процесс. Случайный процесс может быть задан аналитически, с помощью распределения ,графически. Т ( временной интервал) ,
Т ( временной интервал) , Ω (пространство элементарных событий). При фиксированном t получаем СВ: Х(
Ω (пространство элементарных событий). При фиксированном t получаем СВ: Х(  ; ω), называемую сечением процесса : Х(
; ω), называемую сечением процесса : Х(  ;
;  ) Реализация случайного процесса зависит от времени. Случайный процесс представляет собой переходы системы из одного состояния в др случайным образом. В зависимости от множества состояния случайные процессы делят на классы:
) Реализация случайного процесса зависит от времени. Случайный процесс представляет собой переходы системы из одного состояния в др случайным образом. В зависимости от множества состояния случайные процессы делят на классы: (t) , которая при любом фиксированном значении аргумента t равно мат. ожид. сечения случайного процесса.
(t) , которая при любом фиксированном значении аргумента t равно мат. ожид. сечения случайного процесса.  (Т)
(Т)
 у(t)) =
у(t)) = 
 (t) Функция
(t) Функция  = ДХ(t) = M
= ДХ(t) = M  (t) –
(t) –  (t) Дисперсия характеризует рассеяние случайных процессов.
(t) Дисперсия характеризует рассеяние случайных процессов. (t)
(t) 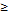 0
0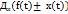 =
=  (t) =
(t) = 
 = М((х –
= М((х –  (t1,t2) , которая при каждой паре значений равна ковариации значений х(t1), х(t2).
(t1,t2) , которая при каждой паре значений равна ковариации значений х(t1), х(t2).

 ⃓
⃓ 
 (t2)
(t2) =
= 
 = М ((X(t1) –
= М ((X(t1) –  (t2))), где X(t) и Y(t) – называется некоррелированным, если их
(t2))), где X(t) и Y(t) – называется некоррелированным, если их 
 =
= 
 =
=  . Большинство стационарных процессов обладают эргодическим свойством. Его смысл: По одной достаточно длинной реализации можно судить о свойствах всего процесса , т.е. характеристики случайного процесса
. Большинство стационарных процессов обладают эргодическим свойством. Его смысл: По одной достаточно длинной реализации можно судить о свойствах всего процесса , т.е. характеристики случайного процесса  и
и 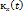 определяются как среднее по одной реализации. Достаточным условием эргодичности процесса является стремление к 0 корреляционной функции.
определяются как среднее по одной реализации. Достаточным условием эргодичности процесса является стремление к 0 корреляционной функции. 
 →
→  →…..
→….. (t),
(t),  (t), ….. – вероятность того, что в момент времени t система находится в соответствующем состоянии .
(t), ….. – вероятность того, что в момент времени t система находится в соответствующем состоянии .  = 1
= 1

 …….., где
…….., где  -
-  –
– 
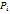 (k) = P{S(k) =
(k) = P{S(k) =  ) надо знать первоначальное распределение вероятностей
) надо знать первоначальное распределение вероятностей 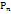 (0), т.е. вероятности состояния в начальный момент времени и вероятности переходов
(0), т.е. вероятности состояния в начальный момент времени и вероятности переходов  (k)
(k) .
. Элементы матрицы обладают свойствами:
Элементы матрицы обладают свойствами: 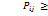 0
0 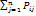 = 1
= 1