 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Теорема Чебышева(основное утверждение ЗБЧ)
В ней используется понятие сходимости по вероятности. При достаточно большом числе независимых испытаний
Переходя в фигурных скобках к противоположному событию, получаем
Теорема Чебышева позволяет с достаточной точностью по средней арифметической судить о математическом ожидании или, наоборот, по математическому ожиданию предсказывать ожидаемую величину средней. Так, на основании этой теоремы можно утверждать, что если проведено достаточно большое количество измерений определённого параметра прибором, свободным от систематической погрешности, то средняя арифметическая результатов этих измерений сколь угодно мало отличается от истинного значения измеряемого параметра. Теорема Бернулли Теорема Бернулли устанавливает связь между относительной частотой появления события и его вероятностью. Если в каждом из
При доказательстве теоремы Бернулли получаем оценку
Как видим, теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности Теорема 1(неравенство Маркова). Если случайная величина Центральная предельная теорема устанавливает условия, при которых закон распределения случайной величины неограниченно приближается к нормальному. Теорема Ляпунова объясняет широкое распространение нормального закона распределения и поясняет механизм его образования. Теорема позволяет утверждать, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин, дисперсии которых малы по сравнению с дисперсией суммы, закон распределения этой случайной величины оказывается практически нормальным законом. А поскольку случайные величины всегда порождаются бесконечным количеством причин и чаще всего ни одна из них не имеет дисперсии, сравнимой с дисперсией самой случайной величины, то большинство встречающихся в практике случайных величин подчинено нормальному закону распределения
21. МС занимается анализом, сбором , систематизацией и обработкой статистической информации, полученной в результате наблюдений массовых случайных явлений. Она предполагает выявление закономерностей между случ. данными , используя методы ТВ. В отличие от ТВ МС оперирует реальными данными. Предметом МС можно назвать изучение СВ по результатам наблюдения. Полученные в наблюдениях данные упорядочивают и проводят их оценку с к-л теоретическим распределением, оценивают их мат. ожидание и дисперсию. Еще одной задачей МС является проверка статистических гипотез . Здесь выдвигают гипотезу о том, что данные удовлетворяют известному распределению, чаще всего нормальному, и проверяют гипотезу с помощью различных критериев. Третьей задачей МС можно назвать определение взаимозависимости между результатами наблюдения. МС начинается с 18в. Наиболее известные ученые в области МС: Бернулли, Пирсон, Фишер, Чебышев, Колмогоров, Ляпунов. 22. Пусть требуется изучить совокупность объектов по некоторому признаку. Совокупность всех изучаемых объектов называют генеральной, т.е. генеральная совокупность- множество всех Х, заданных на постоянстве элементарных событий Ω Не всегда возможно исследовать все объекты, поэтому делают выборку. Выборочная совокупность-множество объектов отобранных из генеральной совокупности случайным образом. Если объектов n, то n – объем выборки. Метод статистического исследования, состоящий в том, что на основе выборочной совокупности делается вывод о свойствах всей генеральной совокупности, называется выборочным. Для того, чтобы оценка совокупности была объективной , необходимо, чтобы выборка была репрезентативной ( представительной) Различают выборки с возвращением, т.е. объек после исследования возвращают в группу. По методам отбора выбирают простые выборки, т.е. выбирают по одному предмету без всяких условий. Типические выборки,т.е. совокупность делят на группы и выбирают одного представителя группы. Механические – выбирают объекты через определенный интервал. Серийные – выбирают сразу серию объектов. Возможны сочетания вариантов выбора. Пусть изучается некоторая СВ Х, на основе наблюдений или опытов получаем, что некий признак Х принял значение Х1 n1 раз, Х2 n2 раз и т.д. Хк nк раз. Х1,Х2….Хк – варианты n1,n2….nк – частоты n1+n2+…+nк =n – объем выборки ni/n – относительные частоты Перечень всех вариант называют вариационным рядом. После наблюдений варианты ранжируют по возрастанию Х1<Х2<Х3<….. Запись вариант вместе с их частотами называют статистическим распределением выборки.
Статистическое распределение является оценкой неизвестного теоретического распределения Если число вариант велико, то переходят к интервальному ряду (Х0;Х1)(Х1;Х2)…… h(шаг распределения)= Х1-Х0=Х2-Х1=…… он обычно постоянен. Для определения h используется формула Стерджеса : h=(Хмах - Хмин)/(1+ log2(n)) Хмах- Хмин = R размах выборки Хнач = Хмин- h/2 Число интервалов m = 1+ log2(n) = 1+ lg(n) Функция Fn(x) является оценкой теоретиеской функции распределения, т.е. для любого 23.Графически статистическое распределение изображают с помощью полигона и гистограммы.
Площадь гистограммы равна объему выборки 24. 1) Выборочное среднее В случае интервального ряда в качестве хi будут средние значения интервалов. 2) Выборочная дисперсия (Дв) Дв = 1/n Среднее арифметическое квадратов отклонения выборки от выборочного среднего Дв = 1/n Дв = 3) Выборочное среднее квадратическое отклонение σ = На практике чаще используют исправленную дисперсию
S – среднее исправленное квадратичное отклонение В качестве R- размах вариант вариационного ряда используют моду Медиана n= 2k следовательно 25.Пусть изучается случайная величина Х с законом распределения зависимости от нескольких параметров (а, σ). Требуется по выборке Статистической оценкой -несмещенность –Оценка -состоятельность -оценка называется состоятельной, если она сходиться по вероятности к оцениваемому параметру, т.е. При увлечении числа измерений n статистическая оценка -эффективность – состоятельная оценка На практике все 3 оценки для 1 параметра встречается крайне редко. В этом случае Точечные оценки мат. ожидания и дисперсии: Пусть изучается СВ Х с мат. ожиданием М(Х) и дисперсией Д(Х). Оба параметра неизвестны. Статистика, используемая в качестве приближенного значения неизвестного параметра, называется точечной. Получаем , что точечная оценка – одно число, рассчитываемое по выборке Пусть
При нормальном распределении она будет и эффективной. Мат. ожидание выборочной дисперсии: 1. М( 2.
3. Относительная частота наступления события А в n испытаниях. 4. 26.Метод моментов состоит в приравнивании теоретических моментов распределения соответствующим эмпирическим моментов найденных по выборке. μ-начальный момент ν-центральный момент Если распределение зависит от одного параметра ϴ, то для его оценки надо решить 1 уравнение М(х)= Распределение зависит от двух параметров Если параметров к
Метод был предложен Пирсонам в 1894 году Оценки метода: состоятельные, но их эффективность <1 27.Предложил Фишер Для некоторой выборки
где f(х, ϴ)-закон распределения
П-произведение Если распределение дискретное, то плотность вероятности f заменяется на вероятность р
Чем больше значение функции L, тем более правдоподобнее распределение
Находим
28.Интервальной называют оценку , которая определяется двумя числами – концами интервала, показывающего оцениваемый параметр. Точечные оценки параметра Задача интервального оценивания состоит в построении числового интервала, относительно которого можно сказать, что внутри него с заданной вероятностью γ находится точное значение оцениваемого параметра , такой интервал называют доверительным. Доверительным называют интервал, который с заданной надежностью γ показывает заданный параметр. Вероятность γ называют надежностью оценки. Доверительный интервал часто строят симметрично относительно оценки Доверительные интервалы для нормального распределения: 1. Доверительный интервал для мат. ожидания при известной дисперсии. СВ Х распределена по норм. закону с параметрами а и σ . σ известна , надежность γ будем считать заданной. Делаем выборку из n наблюдений. Д( Оценка мат. ожид. распределена по закону нормальному с параметрами а; γ = Р(⃓ Тогда надежность γ получается как: γ = Р{⃓ Вероятность того, что а : Р{⃓ Для вычисления доверительного интервала получаем: Из табл. функции Лапласа находим t и определяем интервал. 2. Для оценки мат. ожид. и неизвестной дисперсии СВ Х распределена нормально с параметрами а и σ. Нужно с надежностью γ определить интервал γ = Р(⃓ S = Величина 3. Интервал для среднего квадратичного отклонения при неизвестной дисперсии. Пусть СВ Х распределена по норм. закону с параметрами а и σ. σ неизвестна, тогда интервал оценки σ (
Существует еще один вариант оценки σ : S (1- q) < σ < S (1+ q) , q берется из табл. для известных n и γ 4. Доверительный интервал для вероятности биномиального распределения при больших n . P → ( 29. 30.Одной из основных задач статистики является выдвижение предложений о статистическом распределении и обосновании этого предложения. Статистическим методом гипотезу можно только принять или опровергнуть, но нельзя доказать. Под статистической гипотезой понимают предположение о генеральной совокупности сделанное по выборке. Эти гипотезы делятся: о предмете распределения и о виде распределения. Одну из гипотез выбирают как основную (Н0), противоположную ей гипотезу считают конкурирующей и обозначают Н1 Гипотезы могут быть сложными и простыми. Гипотеза о том, что М(Х)= Q0 считается простой гипотезой. Конкурирующая гипотеза Н1: М(Х) ≠ Q0 считается сложной, т.к. она состоит из 2 простых: М(Х)>Q0 ; М(Х) < Q0 На основе выборки принимают либо основную гипотезу Н0 , либо конкурирующую Н1. Правило , по которому отклоняют или принимают гипотезу называют статистическим критерием. Основной принцип проверки гипотезы: · Выполняется выборка из генеральной совокупности · Она разбивается на 2 непересекающихся подмножества. (Область, для которой выполняется гипотеза Н0 и область, для которой выполняется гипотеза Н1) · Проводится вычисление статистики выборки. Если полученная статистика попадает в область выполнения гипотезы , то гипотеза принимается. При статистической проверке гипотезы могут быть получены ошибки 2- ух видов: · Принимается гипотеза Н0, хотя на самом деле она не верна. · Отвергается гипотеза Н0, хотя она верна. Вероятность ошибки называют уровнем значимости критерия (α) Чем меньше α , тем меньше вероятность отклонить верную гипотезу. Под α обычно считают 0,05; 0,01; 0,005; 0,001 Ошибки:
Методика проверки гипотезы: Располагая выборкой формируют нулевую гипотезу (Н0) для каждого случая подбирают статистику критерия. Обычно выбирают N- нормальное распределение ; По статистике критерия и уровню значимости определяют критическую область.
Границы областей определяются из соотношения Р (
Р ( 31.Рассмотрим проверку гипотез о законах распределения. Пусть необходимо проверить, что СВ Х подчинена определенному закону. Под альтернативной гипотезой считают, что Х не подчиняется закон. Заключение о проверке гипотез делают на основе критерия согласия. Наиболее употребляемый критерий согласия Пирсона. В это случае разбивают сумму
- практические - теоретические Если практические частоты отличаются от теоретических достаточно сильно, то гипотезу отвергают. Если отличие мало, то гипотезу принимают. В качестве меры расхождения между теоретическими и практическими значениями выборки Пирсон предложил рассчитывать величину хи (
По Пирсону при n→∞ статистика Правило применения 1. Вычисляем выборочное значение 2. Выбираем уровень значимости критерия α и по табл. 3. Если Необходимым условием применения критерия Пирсона является наличие в каждом интервале не менее 5 наблюдений. При меньших значениях |
с вероятностью, близкой к единицы, можно утверждать, что разность между средним арифметическим наблюдавшихся значений случайной величины 
и математическим ожиданием этой величины 
по абсолютной величине окажется меньше сколь угодно малого числа 
при условии, что случайная величина 
— положительное число, близкое к единице.
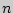независимых испытаний вероятность 
появления события 
постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности 
сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство
принимает неотрицательные значения и имеет математическое ожидание, то для любого положительного числа 
справедливо неравенство
(x), определяющая для каждого х частоту событий {X<x} называется эмпирической функцией распределения, т.е. 
(x)= nx/n, где nx- число наблюдений меньше х
>0 пределом вероятностей отклонения эмпирической функции от теоретической равно 1 ( Ɏℰ > 0 
)
= 1/n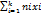 
(Среднее арифметическое элементов выборки)
– 
= 
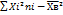
Дв
- значение признаков, находящихся на середине.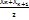
n= 2k+1 следовательно 
из n-элементов оценить неизвестный параметр ϴ (тета). Считаем, что 
параметра ϴ называется его приближенное значение, зависящее от данных выборки. Получаем, что 
, такую функцию называют статистической. Оценка 
свойств:
.
- выборка из генеральной совокупности. Тогда х выборочное среднее 
будет несмещенной и состоятельной оценкой мат. ожидания.
) = 
, т.е. выборочная дисперсия является смещенной оценкой дисперсии. Для получения несмещенной дисперсии ее исправляют.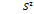
= 
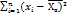Такая оценка называется и состоятельной. При больших n , 
является несмещенной оценкой вероятности события А(р(А))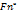
(x) – эмпирическая функция распределения является несмещенной оценкой функции распределения F(x)
, то для нахождения их оценок необходимо решить систему двух оценок 
, то для их оценок нужно решить систему их к-уравнений
ил 
случайной величины х, Фишер предложил функцию правдоподобия от аргумента ϴ
,
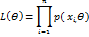
параметров ϴ берем такое значение 
max
используются как его приближенные значения, но они не говорят о том , с какой погрешностью оцениваемый параметр . Для этого необходимо найти некоторый интервал ( 
; 
), который показывает параметр 
; 
попадает в интервал. На практике в качестве γ используют стандартные значения 0,9 ; 0,95 ; 0,99 ; 0,999.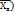
= Д (1/n 
Д ( 
= 
= 
= 
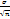. Для получения интервала оценки вспомним формулу вероятности попадания в интервал. Р ( ⃓х-а⃓ < ℰ ) = 2 Ф( 
) – функция Лапласа.
) = 2 
(t), t = 
} = 2 
} = 
: ( 
) 
, где S- исправленное среднее квадратическое отклонение.
γ = Р{ 
} Введем обозначения: 
= 
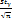Доверительный интервал: ( 
; 
)
; 
) n – объем выборки ; S – стандартное отклонение. 
и 
- квантиль 
= 
- по табл.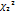
= 
; 
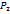) , где 
- t 
, 
, 
(t)= γ/2
- распределение Пирсона; t- распределение Стьюдента; F- распределение Фишера.
- выборка
> 
) = α
) = α/2 Р ( 
) = α/2
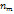
= n * 
)
= 
– n (*)
:
по формуле (*)
= 
интервалы объединяют.