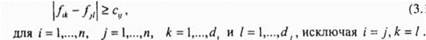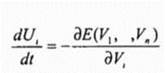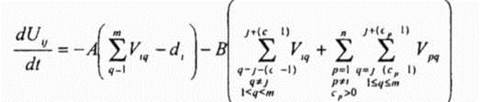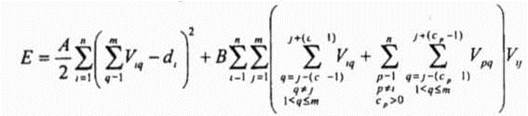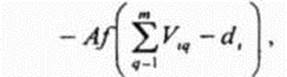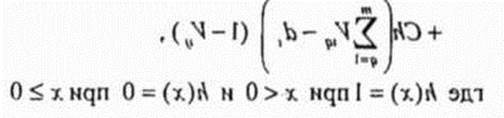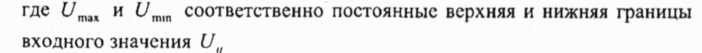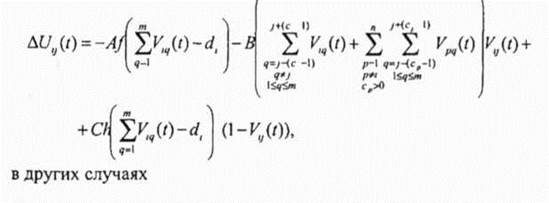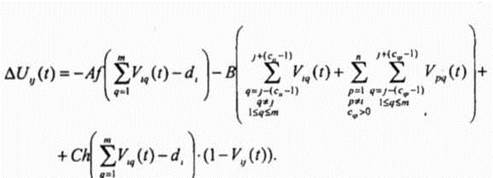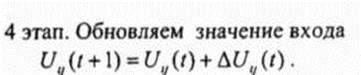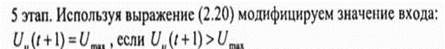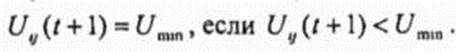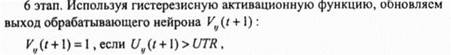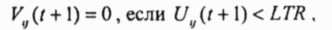ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Использование нейронных сетей для распределения каналов в сотовых радиосетях

1 2 34

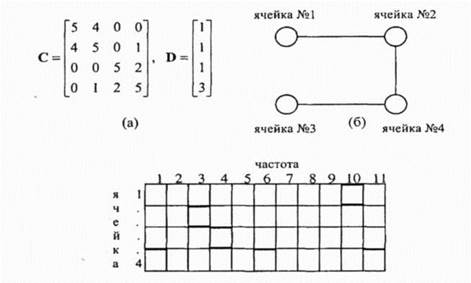
Решение задачи назначения частот, так же как и решение задачи прогнозирования напряженности поля, является одним из этапов проектирования ССПР При решении этой задачи назначение частот должно производиться в рамках ограничений заданных матрицей электромагнитной совместимости (ЭМС) При этом рассматриваются такие ограничения, как

ограничения из-за помех по соседнему каналу,

ограничения из-за помех, обусловленных совместным расположением (несущие используемые в одной ячейке, должны иметь необходимый разнос по частоте), "f

ограничения по числу частот для каждой ячейки

В 1982 г Гамет и Рейв определили общий вид задачи распределения каналов в произвольной неоднородной сотовой радиосети [61] Согласно их определению ограничения ЭМС в п -сотовой сети описываются с помощью матрицы размером пхп , которую называют матрицей совместимости С Каждый недиагональный элемент с матрицы С представляет собой расстояние минимального разнесения в частотной области между частотой, присваиваемой ; -й ячейке и частотой, присваиваемой j -й ячейке Ограничения из-за помех по соседнему каналу могут быть записаны как с_ц = 1 Запись с,. = 2 указывает на то, что частоты, смежные в частотной области не могут присваиваться смежным ячейкам, а значение с_у =0 - на то, что ячейкам / и j разрешается использовать одну и ту же частоту Каждый диагональный элемент с„ в С обозначает расстояние минимального разнесения между двумя любыми частотами, присваивае-мыми / -й ячейке. При этом для удовлетворения выше сформулированных ограничений с_и всегда должно удовлетворять ограничению с_п > 1 .

Требования, предъявляемые к частотному каналу каждой ячейки п -сотовой сети, описываются с помощью п -элементного вектора, который называют вектором спроса D. Элемент d, вектора D обозначает число частот, которые должны присваиваться i -й ячейке. Обозначая через f_lk к -ю частоту, присваиваемую /* -й ячейке, ограничения по ЭМС можно записать следующим образом:

В качестве примера, приведем решение задачи распределения каналов (рис.3.8в) для чстырехсотовой сети [101]. На рис. 3.8а приведена матрица совместимости С и вектор спроса D. На рис. 3.86 показана топология сети, соответствующая матрице совместимости С.

Рис. .8. Распределение частотных каналов для чстырехсотовой сети

Задача распределения каналов относится к математическим задачам, связанным с раскраской графов [67]. Из теории известно, что время необходимое для нахождения решения, экспоненциально увеличивается с увеличением размерности задачи (то есть, ростом числа базовых станций).

В соответствии с теорией окрашивания 1рафов, путем поиска так называемого максимально полного подграфа, можно определить нижнюю границу для общего использованного частотного ресурса. Известные алгоритмы различной степени сложности направлены на удовлетворение всех требований с учетом заданных ограничений при минимизации использованного частотного ресурса. Если в результате решения общее число рабочих частот близко к определенной нижней границе, то оно принимается, в противном случае (если спрос превышает полный частотный ресурс, выделенный для сети подвижной связи) размеры ячеек следует уменьшить (произвести их "расщепление"), чтобы сеть хотя бы локально работала с более высоким уровнем повторного использования частот.

Рассмотрим алгоритм решения задачи распределение частотных каналов, основанный на использовании искусственной НС.

Модель НС для решения комбинаторной задачи оптимизации впервые была введена Хопфилдом и Танком . Решение задачи заключается в минимизации сформированной функции энергии (см. п. 1.3.2). Несмотря на то что в ряде работ [95, 109] критиковались устойчивость и качество решения, для таких моделей известно о большом количестве успешных применений НС Хопфилда .

В 1991 г. Кунц впервые предложил использовать модель НС Хопфилда для решения задачи распределения каналов в сотовой радиосети [84]. Кунц не рассматривал ограничения из-за помех по соседнему каналу и установил предел для ограничения по расстоянию минимального разнесения между двумя любыми частотами, присваиваемыми i -й ячейке с„ = 2 . Однако, модель НС Кунца имеет несколько недостатков. Прежде всего, он использует "медленную" сигмоидальную активационную функцию. Кроме этого, в используемой функции энергии не учитываются особенности решаемой задачи. Эти недостатки модели Кунца препятствуют ее использованию для решения задачи распределения каналов в сотовой радиосети на практике.

Предлагаемая модель нейронной сети использует гистерезисную активационную функцию и модифицированную функцию энергии . Используемая функция энергии Е определяется путем рассмотрения всех ограничений, описанных выше. При этом она характеризует текущее состояние НС. Это обеспечивает более быструю сходимость решения, чем модель Кунца.

Частные производные вычислительной функции энергии E(V_t ,...,К_Л), которую также называют уравнением энергии, задают изменения входа /' -го нейрона

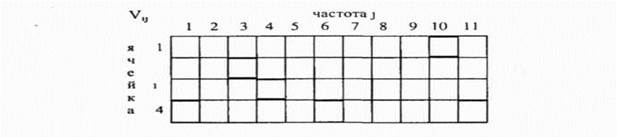
Здесь U, и V, соответственно вход и выход i -го нейрона, п - число нейронов используемых для решения конкретной задачи

На рис 3 9 в виде матрицы состояний представлены 4x11 выходов нейронов, используемых для решения задачи распределения каналов в чстырехсотовой сети, изображенной на рис 3 86, и их сходимость к решению Минимально необходимое число нейронов для решения этой задачи равно 4x11 Это следует из матрицы совместимости С и вектора спроса D, представленных на рис 3 8а (с_м = 5, d₄ = 3, следовательно,

ячейка №4 требует самое малое 11 (1+5x2) частот)

Число требуемых частот, а следовательно и необходимое для решения задачи число нейронов должно определяться перед моделированием Обычно для задач большой размерности т приблизительно может быть определено путем перемножения с_п и максимального значения в векторе спроса Если с помощью определенного таким образом значения т задача не решается, то его необходимо увеличивать до тех пор, пока система не найдет решения Однако можно воспользоваться и найденными в предыдущих работах, в частности значениями

ячейке На решении задачи, приведенной на рис 3 9, черные квадраты обозначают ненулевой выход, а белые квадраты - нулевой выход

Уравнение движения у -го обрабатывающего нейрона V_>} для п -ячеечной, Ш -частотной задачи задается следующим образом

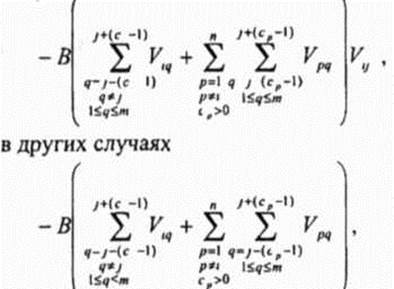
Первый член выражения (3 14) (А-член) вынуждает d_t нейронов обрабатывающих состояния т частот выделенных для i -й ячейки иметь ненулевой выход в случае, если соответствующие частоты присваиваются / -й ячейке Второй член выражения (3 14) (В-член) мешает ij -у нейрону иметь ненулевой выход в случае, если присвоение j -й частоты i -Pi ячейке нарушает следующие ограничения

имеет ненулевой выход, если присвоение j -й частоты / -й ячейке нарушает ограничении из-за помех по соседнему каналу и ограничении из-за помех, обусловленных совместным расположением

А и В являются постоянными коэффициентами (А = В = 1)

Исходя из вышесказанного, функция энергии для задачи распределения каналов в сотовой радиосети задается следующим образом

где t - число итерационных шагов, а Т и ш - постоянные параметры 3 К уравнению движения добавляется следующее выражение

Значение С выбирается на каждом итерационном шаге таким образом, чтобы устранить ситуацию, при которой два или более обрабатывающих нейрона имеют одни и те же состояния С-член помогает ij-у обрабатывающему нейрону иметь ненулевой выход, если менее чем d, нейронов для / -й ячейки имеют ненулевой выход и V - О

4 Вход обрабатывающего нейрона ограничивается двумя величинами

Для того чтобы сократить время сходимости при решении ряда задач, можно зафиксировать назначение частот для одной из ячеек или нескольких ячеек с самым большим числом требуемых частот. Например, из рис. 3.8а видно, что четвертая ячейка имеет наибольший элемент в векторе спроса, поэтому логичным является фиксирование присвоения частот этой ячейке, что и делалось при моделировании. Кроме того, фиксированное назначение частот может быть априорно заданно, например на случай расширения сети, для того чтобы не было совпадений с частотами соседних сетей.

Результаты моделирования показали, что сходимость рассматриваемого алгоритма значительно выше, например известного алгоритма Кунца [84]. Так для 25-и ячеечной сети и 73-х распределяемых частотах для решения потребовалось 200 итерационных шагов, против 2450 при использовании алгоритма Кунца.

Модификация этого алгоритма может быть направлена на учет большого количества всевозможных ограничений, которые могут быть заданы матрицей ЭМС.

Заключение

В последние десятилетия в мире отмечается быстрое развитие нейро-информациониых технологий. Актуальность исследований в этом направлении подтверждается большим количеством различных применений ней-роинформационных систем. Это автоматизация процессов распознавания образов, адаптивное управление, аппроксимация функционалов, прогнозирование, создание экспертных систем и многие другие приложения.

С помощью нейроинформационных систем можно, например, управлять телекоммуникационными сетями, проводить динамичную диагностику и терапию широкого круга заболеваний, предсказывать показатели биржевого рынка, выполнять распознавание звуковых сигналов, создавать самообучающиеся системы, способные управлять оружием и оценивать ситуацию складывающуюся на поле боя.

Особый интерес вызывает применение нейроинформационных технологий в инфотелскоммуникационных системах. Высокая эффективность нейроинформационных технологий при решении задач адаптивного управления динамичными системами может уже в ближайшее время сделать их незаменимыми при создании новых поколений сетей мобильной связи и других беспроводных сетей.

Необходимо отметить также, что в то время, как на Западе нейроин-формационные технологии применяются уже достаточно широко, в России это все еще экзотика. Это вызывает потребность с одной стороны, в повышении усилий по их популяризации, а с другой - в расширении исследований в этом направлении. Уже сейчас достаточно очевидно, что объединение нейроинформационных технологий с другими технологиями будет способствовать существенному прорыву в решении многих актуальных проблем.

Список литературы

1 Барцев С И , Охонин В А Адаптивные сети обработки информации // Препринт ИФ СО АН СССР, Красноярск, 1986, №59Б

2 Блум Ф , Лейзерсон А , Хофстедтер Л , Мозг, разум и поведение - М Мир, 1988

3 Бовбель Е И, Паршин В В Нейронные сети в системах автоматического распознавания речи - Зарубежная радиоэлектроника Успехи современной радиоэлектроники, 1998, №4, с 49-65

4 Бубенников А Н Архитектурно-технологический облик интеллектуальных нейронных сетей на кремниевых пластинах и трехмерных нейрокомпьютеров -Зарубежная радиоэлектроника Успехи современной радиоэлектроники, 1998, №4, с 34-51

5. Комашинский В И , Смирнов Д А , Титов А А , Шнурснко С А Алгоритм децентрализованного управления доступом для сети радиосвязи с пакетной передачей сообщений /53 НТК Тезисы докладов - СПб НТОРЭС им А С Попова, 1998, с 40

6. Комашинский В И , Смирнов ДА Введение в нейро-информационные технологии - СПб Тема, 1999

7. Комашинский В И , Смирнов Д А , Шнуренко С А Интегральное обслуживание пользователей в сотовых системах подвижной радиосвязи при множественном доступе с кодовым разделением /51 НТК Тезисы докладов - СПб ГУТ, 1998, с 58

8. Комашинский В И, Смирнов Д А Гибридные методы множественного доступа к беспроводным ATM сетям /54 НТК Апрель 1999 г Тезисы докладов -СПб НТОРЭС имени А С Попова, 1999, с 66-67

9. Куссуль Э М Ассоциативные нейроподобные структуры - Киев Наукова думка, 1990

10. Шаров А Н , Степанец В А , Комашинский В И Сети радиосвязи с пакетной передачей информации - СПб ВАС, 1994

1 2 34