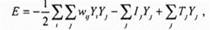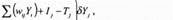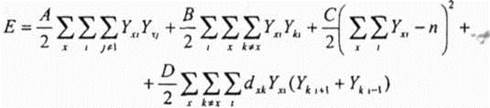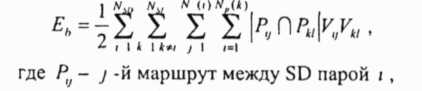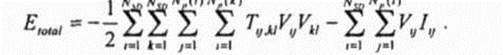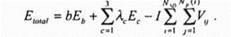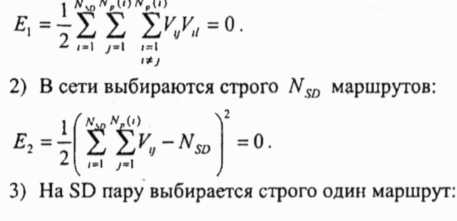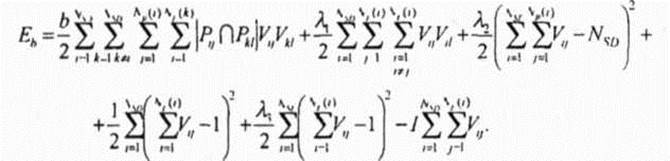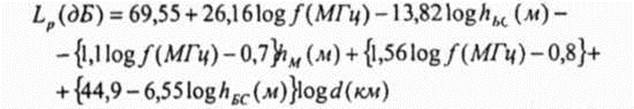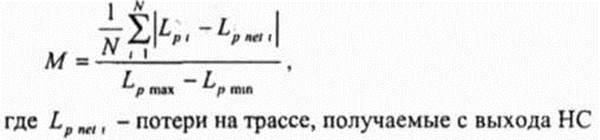ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Использование нейронных сетей для решения задач маршрутизации

1 234

Маршрутизация является одной из важных задач для телекоммуникационных сетей различного назначения Задачи, связанные с выбором маршрута, планированием работы средств связи и т п , относятся к классу сложных комбинаторно-оптимизационных задач, как правило, не имеющих простых аналитических решений Кроме того, сложность необходимых вычислений экспоненциально возрастает при увеличении количества узлов в сети Поэтому в настоящее время широко применяют различные эвристические алгоритмы и процедуры, полученные путем творческого поиска, интуиции и опыта исследователя Альтернативой существующим методам решения задач маршрутизации является использование нейросетевых моделей, которые позволяют при значительном снижении временных затрат получить хорошие субоптимальные решения Так, для решения комбинаторно-оптимизационных задач широко используются модели построенные на основе НС Хопфилда, впервые примененные для решения задачи о коммивояжере Эти модели явились началом развития нейронных методов решения сложных оптимизационных задач Большинство последующих исследований так или иначе базировались именно на них

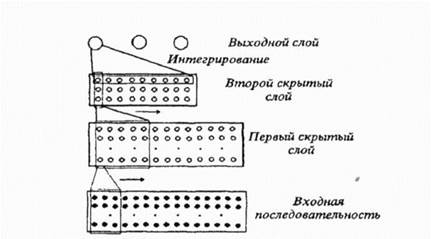
Рисунок 3. Архитектура НСВ3

Коротко остановимся на формулировке и основных принципах организации вычислений при решении задачи коммивояжера

Для некоторой группы городов с известными расстояниями между ними требуется найти кратчайший маршрут посещения каждого города один раз с возвращением в исходную точку

Обозначим города, которые необходимо посетить, буквами А, В, С , а расстояния - d_AB, d_Ac d_Bc Решением является упорядоченное множество из п городов Последовательность, в которой обходятся города удобно представлять матрицей пхп , строки которой соответствуют городам, а столбцы номерам городов в последовательности Например, имеется пять городов А, В, С, D, Е, а последовательность обхода этих городов задана матрицей


А
В
С
D
Е

(3 1)

Таким образом город С посещается первым, город А - вторым и т д Длина маршрута равна dcA+ d_AE +…. + dc В каждом столбце и в каждой строке этой матрицы может быть только одна единица, так как в каждый момент посещается только один город и каждый город посещается только один раз Матрицу вида (3 1) можно воспринимать как состояние нейронной сети из N / п² нейронов Задача состоит в том, чтобы из nмаршрутов выбрать один с наименьшей длиной Состояние каждого нейрона описывается двумя индексами, которые соответствуют городу и порядковому номеру его посещения в маршруте Например, К = 1 показывает, что город х был j -м по порядку городом маршрута

Запишем функцию вычислительной энергии для сети, предназначенной для решения задачи коммивояжера, в которой состояние с наименьшей энергией соответствует самому короткому маршруту В общем виде такая функция для рассматриваемой сети может иметь следующий вид

где Е - искусственная энергия сети, w_tj - вес от выхода нейрона / к входу нейрона j , У_у- выход нейрона j , /_у - внешний вход нейрона j , Г_у -порог нейрона j

Изменение энергии, вызванное изменением состояния j -нейрона, можно вычислить следующим образом

где 5Yj - изменение выхода j -го нейрона

Каждому состоянию системы соответствует конкретная величина вычислительной энергии Устойчивое состояние имеет меньшую энергию, чем неустойчивое Эволюция системы во времени - это движение в пространстве состояний в поисках минимума энергии и остановка в этой точке

Для рассматриваемой системы функция энергии должна удовлетворять следующим требованиям [32] Во-первых, она должна поддерживать устойчивые состояния в форме матрицы (3 1) Во-вторых, из всех возможных решений функция энергии должна поддерживать тс, которые соответствуют коротким маршрутам Этим требованиям удовлетворяет функция энергии вида (при этом, Y_XJ = 0,1)

Первые три члена выражения (3 4) поддерживают первое требование, четвертый член - второе, А, В, С, D - положительные множители Первый член равен нулю, если каждая строка х содержит не больше одной единицы Второй член равен нулю, если каждый столбец содержит не более одной единицы Третий член равен нулю, если в матрице вида (3 1) п единиц Таким образом, без учета четвертого члена функция энергии имеет минимумы (Е = 0) во всех состояниях, представленных матрицей с одной единицей в каждом столбце и каждой строке Все другие состояния имеют более высокую энергию Короткие маршруты поддерживает четвертый член В нем индексы j берутся по mod л, для того чтобы показать, что ; -й город соседствует в маршруте с (п-1)-м н первым, т е У₄ = Y^ Четвертый член численно равен длине маршрута

Раскрывая скобки в (3 4) и приравнивая коэффициенты при квадратичных и линейных членах в полученном выражении и общей формуле энергии (2 2). опоелелясм матоицу связей и внешние взаимодействия

нальных состояний соответствует самому короткому маршруту

Рассмотрим вариант совместного решения задачи маршрутизации и планирования использования линий радиосвязи для сети пакетной радиосвязи с многоскачковой топологией Важность взаимосвязи между маршрутизацией и вопросами планирования последовательности выбора направления для передачи по используемым линиям связи показана в [65] Там же обобщен случай непрерывного трафика для определенного класса сетей При этом выбор маршрутов максимизирующих степень узла в сети, позволяет спланировать работу так, чтобы время ее выполнения было минимальным Степень узла для этого случая, определяется как сумма всех потоков, поступающих в узел и исходящих от узла Например, линия, которая должна активироваться, три раза добавляет поток из трех единиц к обоим узлам, которые она соединяет При этом, критерий качества работы, выбираемый для задачи маршрутизации, должен отражать цели, связанные с соответствующей задачей составления плана работы линий связи

Пусть заданы граф связности сети пакетной радиосвязи, ряд пар N_SD -исходная точка - пункт назначения (SD) и ряд линий связи, соединяющих каждую пару SD Предполагается, что в системе используется тактированный множественный доступ и длительность временных окон соответствует длине пакета (все пакеты имеют фиксированную длину), а на каждом узле имеется только один приемопередатчик Между каждой парой узлов сети SD имеет место одинаковый трафик, равный одному пакету на цикл передачи Считаем также, что линии связи между соответствующими парами узлов активизируются (используются для передачи) по мере необходимости

Требуется выбрать единственный маршрут между каждой парой SD с таким расчетом, чтобы минимизировать желаемый критерий качества работы

Показатель качества работы должен согласовываться со структурой НС Хопфилда По аналогии с рассмотренной выше задачей коммивояжера такой показатель, называемый "энергией перегрузки" задается формулой

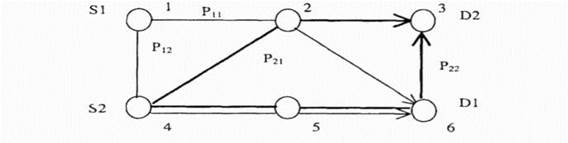
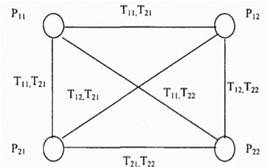
Цель состоит в минимизации Е_ь с учетом того, что для каждой пары SD выбирается только один маршрут (те V_y = 1 для единственного значения у для каждого значения /) В этом случае энергия перегрузки соответствует сумме числа общих узлов всех выбранных маршрутов (одного для каждой SD пары), взятых попарно Например, на рис 3 4 показана простая сеть пакетной радиосвязи с шестью узлами и двумя маршрутами между каждой из двух SD пар

Рисунок 4

гию перегрузки E_h = 1, так как эти маршруты имеют один общий узел (узел 6).

Теперь рассмотрим модель НС Хопфилда, используемую в этом случае для выбора маршрута между несколькими SD парами в сети пакетной радиосвязи. Выходные напряжения нейронов (которые и определяют их состояния) такой НС приближаются к двоичным значениям по мерс перехода сети к состоянию устойчивого равновесия с минимальной "энергией". Соединения между нейронами i и j описываются весом Т_ч, который

положителен если соединение возбуждающее и отрицателен, если соединение тормозящее (запрещающее). В рассматриваемой модели НС для каждого маршрута между каждой SD парой определяется один нейрон. Вариант модели НС для сети изображенной на рис. 3.4 представлен на рис. 3.5. В соответствии с рис. 3.5 нейрон ij отображает j маршрут между SD парой I.

НС эволюционирует от какого-то начального состояния до состояния равновесия, которое отображает минимум (не обязательно глобальный) функции энергии Ляпунова, которая по аналогии с (3.2) может быть записана через веса соединений, токи смещения и напряжения на выходах нейронов следующим образом [111]:

для энергии перегрузки, определяемое с помощью выражения (3.6), применимо в полной мере только для аналоговой реализации системы.

Рис..5. Модель НС дл* ист, и-юбраженной на рис. 2.4

Рассматриваемая задача оптимизации с целым рядом ограничений может быть сведена к задаче без ограничений за счет включения ограничений в целевую функцию посредством использования множителей Ла-гранжа Функция энергии перегрузки при этом приобретает следующий вид:

Ограничения для задачи являются соответствующими членами уравнения энергии перегрузки Е_с (равны нулю, если ограничение выполняется) и формулируются так:

1) На SD пару активизируется (выбирается) не более одного маршрута:

Хотя последнее ограничение представляется избыточным (выполнение первых двух гарантирует удовлетворение последнего), его включение в уравнение энергии полезно для достижения более быстрой сходимости.

Подстановка выражений для Е_ь и Ј_t в (3.8) дает:

Одним из самых важных вопросов при разработке модели НС Хоп-филда и дальнейшем моделировании работы системы является вопрос выбора коэффициентов A_t. Фактически, любые значения Л, приведут к получению справедливых выражений для Е_1пш1. Однако при эволюции системы может быть гарантирован только локальный минимум, то есть конечное состояние зависит от начального состояния, при котором начинается эволюция системы. Таким образом, различные значения коэффициентов приводят к получению различных результатов. В большинстве исследований, посвященных использованию НС Хопфилда величины коэффициентов полагаются постоянными, лучшие значения которых обычно определяются в ходе испытаний при программном моделировании. Однако существует ряд подходов, позволяющих во всей полноте использовать метод множителей Лагранжа . В этом случае величины Х_с изменяются по мере изменения состояния системы

Оценить качество решения задачи обычно не представляется возможным, так как число возможных решений для больших сетей очень велико. Например, для 100-узловой сети существует приблизительно 510³⁵ различных решений. Поскольку исчерпывающий поиск для такой сети исключается, то при моделировании выполнялся случайный поиск 2-Ю⁶ выборок решений для получения опорного уровня качества работы для оценки работы НС . Наилучшее решение, полученное с помощью случайного поиска, имело энергию перегрузки Е_ь - 567 . Использование традиционных эвристических методов решения задачи маршрутизации позволило получить £_А=313. Наилучшее решение найденное с помощью НС Хопфилда дало Ј_fc = 291. Наибольшее значение энергии перегрузки в этом случае было E_h - 303. Моделирование выполнялось от 50 различных начальных состояний. Таким образом, результаты моделирования показывают эффективность рассмотренной модели для минимизации перегрузки в больших сетях. Тот факт, что глобальный минимум находится не всегда, скрашивается тем обстоятельством, что возможно осуществление нескольких испытаний при различных начальных условиях, так что найденное наилучшее решение может выбираться в качестве решения задачи.

Большое количество работ посвященных использованию НС при решении задачи маршрутизации и близость получаемых результатов к оптимальным свидетельствуют о робастности таких моделей.

3.4. Использование нейронных сетей при планировании сотовых сетей подвижной радиосвязи

Одним из основным этапов проектирования сотовых сетей подвижной радиосвязи (ССПР) является этап территориального планирования, в ходе которого выбираются структура (конфигурация) сети, места размещения базовых станций (БС), рассчитываются возможность обеспечения охвата (покрытия) требуемой зоны обслуживания с заданным качеством связи и емкость сети, требуемая для обслуживания абонентской нагрузки с заданной интенсивностью потерь (отказов в обслуживании).

В качестве технических основ планирования используются характеристики стандартов ССПР, характеристики приемо-передающего оборудования и антенн, условия распространения радиоволн, требуемая напряженность поля полезного сигнала, средняя нагрузка на одного абонента, допустимое значение вероятности блокирования вызовов [3].

Таким образом, прогнозирование напряженности поля в зоне обслуживания БС является одним из этапов планирования современных систем подвижной связи. В настоящее время широко используются две стратегии прогнозирования напряженности электрического поля. Одна из них состоит в выводе эмпирических формул на основе измерений, а другая основывается на аналитических моделях, использующих теорию дифракции. Практика показывает, что и та и другая модели имеют ряд недостатков [2].

Использование эмпирического метода прогнозирования напряженности поля, основанного на использовании нейронных сетей, позволяет устранить некоторые недостатки [102]. В этом случае НС решает задачу аппроксимации некоторой функции по имеющимся значениям ряда точек. Для НС эти точки являются обучающим множеством. Кроме известныхзначений средней напряженности электрического поля на вход НС подается приведенная к дискретной форме и нормализованная информация о покрове земной поверхности, рабочей частоте, высоте антенн и т д Параметры НС настраиваются таким образом, чтобы для любой входной комбинации погрешность значения формируемого на выходе НС была минимальна Выход сети в зависимости от требований может определяться в виде нормализованной напряженности поля в заданной точке, в виде потерь на трассе и др Динамический диапазон напряженности поля во многом определяется распространением радиоволн в свободном пространстве Для повышения точности аппроксимации среднего значения напряженности поля, вклад последнего может вычисляться аналитически и исключаться из процесса обучения

Результаты использования НС для прогнозирования напряженности поля можно рассмотреть на следующих примерах

В первом случае используется хорошо известная формула Хата , отражающая эмпирическую аппроксимацию потерь при распространении L в городских районах

Диапазон частот / = 150 1500 МГц, высота расположения базовых станций (БС) h_BC = 30 200 м , высоты расположения подвижных станций h_M =1 10м и дальность d = 1 20км Нейронная сеть, используемая для аппроксимации формулы имела четыре нейрона во входном слое и десять нейронов в скрытом слое Выход моделируемой сети отображает потери при распространении L_p

Применение НС для прогнозирования напряженности поля поясняется на рис 3 6

Нормализованная средняя ошибка моделирования М определяется следующим обпазом

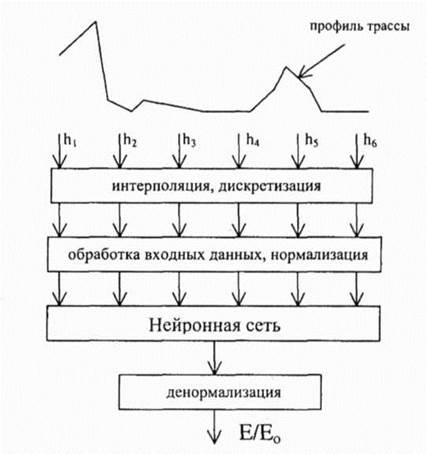
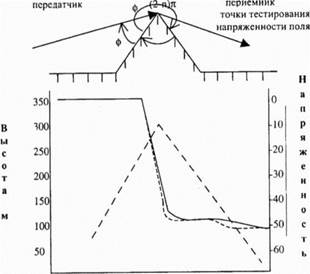
Рис6 Вариант применениеНС для прогнозирования напряженности поля

После 1200 циклов обучения на примере обучающего множества из 2160 точек среднее отклонение составило приблизительно 0,18% Для точек тестирования, выбранных между точками обучения в рассматриваемом параметрическом пространстве, отклонение увеличивается до 0,24%, при этом М_тах < 1,23% В этом эксперименте динамический диапазон составляет L_p _max - L_p _min = 1ЪОдБ

Другая типичная задача связана с использованием геометрической теорией дифракции Келлера [80] для случая дифракции на клине (см рис 3 7а) При этом также может использоваться многослойная НС с одним скрытым слоем Число нейронов во входном и скрытом слое выбирается исходя из задачи и предъявляемых к решению требований

В модели для аппроксимации нормализованной напряженности поля ЕI Е_а на профиле трассы изображенной на рис 3 7а использовалась НС, имеющая 11 нейронов во входном слое и 8 нейронов в скрытом слое

О 1 2 3 4 5 6 7 8 9 10 дБ

Расстояние, км

------- _ вычислено по формуле Келлера

_ - аппроксимация НС

топография профиля

Рис 7 Аппроксимация напряженности поля с помощью нейронной сети

Выборка топографических данных производилась в 10 точках, которые обеспечивают входные данные для 10 элементов Величина выборки может изменяться Данные о ней поступают на 11 вход В результате последней операции выборка приспосабливается к длине профиля трассы Моделирование проводилось для различных комбинаций высот, углов участков препятствия моделируемого "клином" Среднее отклонение вычислялось по формуле (3 11) и после 20 ООО циклов обучения составило 0,3% В обоих случаях при обучении использовался алгоритм обратного распространения На практике для обучения НС могут использоваться как результаты аналитических расчетов, так и результаты текущих и ранее

проведенных измерений После завершения процесса обучения для тестовых примеров максимальное отклонение М_таж не превышало 6% (см рис 3 7)

Таким образом, подтверждается возможность использования НС для прогнозирования напряженности поля на этапе планирования современных систем подвижной связи и в других случаях В целях повышения точности прогнозирования рассмотренные нейросетевые модели могут совершенствоваться Так, может более полно учитываться вся имеющаяся картографическая информация, информация о земном покрове и др

1 234