 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Расчет монтажных напряжений
В статически неопределимой стержневой системе
l1 = 0,8 м; l2 = 1,2 м; k = 0,6; D = 0,8 мм; стержни стальные Е = 2∙105 МПа; sт= 650 МПа; a = 30º; b = 45°. 1. Статическая сторона задачи Составим статические уравнения равновесия (рис. 3.5.2).
Для узла K:
или Получили два уравнения
2. Геометрическая сторона задачи
полученное уравнение является уравнением совместности перемещений. 3. Физическая сторона задачи По закону Гука для упругих систем удлинения стержней равны:
Подставим эти выражения в уравнение совместности перемещений, получим
в результате преобразований
после подстановки числовых данных получим:
4. Расчет усилий в стержнях (синтез) Система разрешающих уравнений имеет вид:
преобразуем
после подстановки в первое уравнение получим 4,86NBC = 1,41EAD, откуда
тогда напряжение
усилие в стержне ВK:
тогда напряжение усилие в стержне KL:
тогда напряжение Находим силы, действующие в стержнях. Стержень BC:
Стержень BK:
Стержень KL:
Расчет на прочность Определим напряжения в стержнях. Для стержня ВС:
Для стержня BK:
Для стержня KL:
Максимальные напряжения возникают в стержне ВK
Условие прочности имеет вид
где n – коэффициент запаса прочности. Для сталей n = 1,5¸2,5, примем n = 2, тогда допускаемые напряжения Условие прочности для заданной стержневой системы выполняется:
Задача 7.Жесткий брус шарнирно прикреплен к фундаменту и удерживается двумя стальными тягами одинакового поперечного сечения.
Решение После сборки конструкции зазор D лишь частично перекрывается удлинением левого стержня, тогда жесткий брус ВС поворачивается в шарнире D, вызывая удлинение правой тяги. В сечениях тяг появляются продольные силы, а в шарнире D две реакции xD и yD. Задача статически неопределима, поскольку для 4 неизвестных усилий существует только 3 уравнения статического равновесия. Решение проводим по стандартной схеме. 1. Статическая сторона задачи
тельно шарнира D (рис. 3.5.5):
после преобразований получим 0,447Nпр – 0,832Nл = 0.
2. Деформационная сторона задачи Для составления уравнения совместности перемещений рассмотрим деформированное состояние системы после сборки (рис. 3.5.6).
Из подобия треугольников DDBB2 ~ DDCC1
ВВ2 = 3СС1; из DВВ2В3: из DСС1С2: Подставляя, получим 0,894(D - Dlл) = 1,665Dlпр, полученное уравнение является уравнением совместности перемещений. После преобразований: D = Dlл + 1,862Dlпр. 3. Физическая сторона задачи По закону Гука где
Подставляя в преобразованное уравнение совместности перемещений, получим:
тогда 0,002ЕА = 1,803Nл + 2,082Nпр. 4. Синтез Система разрешающих уравнений
Решаем систему простой подстановкой Nпр = 1,86 Nл, 2,082×1,86 Nл +1,803 Nл = 0,002ЕА;
где Е = 2×105 МПа, тогда возникшие после сборки напряжения в стержнях:
|



 Рис. 3.5.1
Рис. 3.5.1
 Рис. 3.5.2
Рис. 3.5.2 ;
;  ;
;  ;
;  или
или  .
. ;
;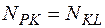 ;
; ;
;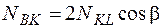
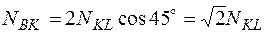 .
. ,
, с тремя неизвестными.
с тремя неизвестными. Рис. 3.5.3
Рис. 3.5.3 ;
;  ;
;  ;
;  ;
;  ;
;  ;
; ,
, ,
, ,
, .
. .
. ,
, .
.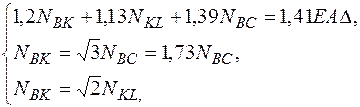
 ,
, ,
, МПа.
МПа. ,
, МПа.
МПа. ,
, МПа.
МПа. .
. .
. .
. МПа.
МПа. МПа.
МПа. МПа.
МПа. МПа.
МПа. ,
, МПа.
МПа.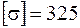 МПа.
МПа. Рис. 3.5.4
Рис. 3.5.4 Рис. 3.5.5
Рис. 3.5.5 , где
, где ,
, ,
, Рис. 3.5.6
Рис. 3.5.6 , тогда
, тогда ,
, .
. ;
; 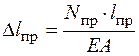 ,
, ,
, .
. , где D = 0,002l,
, где D = 0,002l,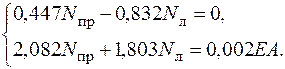
 ,
, ,
, МПа.
МПа. МПа.
МПа.