 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Расчет на жесткость стержня постоянного сечения
Растяжение Краткие теоретические сведения и простейшие задачи
Растяжением называется вид нагружения, при котором в поперечном сечении стержня возникает единственный внутренний силовой фактор – продольная сила, являющаяся равнодействующей нормальных напряжений, равномерно распределенных по сечению.
Условие прочности Для проведения проверочного расчета необходимо, по известным внешним силам и размерам сечения вычислить нормальные напряжения s и проверить выполнение условия прочности. При проектировочном расчете необходимо по известным внешним силам и известным характеристикам материала определить из условия прочности размеры поперечного сечения.
Пример 1
Решение Рассечем стержень СД и рассмотрим равновесие части, содержащей стержень ВС.
Составим уравнения статического равновесия
С точки зрения расчета на прочность нет необходимости определять реакции шарнира В. Из суммы моментов относительно опоры В получаем:
из условия прочности
откуда Минимальная площадь сечения, обеспечивающая прочность стержня 139,375 мм2 = 140 мм2.
Пример 2 Жесткий стержень ВС загружен по всей длине распределенной нагрузкой интенсивности q = 10
Решение
Напряжение, возникающее в стержне СD,
Запас конструкции Запас достаточен. Определим вертикальное смещение т. С. Под действием распределенной нагрузки на жесткий стержень ВС, последний поворачивается в шарнире В на угол j (рис. 3.6). Тогда стержень СD укорачивается на величину DlCD = CC2.
тогда
Расчет на прочность и жесткость ступенчатого стержня при осевом растяжении
Пример. Для заданной схемы нагружения ступенчатого стержня определить из расчета по допускаемым напряжениям параметр площади сечения А, обеспечивающий его прочность. Проверить жесткость стержня, при необходимости скорректировать параметр площади.
F = 10 кН, q = 20 кН/м, l1 = 0,6 м, l2 = 0,8 м, l3 = 1,2 м, ст. 45, sт = 340 МПа. Определим реакцию в защемлении R
R = 20 + 20×1,8 = 56 (кН). Основные этапы расчета 1. Построение эпюры продольной силы. 2. Построение эпюры сравнительных напряжений, определение положения опасного сечения. 3. Определение параметра площади А из расчета на прочность по допускаемым напряжениям. 4. Определение перемещений и построение эпюры перемещений. Проверка жесткости. 3.2.1. Построение эпюры продольных сил.Эпюра продольных сил строится методом сечений. Рассмотрим три участка (рис. 3.7). Участки выбирают так, чтобы в пределах участка продольная сила описывалась одной функцией или сохраняла постоянное значение. I участок. Рассечем стержень по сечению I-I и рассмотрим левую часть. За переменную длины z1 возьмем расстояние от защемления (неподвижного сечения) до сечения 0 £ z1 £ l1 (рис. 3.8).
N1(z1) найдем из уравнения статического равновесия оставленной части:
Для построения прямой необходимо две точки. Определим значение продольной силы на границах участка. N1(0) = F + q×l1 = 10 + 20×0,6 = 10 + 12 = 22 (кН), z1 = 0 соответствует защемлению N1(l1) = F = 10 кН, z1 = l1 соответствует левому торцу. Нанесем полученные значения на эпюру (рис. 3.7, а). II участок. Рассечем стержень по сечению II-II и рассмотрим левую часть. Z2 обозначим расстояние от защемления до сечения
N2 = F + ql1 - R = 10 + 20×0,6 – 56 = -34 (кН). Продольная сила на втором участке постоянная, сжимающая, равная -34 кН (рис. 3.7, а). III участок. Рассечем стержень по сечению III-III и рассмотрим правую часть. За z3 примем длину от начала участка. Длина оставленной части (l3 – z3), где 0 £ z3 £ l3 (рис. 3.10).
F - q×(l3 – z3) – N3×(z3) = 0, откуда
Для построения прямой вычислим значения N3×(z3) на концах участка N3(0) = F - q×l3 = 10 - 20×1,2 = -14 (кН), N3(l3) = F = 10 кН, z3 = 0 соответствует границе II и III участков, z3 = l3 соответствует правому торцу (рис. 3.7, а). 3.2.2. Определение параметра площади поперечного сечения.Для определения параметра площади поперечного сечения А необходимо выявить положение опасного сечения. Опасным является сечение, в котором возникают наибольшие напряжения. Нормальные напряжения в сечениях растянутого стержня распределяются по площади сечения равномерно и могут быть вычислены: Построим эпюру сравнительных напряжений (сохраняя в знаменателе А). На первом участке напряжения
зависимость напряжений от координаты длины линейная. Для построения прямой найдем значения напряжений на границах участка
Аналогично на втором участке, где продольная сила постоянна,
На третьем участке:
Найдем значения на границах участка
Построим эпюру сравнительных напряжений (рис. 3.7, б). Опасное сечение в защемлении со стороны первого участка
Площадь А найдем из условия прочности
n – коэффициент запаса; если материал пластичный sоп = sт, n = 1,5 ¸ 2,5, если материал хрупкий sоп = sв, n = 3 ¸ 5, сталь 45 – материал пластичный sоп = sт = 340 МПа; тогда, выбирая коэффициент запаса n = 2, получим допускаемое напряжение По условию прочности
Минимальная площадь, обеспечивающая прочность А = 129,4 мм2 @ 130 мм2. Построим эпюру истинных напряжений:
По найденным значениям напряжений построим эпюру истинных напряжений (рис. 3.7, в). Для проверки жесткости нужно вычислить перемещения торцевых сечений: W(l2 + l3) и W(l1). Они не должны превосходить допускаемых перемещений [Dl] = 0,001L, где L – длина, на которой оцениваемое перемещение получено. Для заданного стержня на левом торце W(l1) £ 0,001× l1, на правом торце W(l2 + l3) £ 0,001(l2 + l3). Перемещение любого сечения можно определить по закону Гука
Рассмотрим первый участок:
Найдем перемещения на концах участка
W1(l1) = 0,00037 м = 0,37 мм. Зависимость параболическая Рассмотрим второй участок:
Значения на концах участка
W2(z) – линейная функция (рис. 3.7, г). Третий участок:
W3(l3) = 0,64 мм,
Заметим, что функция продольной силы является производной от функции перемещения. На третьем участке продольная сила пересекает ось, следовательно, функция перемещения имеет экстремум (минимум). Найдем координату точки экстремума
Эпюра перемещений (рис. 3.7, г). Проверяем жесткость: допускаемое перемещение на левом торце [Dl1] = 0,001×0,6 = 0,0006 м, перемещение W(l1) = 0,00037 м < 0,0006 м, условие жесткости выполняется. На правом торце Полученное перемещение 0,00076 м < 0,002 м, условие жесткости выполняется.
Расчет на жесткость стержня постоянного сечения Выполнить расчет на прочность и жесткость стержня постоянного сечения, представленного на рис. 3.11.
расчет на жесткость при растяжении состоит в проверке выполнения условия жесткости торцевых сечений. Для рассматриваемого стержня
где W0 – перемещение точки отсчета. Поэтому найдем функции продольной силы на участках стержневой системы и построим эпюру продольной силы. Причем переменную длины z выгодно выбирать от начала участка в направлении от неподвижного сечения (защемления). Определим реакцию в защемлении R из уравнения статического равновесия стержня:
I участок. Рассечем стержень по сечению i-i и оставим левую часть длиной (l1-z1), где
значения на концах участка
II участок. Рассечем стержень по сечению iI-iI и рассмотрим левую часть, координату z2 возьмем от защемления
N2 = 20×0,6 -18 = -6 (кН). эпюра (рис. 3.11, а). III участок. Рассечем стержень по сечению iII-iII и рассмотрим правую часть (z3 выберем от начала участка) (рис. 3.14).
Значения на концах участка:
Эпюра (рис. 3.11, а). Стержень должен быть прочным, поэтому сначала назначим площадь поперечного сечения из условия прочности Поскольку сечение постоянно, максимальное напряжение достигается в том же сечении, в котором максимальна продольная сила. Для рассматриваемого стержня
Построим эпюру перемещений.
параболическая функция. Точка отсчета неподвижна, поэтому W0 = 0. Найдем перемещение левого торца и распорядимся кривизной.
Перемещение второго участка.
На третьем участке точка отсчета z3 является концом второго участка, поэтому
значения на концах участка W3(0) = -0,00051 м.
Уточним вид эпюры перемещений: продольная сила является производной функции перемещения по координате длины, следовательно, в точках пересечения эпюрой продольной силы оси (N(z) = 0) перемещение может иметь экстремум, в рассматриваемом случае минимум. Найдем Wmin. Определим точку экстремума из уравнения
Построим эпюру (рис. 3.11, б), учитывая, что на первом участке Проверка жесткости: левый торец
Таким образом, минимальная площадь сечения, обеспечивающая прочность рассмотренного стержня, обеспечивает и его жесткость. Примечание. Если на каком-либо торце условие жесткости не выполняется, необходимо корректировать параметр площади из условия жесткости:
|



 Рис. 3.1
Рис. 3.1 , где s - нормальное напряжение, А – площадь поперечного сечения.
, где s - нормальное напряжение, А – площадь поперечного сечения. , где
, где  - допускаемое напряжение
- допускаемое напряжение  , где sпред – предельное напряжение.
, где sпред – предельное напряжение.  - для пластичного материала n = 1,5¸2,5.
- для пластичного материала n = 1,5¸2,5.  - для хрупкого материала n = 3¸5.
- для хрупкого материала n = 3¸5.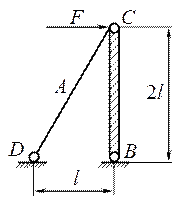 Рис. 3.2
Рис. 3.2 Рис. 3.3
Рис. 3.3 ;
; ;
; .
.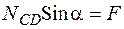 , тогда
, тогда  ;
;  ;
;  , тогда
, тогда  ,
, кН,
кН, ,
, МПа,
МПа, мм2.
мм2. .
. Рис. 3.4
Рис. 3.4 Рис. 3.5
Рис. 3.5 или
или  , откуда
, откуда кН.
кН. МПа.
МПа. .
. Рис. 3.6
Рис. 3.6 , где NCD – продольная сила в стержне CD, lCD – длина стержня CD,
, где NCD – продольная сила в стержне CD, lCD – длина стержня CD,  ,
, мм,
мм, мм.
мм. Рис. 3.7
Рис. 3.7 ,
, ,
, Рис. 3.8
Рис. 3.8 , откуда
, откуда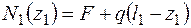 - линейная функция.
- линейная функция. Рис. 3.9
Рис. 3.9 Рис. 3.10
Рис. 3.10 - линейная зависимость.
- линейная зависимость. , где N(z) – продольная сила в сечении;
, где N(z) – продольная сила в сечении; ;
; ;
;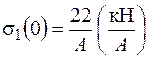 ;
;  .
. .
. .
. ;
; .
. .
. , где
, где  , где
, где  - опасное для материала напряжение,
- опасное для материала напряжение, МПа.
МПа. , откуда
, откуда  м2.
м2. МПа;
МПа; МПа;
МПа; МПа;
МПа; МПа;
МПа; МПа.
МПа. , где W0 – перемещение точки отсчета.
, где W0 – перемещение точки отсчета. .
. ;
; ;
; ;
;  - выпуклая функция (рис. 3.7, г).
- выпуклая функция (рис. 3.7, г). .
. ;
; ;
;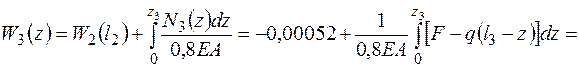
 - функция параболическая,
- функция параболическая,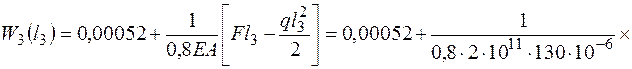

 м,
м, - парабола вогнутая.
- парабола вогнутая. , откуда
, откуда  м,
м,

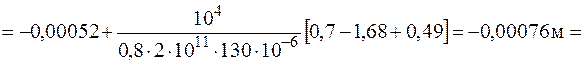
 мм.
мм.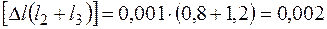 м.
м. Рис. 3.11
Рис. 3.11 и
и  , где
, где  , где L – длина, на которой оцениваемое перемещение получено. Перемещение W(z) может быть получено по закону Гука
, где L – длина, на которой оцениваемое перемещение получено. Перемещение W(z) может быть получено по закону Гука ,
, , откуда
, откуда  кН.
кН.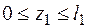 .
. Рис. 3.12
Рис. 3.12 - линейная функция.
- линейная функция.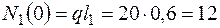 кН;
кН;  эпюра (рис. 3.11, а).
эпюра (рис. 3.11, а). (рис. 3.13).
(рис. 3.13). Рис. 3.13
Рис. 3.13 Рис. 3.14
Рис. 3.14 . Из уравнения статического равновесия (суммы сил вдоль оси z)
. Из уравнения статического равновесия (суммы сил вдоль оси z)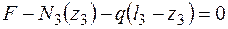 , откуда
, откуда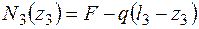 – линейная функция.
– линейная функция. (кН);
(кН);  (кН).
(кН). ,
, МПа, откуда
МПа, откуда  мм2.
мм2. –
–
 м = 0,5 мм.
м = 0,5 мм. - линейная функция.
- линейная функция.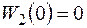 - сечение защемлено.
- сечение защемлено.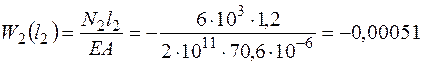 м = -0,51 мм.
м = -0,51 мм.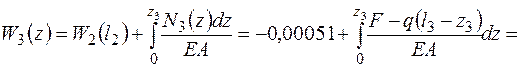
 ,
,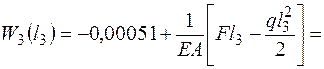
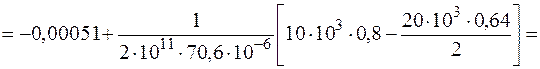
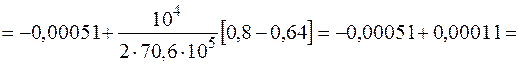
 мм.
мм. , откуда
, откуда м.
м.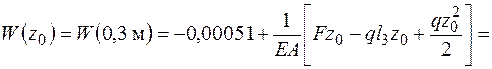
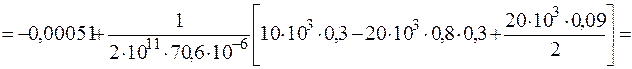
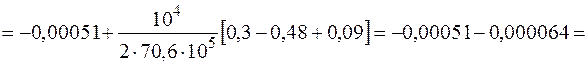
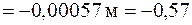 мм.
мм. мм;
мм; мм < 0,6 мм – условие жесткости выполняется. правый торец:
мм < 0,6 мм – условие жесткости выполняется. правый торец: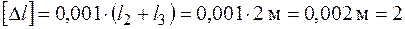 мм;
мм; мм < 2 мм – условие жесткости выполняется.
мм < 2 мм – условие жесткости выполняется. .
.