 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Статически неопределимые стержневые системы
Стержневые системы, для которых реакции связей не могут быть определены из уравнений статического равновесия, называются статически неопределимыми. Задача определения реакций связей, а затем внутренних силовых факторов в статически неопределимых стержневых системах называется раскрытием статической неопределимости. Порядок раскрытия статической неопределимости: 1) определяется степень статической неопределимости (число избыточных связей); 2) рассматривается статическая сторона задачи (составляются уравнения статического равновесия для заданной стержневой системы); 3) рассматривается деформационная сторона задачи (составляются уравнения совместности перемещений элементов стержневой системы); 4) рассматривается физическая сторона задачи (используя закон Гука, в уравнение совместности перемещений вводятся неизвестные реакции связей); 5) синтез: составляется система разрешающих уравнений и определяются неизвестные реакции связей. Основная трудность в решении таких задач заключается в особенностях составления уравнений совместности перемещений, соответствующих условиям деформирования заданной статически неопределимой стержневой системы. Разберем несколько типов решения подобных задач. Задача 1
Определить положение опасного сечения и подобрать параметр площади сечения А, если допускаемое напряжение на сжатие Степень статической неопределимости m = 1, поскольку две неизвестных реакции в защемлении, а уравнение статического равновесия одно. 1. Статическая сторона задачи
2. Деформационная сторона задачи Поскольку оба торца защемлены, то 3. Физическая сторона задачи По закону Гука На участке DC продольная сила постоянна, тогда
Методом сечений определим продольные силы на участках
Тогда
Подставляем полученные перемещения в уравнение совместности перемещений
получили второе уравнение для системы разрешающих уравнений. 4. Синтез: составляем систему разрешающих уравнений
После определения реакций связей стержень становится статически определимым. Для расчета на прочность построим эпюру продольных сил (рис. 3.4.5, а).
Для определения положения опасного сечения построим эпюру нормальных напряжений по длине стержня, сохраняя параметр площади А (рис. 3.4.5, б).
Наибольшее растягивающее напряжение действует на левом торце В
Из условия прочности
Наибольшие сжимающие напряжения достигаются на границе участков:
Следует оговориться, зону сжатия можно было не рассматривать, поскольку напряжения в зоне сжатия меньше растягивающих напряжений, а допускаемое на сжатие больше. Параметр площади А выбираем равным: А = 125 мм. Проверкой решения может служить перемещение сечения с относительно сечения В. Построим эпюру перемещений:
Полученное нулевое перемещение и является проверкой, поскольку правый торец защемлен, его перемещение должно быть нулевым. Для построения эпюры перемещения еще необходимо определить экстремум, т.е. перемещение точки, в которой
Построим эпюру перемещений (рис. 3.4.5, в).
Задача 2
Решение Количество связей, имеющихся в заданной стержневой системе, 4, количество уравнений, возможных для заданной стержневой системы 3, следовательно, степень статической неопределимости m = 1. 1. Статическая сторона задачи Рассечем стержни
Поскольку для расчета на прочность реакции в шарнире В не нужны, можно воспользоваться последним уравнением. После преобразования получим:
2. Деформационная сторона задачи Рассмотрим перемещения элементов стержневой системы.
Опустим из точки K перпендикуляр на новое положение стержня, получим отрезок K1K2 = Dl1 – удлинение стержня 1, СС1 – Dl2 – укорочение стержня 2. В уравнении совместности перемещений необходимо связать удлинения стержней. Из подобия треугольников DВСС1~DBKK1
3. Физическая сторона задачи По закону Гука
4. Синтез Система разрешающих уравнений
откуда N1 =0,43F, тогда N2 = 3,33×0,43F =1,42F.
Найдем напряжения в стержнях
Тогда запас стержневой системы
Задача 3 Вертикальная сила F действует на плоский узел с несимметрично расположенными стержнями (рис. 3.4.9). Вычислить усилия в стержнях, считая, что они выполнены из одного материала и имеют одинаковое поперечное сечение.
1. Статическая сторона задачи Рассечем стержни и рассмотрим равновесие узла В.
2. Деформационная сторона задачи
Обозначим j - угол, который отрезок ВВ1 составляет с вертикалью, тогда
откуда получим условие совместности перемещений.
Рассмотрим равенство
которое позволяет исключить угол (неизвестный) j из условий совместности деформаций.
разделим на cosj
откуда Рассмотрим равенство
разделим на cosj
По условию задачи b + g = a, кроме того подставим найденное значение tgj.
После громоздких, но несложных преобразований получили уравнение совместности перемещений, которое пока не содержит неизвестных усилий стержней. Введем неизвестные продольные силы в уравнение совместности перемещений. 3. Физическая сторона задачи По закону Гука
тогда получим
Составим систему разрешающих уравнений. 4. Синтез
Дальше решение легче проводить в числовых значениях коэффициентов:
или
Решая систему линейных уравнений (например, методом Гаусса), находим
Задача 4
Два уравнения статического равновесия
содержат 3 неизвестных усилия в стержнях: N1, N3, N4 стержневая система статически неопределима, со степенью статической неопределимости m = 1.
2. Деформационная сторона задачи Предположим, под действием силы F 1, 2, 3 стержни растягиваются; 4 и 5 стержни сжимаются.
Из треугольника ВВ1В2 получаем Из треугольника СС1С2 получаем Уравнение совместности перемещений получаем в виде
3. Физическая сторона задачи По закону Гука вводим продольные силы в уравнение совместности перемещений Подставим в уравнение совместности перемещений
Умножим на жесткость ЕА, разделим на l
4. Синтез Компонуем систему разрешающих уравнений
Складывая первое и второе уравнения, получаем
Умножаем второе уравнение на 3 и складываем с третьим
Для выявления опасного стержня найдем напряжения в стержнях
Максимальное напряжение возникает в третьем стержне
Допускаемая нагрузка:
Задача 5
Стержневая система статически неопределима, поскольку общее количество неизвестных реакций связей 4 (две реакции в шарнире о и продольные силы в стержнях), а возможных уравнений статического равновесия 3. 1. Статическая сторона задачи Рассечем стержни и составим уравнения статического равновесия (рис. 3.4.16):
2. Деформационная сторона задачи
ÐВ1ВВ2 = 30°, тогда тогда откуда, учитывая, что получаем
полученное уравнение является уравнением совместности перемещений. 3. Физическая сторона задачи По закону Гука вводим неизвестные усилия в стержнях в уравнение совместности перемещений
4. Синтез Поскольку с точки зрения расчета на прочность реакции в шарнире О не нужны, преобразуем уравнение момента и составим систему разрешающих уравнений
откуда откуда Для определения грузоподъемности, т.е. допускаемой нагрузки, определим опасный стержень
Большие напряжения возникают в первом стержне Максимально допускаемая нагрузка 53 кН.
|
Рис. 3.4.1
Рис. 3.4.2
.
, т.е. общее удлинение стержня = 0. Общее удлинение стержня равно сумме удлинений его частей 
, тогда 
является уравнением совместности перемещений.
, поскольку участок BD загружен распределенной нагрузкой.
.
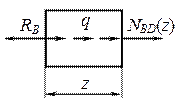Рис. 3.4.3
, 
, 
.
Рис. 3.4.4
, 
, 
.
,
.
, преобразуем:
или 
,
, отсюда 
, тогда
.
Рис. 3.4.5
- линейная зависимость, при 
, 
. Нанесем на эпюру (рис. 3.4.5, а). На втором участке 
.
; 
.
со стороны второго участка,
, сохраняет это значение на всем втором участке.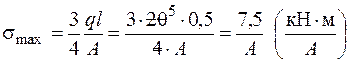
.
найдем параметр площади А:
, откуда 
мм2.
, тогда 
;
, откуда 
мм2.
– параболическая зависимость. Для построения эпюры найдем значения 
,
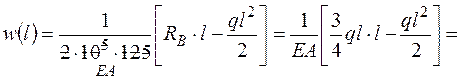
мм,
- линейная функция.
.
; определим положение стационарной точки: 
, откуда 
.
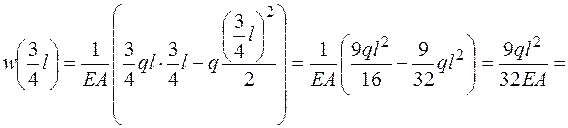
мм.
Рис. 3.4.6
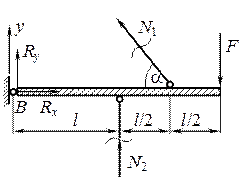Рис. 3.4.7
, 
, 
.
,
,
.
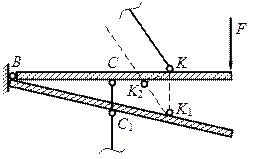Рис. 3.4.8
; 
, тогда 
; откуда
, получили уравнение совместности перемещений.
; 
. Подставим в уравнение совместности перемещений
или 10N1 = 3N2.
,
; 
,
МПа,
МПа.
.
Рис. 3.4.9
Рис. 3.4.10
Из двух уравнений невозможно определить три неизвестных силы, рассмотрим деформационную сторону задачи.
Рис. 3.4.11
- удлинение стержня 1, 
- удлинение стержня 2, ВВ4 – укорочение стержня 3. Отрезок ВВ1 является общей гипотенузой для всех треугольников, содержащих удлинения стержней.
,
,
,
.
,
,
,
,
,
.
,
,
,
.
,
;
;
.
; 
; 
;
; 
; 
,
,
.
; 
; 
.
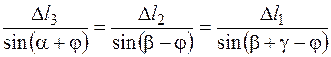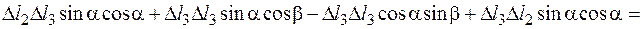
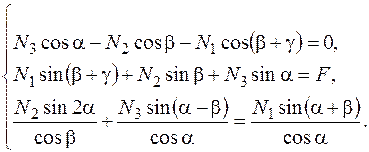
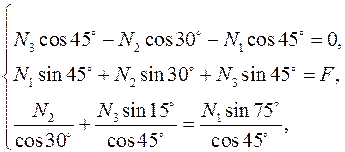
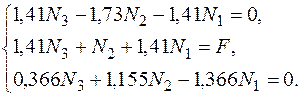
Рис. 3.4.12
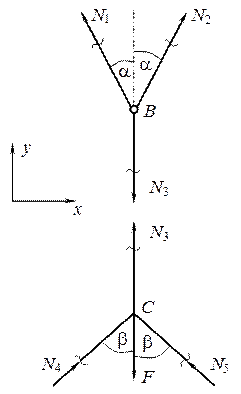Рис. 3.4.13
, откуда 
, 
. Равновесие узла С 
, откуда 
, 
.
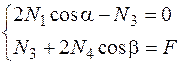
Рис. 3.4.14
; 
; 
.
.
.
.
; 
; 
.
.
; при заданных углах a = 30° и b = 45°,
или 
.
.
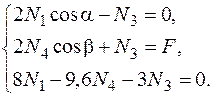
, учитывая величины углов, получим: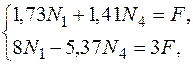
или
откуда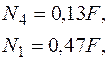 
.
; 
; 
.
по условию прочности 
,
, откуда 
.
кН.
Рис. 3.4.15
Рис. 3.4.16
, 
, 
Рис. 3.4.17
;
, 
;
, где 
, 
;
, 
,
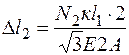или
,
; 
,
или 
, с учетом величины длин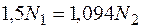 
.
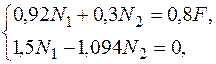
, тогда 
,
, 
.
; 
.
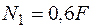, тогда по условию прочности 
, откуда 
кН.