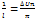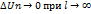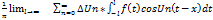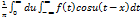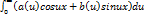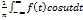ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Достаточные признаки разложимости в ряд Фурье. Разложение в ряд Фурье непериодической функции.
А)Точка х0 разрыва функции f(x) называют точкой разрыва первого рода, если существует конечные пределы справа и слева этой функции в данной точке.
ТЕОРЕМА 1 (Дирихле). Если f(x) периодическая с периодом 2π функция непрерывна или имеет конечное число точек разрыва 1-ого рода на отрезке [-π, π] и этот отрезок можно разбить на конечное число частей, в каждом из которых f(x) монотонна, то ряд Фурье относительно функции сходится к f(x) в точках непрерывности и к среднеарифметическому односторонних пределов в точках разрыва рода (Функция удовлетворяющая этим условиям называется кусочно-монотонной).
ТЕОРЕМА 2. Если f(x) периодическая функция с периодом , которая на отрезке [-π, π] вместе со своей производной непрерывна или имеет конечное число точек разрыва первого рода, то ряд Фурье функции f(x) в точках разрыва к среднему арифметическому односторонних пределов (Функция удовлетворяющая этой теореме называется кусочно-гладкой).
Б) Задача разложения непериодической функции в ряд Фурье в принципе не отличается от разложения в ряд Фурье периодической функции.
Допустим, функция f(x) задана на отрезке [a, b] и является на этом отрезке кусочно – монотонной. Рассмотрим произвольную периодическую кусочно – монотонную функцию f1(x) c периодом 2Т ³ ïb-aï, совпадающую с функцией f(x) на отрезке [a, b].
Таким образом, функция f(x) была дополнена. Теперь функция f1(x) разлагается в ряд Фурье. Сумма этого ряда во всех точках отрезка [a, b] совпадает с функцией f(x), т.е. можно считать, что функция f(x) разложена в ряд Фурье на отрезке [a, b].
Таким образом, если функция f(x) задана на отрезке, равном 2 π ничем не отличается от разложения в ряд периодической функции. Если же отрезок, на котором задана функция, меньше, чем 2 π, то функция продолжается на интервал (b, a + 2 π) так, что условия разложимости в ряд Фурье сохранялись.
Вообще говоря, в этом случае продолжение заданной функции на отрезок (интервал) длиной 2 π может быть произведено бесконечным количеством способов, поэтому суммы получившихся рядов будут различны, но они будут совпадать с заданной функцией f(x) на отрезке [a,b].
Ряд Фурье для четных и нечетных функций 1)
2)Если произведения двух четных и двух нечетных ,то получаем нечетную 3)Произведение четной и нечетной –нечетная Если f(x) четная периодическая функция с периодом 2π,удовлетворяет условиям разложимости в ряд Фурье, то можно записать: Аn= Где (n=0,1,2…) Bn= Таким образом для четной функции разложение в ряд Фурье выглядит так: F(x)= An= F(x)= Bn= Ряды Фурье для функции любого предела. Ряд Фурье для функции f(x) c периодом T=2L точек разрыва 1 рода на отрезке {-L;L} имеет вид: F(x)= A0= An= Bn= (n=1,2,…) f(x)= An= Четная (n=0,1,…) F(x)= Bn= (n=1,2…)
Интеграл Фурье Пусть функция f(x) на каждом отрезке (-L;L) где L-любое число, является кусочно-гладкой и кусочно-монотонной и f (x) абсолютно интегрирующаяся функция,тогда функция f(x) разлагается в ряд Фурье. F(x)= An= Bn= F(x)= dt* (t-x)dt Переходя к пределу L->
F(x)= An=
F(x)= F(x)= Двойной интеграл Фурье F(x)= A(u)= |




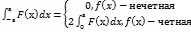
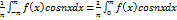
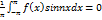
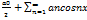
 =>>> четная функция
=>>> четная функция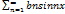
 =>>> нечетная
=>>> нечетная x+Bnsin
x+Bnsin 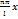
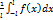
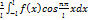
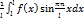
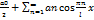
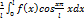 ->>>
->>>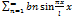
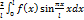

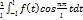
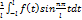 ,где (n=1,2..)
,где (n=1,2..)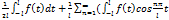

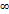
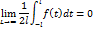
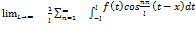
 un+1-un=
un+1-un= 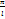 ,
,