 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Экзаменационный билет № 26
На первый взгляд может показаться, что закономерности заполнения микропор должны следовать теории капиллярной конденсации. Однако размеры микропор таковы, что в них происходит перекрытие полей поверхностных сил противоположных стенок пор, что значительно повышает энергию адсорбции и искажает профиль мениска конденсата в порах, соответствующий уравнению Кельвина, т. е. приводит к дополнительному всасыванию адсорбата, резкому увеличению адсорбционного потенциала. Особенности адсорбции на микропористых телах проявляются в их избирательном действии. Избирательность, или селективность, микропористых адсорбентов существенно выше, чем переходнопористых, благодаря тому, что большинство адсорбированных молекул взаимодействуют непосредственно с поверхностью адсорбента. В более крупных порах такое взаимодействие характерно только для первого слоя. В последующих же слоях взаимодействие не зависит от природы·, адсорбента, а определяется только природой адсорбата. Кроме этой особенности у микропор может проявляться так называемый ситовой эффект, заключающийся в том, что адсорбироваться могут только те молекулы, размеры которых меньше размеров микропор или равны им, в связи с чем все микропористые адсорбенты (не только цеолиты) называют молекулярными ситами. Переходя к количественным соотношениям теории объемного заполнения пор, необходимо отметить, что в ее основе лежат представления потенциальной теории Поляни, предложенной первоначально для описания полимолекулярной адсорбции, исходя из двух основных параметров: адсорбционного потенциала ε, адсорбционного объема V и двух положений:
Степень заполнения адсорбента можно· представить как отношение величины адсорбции А к максимальной адсорбции А0, или как отношение заполненного объема V к предельному объему адсорбционного пространства V0, приведенных к нормальным условиям (давлению и температуре).
Эти уравнения являются общими уравнениями теории объемного заполнения микропор. Заменив адсорбционный потенциал на его выражение через давление пара (ε = RTln(p/ps)) и прологарифмировав общее уравнение теории объемного заполнения микропор, получим:
Для большинства активных углей n=2, тогда полученное уравнение переходит в уравнение Дубинина— Радушкевича:
Построение прямой в координатах
Широкое признание и распространение получила теория устойчивости и коагуляции, учитывающая электростатическую составляющую расклинивающего давления (отталкивание) и его молекулярную составляющую. (притяжение). Эта теория удовлетворительно описывает закономерности поведения типично лиофобных дисперсных систем, для которых можно пренебречь адсорбционно-сольватным фактором устойчивости. В наиболее общем виде эта теория была разработана советскими учеными Б. В. Дерягиным и Л. Д. Ландау в 1937 — 1941 гг. и несколько позднее независимо от них голландскими учеными Фервеем и Овербеком; по первым буквам фамилий этих ученых теория названа теорией ДЛФО. Она рассматривает процесс взаимодействия частиц по отдельным стадиям — перекрывание их поверхностных слоев и возникновение расклинивающего давления, используя при этом понятие потенциального барьера, аналогичное энергии активации в химической кинетике. Расклинивающее давление возникает при сильном уменьшении толщины пленки (прослойки) в результате перекрывания (взаимодействия) поверхностных слоев (поверхностей разрыва). С расклинивающим давлением связана целая область явлений, включающая устойчивость дисперсных систем и пленок, полимолекулярную адсорбцию, набухание, массоперенос в дисперсных системах и др. В гетерогенных системах под пленкой понимают тонкую часть системы, находящуюся между двумя межфззными поверхностями. При уменьшении толщины пленки ограничивающие ее поверхностные слои начинают перекрываться (h<2σ), вследствие чего возникает давление, обусловленное взаимодействием как сближающихся фаз, так и межфазных слоев — расклинивающее давление. Таким образом, избыточные термодинамические функции тонкой пленки зависят от, ее толщины h.
Таким образом, расклинивающее давление можно рассматривать как разность гидростатических давлений в пленке и в окружающей пленку фазе или как приращение энергии Гиббса на данном расстоянии между поверхностными межфазными слоями, пересчитанное на единицу толщины пленки и отнесенное к единице площади перекрывания поверхностных слоев. Расклинивающее давление — суммарный параметр, учитывающий как силы отталкивания, так и силы притяжения, действующие в пленке. Общая энергия взаимодействия между двумя пластинами, приходящаяся на единицу их площади, равна
В теории ДЛФО (в ее классическом виде) принято, что давление отталкивания обусловлено только электростатическими силами, поэтому Давление Пэ обусловлено обычно стремлением системы к уменьшению поверхностной энергии, его природа связана с ван-дер-ваальсовыми силами. Для определения электростатической составляющей расклинивающего давления необходимо произвести интегрирование данного уравнения и ряд вычислений, который приведет к значению Пэ: а затем и к
Кривая 2 указывает на наличие достаточно высокого потенциального барьера и вторичного минимума. В системе, находящейся в таком состоянии, происходит быстрая флокуляция частиц (перед вторичным минимумом отсутствует потенциальный барьер) на расстояниях, соответствующих вторичному минимуму. Кривая 3 отвечает состоянию системы с высоким потенциальным барьером при отсутствии вторичного минимума или при его глубине, меньшей тепловой энергии (kбT). Вероятность образования агрегатов частиц в таких условиях очень мала, и дисперсные системы обладают большой агрегативной устойчивостью.
|




 или
или 
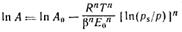

 дает возможности найти константы этого уравнения A0 и E. Объем микропор Vп рассчитывают по уравнениям
дает возможности найти константы этого уравнения A0 и E. Объем микропор Vп рассчитывают по уравнениям


 .
. ,
, .
. Различают три наиболее характерных вида потенциальных кривых, отвечающих определенным состояниям агрегативной устойчивости дисперсных систем. Кривая 1 соответствует такому состоянию дисперсной системы, при котором на любом расстоянии между частицами энергия притяжения преобладает над энергией отталкивания.
Различают три наиболее характерных вида потенциальных кривых, отвечающих определенным состояниям агрегативной устойчивости дисперсных систем. Кривая 1 соответствует такому состоянию дисперсной системы, при котором на любом расстоянии между частицами энергия притяжения преобладает над энергией отталкивания.