 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Экзаменационный билет № 16
Есть несколько определений поверхностного натяжения: 1. Поверхностное натяжение – работа образования новой поверхности в изотермическом процессе 2. Поверхностное натяжение – сила, действующая по периметру данной поверхности, отнесенная к единице длины. 3. Поверхностное натяжение – работа переноса молекул из объема тела на поверхность. 4. Термодинамическое определение поверхностного натяжения: Термодинамическое определение поверхностного натяжения вытекает из объединенного уравнения первого и второго начал термодинамики. Запишем его для гетерогенной системы относительно изменения внутренней энергии U:
При постоянных S, V, ni и q имеем:
т. е. поверхностное натяжение есть частная производная от внутренней энергии по площади поверхности раздела фаз при постоянных энтропии, объеме, числе молей компонентов и заряде. Так как объединенное уравнение первого и второго начал термодинамики может быть записано и относительно других термодинамических потенциалов, а именно энергии Гиббса G, энергии Гельмгольца F и энтальпии Я, то при соответствующих постоянных параметрах получим:
Таким образом, поверхностное натяжение есть частная производная от любого термодинамического потенциала по площади межфазной поверхности при постоянных соответствующих параметрах. Физический смысл поверхностного натяжения можно представить так: поверхностное натяжение на границе жидкости с газовой фазой – работа, расходуемая на обратимый разрыв столбика этой жидкости с поперечным сечением в 0,5 единицы площади, так как при разрыве образуется новая поверхность, равная единице площади. Чем сильнее межмолекулярные связи в данном теле, тем больше его поверхностное натяжение на границе с газовой фазой. В соответствии со вторым началом термодинамики избыточная энтропия равна
Учитывая, что Gs = σ, получим следующее выражение:
Из этого уравнения следует, что внутренняя энергия поверхности складывается из энергии Гиббса и теплоты образования поверхности. Для индивидуальных веществ теплота qs всегда положительна, так как при образовании поверхности теплота поглощается. Из уравнения объединенных первого и второго начала термодинамики при постоянстве всех параметров, кроме температуры, имеем:
Подставлям это выражение в полученные уравнения:
Это уравнение называется уравнением Гиббса — Гельмгольца. Оно связывает полную поверхностную энергию с энергией Гиббса (поверхностным натяжением). Из этого уравнения следует, что для определения полной поверхностной энергии необходимо знать зависимость поверхностного натяжения от температуры. Для индивидуальных веществ теплота qs всегда положительна, а это значит, что температурный коэффициент поверхностного натяжения отрицателен:
Таким образом, поверхностное натяжение индивидуальных веществ на границе с газом (воздухом) снижается с повышением температуры. Для большинства неполярных жидкостей эта зависимость линейная.
Структурно-механические свойства систем исследуют методами реологии — науки о деформациях и течении материальных систем. Реология изучает механические свойства систем по проявлению деформации под действием внешних напряжений. В коллоидной химии методы реологии используют для исследования структуры и описания вязкотекучих свойств дисперсных систем.
Идеально упругое тело Гука представляют в виде спиральной пружины. В соответствии с законом Гука деформация а упругом теле пропорциональна напряжению сдвига P:
После снятия нагрузки идеально упругое тело Гука мгновенно переходит в первоначальное состояние (форму).
Закон Ньютона можно сформулировать еще следующим образом: напряжение сдвига пропорционально скорости деформации (или скорость деформации пропорциональна напряжению сдвига):
Если напряжение достигнет предела текучести, то развиваемая деформация идеально пластического тела не имеет предела, и течение происходит с любой скоростью, т. е. при
Из рисунка видно, что свойства структурированных жндкообразных систем могут быть охарактеризованы тремя величинами вязкости: двумя ньютоновскими ηмакс для неразрушенной структуры, ηмин Для предельно разрушенной структуры и пластической вязкостью η* в промежуточной области, моделируемой уравнением Бингама. Наличие структуры и ее прочность, особенно в жидкообразных системах, можно оценивать не только пределом текучести, но и разностью ηмакс — ηмин.
|



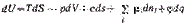







 В реологии механические свойства материалов представляют в виде реологических моделей, в основе которых лежат три основных идеальных закона, связывающих напряжение с деформацией. Им соответствуют три элементарные модели (элемента) идеализированных материалов, отвечающих основным реологическим характеристикам (упругость, пластичность, вязкость): идеально упругое тело Гука, идеально вязкое тело Ньютона (ньютоновская жидкость) и идеально пластическое тело Сен-Венана — Кулона.
В реологии механические свойства материалов представляют в виде реологических моделей, в основе которых лежат три основных идеальных закона, связывающих напряжение с деформацией. Им соответствуют три элементарные модели (элемента) идеализированных материалов, отвечающих основным реологическим характеристикам (упругость, пластичность, вязкость): идеально упругое тело Гука, идеально вязкое тело Ньютона (ньютоновская жидкость) и идеально пластическое тело Сен-Венана — Кулона.
 Идеально вязкое тело Ньютона изображают в виде поршня с отверстиями, помещенного в цилиндр с жидкостью. Идеально вязкая жидкость течет в соответствии с законом Ньютона. Согласно этому закону напряжение сдвига при ламинарном течении жидкости с вязкостью η пропорционально градиенту ее скорости du/dx:
Идеально вязкое тело Ньютона изображают в виде поршня с отверстиями, помещенного в цилиндр с жидкостью. Идеально вязкая жидкость течет в соответствии с законом Ньютона. Согласно этому закону напряжение сдвига при ламинарном течении жидкости с вязкостью η пропорционально градиенту ее скорости du/dx: 

 Моделью идеально пластического тела Сен-Венана — Кулона является находящееся на плоскости твердое тело, при движении которого трение постоянно и не зависит от нормальной (перпендикулярной поверхности) силы. В основе этой модели лежит закон внешнего (сухого) трения, в соответствии с которым деформация отсутствует, если напряжение сдвига меньше некоторой величины Рт, называемой пределом текучести, т. е. при
Моделью идеально пластического тела Сен-Венана — Кулона является находящееся на плоскости твердое тело, при движении которого трение постоянно и не зависит от нормальной (перпендикулярной поверхности) силы. В основе этой модели лежит закон внешнего (сухого) трения, в соответствии с которым деформация отсутствует, если напряжение сдвига меньше некоторой величины Рт, называемой пределом текучести, т. е. при  .
. .
. Кривые течения структурированных жидкообразных систем могут быть представлены в координатах вязкость — напряжение сдвига.
Кривые течения структурированных жидкообразных систем могут быть представлены в координатах вязкость — напряжение сдвига.