 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Экзаменационный билет № 10
Экзаменационный билет № 1 1. Предмет коллоидной химии. Признаки объектов коллоидной химии. Поверхностная энергия и поверхностные явления. Количественные характеристики дисперсности. Классификация дисперсных систем. Коллоидная химия и химическая технология. Коллоидная химия – физическая химия поверхностных явлений и дисперсных систем. Признаки коллоидных систем: 1. Гетерогенность 2. Дисперсность. Гетерогенность количественно определяется поверхностным натяжением — величиной, характеризующей энергию единицы поверхности и являющейся фактором интенсивности. Поверхностное натяжение определяет как бы степень гетерогенности, резкость перехода от одной фазы к другой, различие между соприкасающимися фазами. Чем сильнее выражена гетерогенность и чем более резко различаются по природе сопряженные фазы, тем больше поверхностное натяжение. Отсутствие гетерогенности равнозначно отсутствию поверхностного натяжения. Гетерогенным системам присуща поверхностная энергия: G = σ·s. Второй признак — дисперсность. Дисперсность – величина, обратная поперечному размеру частиц: D=1/а. Системы с малой дисперсностью (менее 103 см-1) не принято рассматривать как коллоидные. Широко применяется и третья характеристика раздробленности — удельная поверхность Sуд, определяемая отношением площади межфазной поверхности к объему тела s/V, Все три характеристики раздробленности связаны между собой: с уменьшением размера а увеличиваются дисперсность D и удельная поверхность Sуд. Классификация по кинетическим свойствам: 1. Свободнодисперсные системы (частицы не связаны друг с другом, свободное броуновское движение) 2. Связнодисперсные системы (частицы образуют пространственную решетку) Классификация по размеру частиц: 1. Ультрамикрогетерогенные системы (золи): r = 1 – 100 нм 2. Микрогетерогенные системы (суспензии): r = 100 – 104 нм 3. Грубодисперсные системы: r = 0,1 – 10 мкм Коллоидные явления широко распространены в химической технологии. Практически нет такого химического производства, которое бы не осуществлялось с участием поверхностных явлений и дисперсных систем. Измельчение сырья и промежуточных продуктов, обогащение, в том числе флотация, сгущение, отстаивание и фильтрация, конденсация, кристаллизация и вообще процессы образования новых фаз, брикетирование, спекание, гранулирование — все эти процессы протекают в дисперсных системах, и в них большую роль играют такие коллоидно-химические явления, как смачивание, капиллярность, адсорбция, седиментация, коагуляция. Большое распространение в химической технологии получили адсорбенты и катализаторы, которые представляют собой дисперсные системы с твердой дисперсионной средой. Адсорбция имеет самостоятельное значение для очистки и разделения веществ, извлечения ценных компонентов, хроматографии и др. Как правило, все гетерогенные процессы в химической технологии для увеличения их скорости проводят при максимальной поверхности контакта фаз. Это значит, что системы в реакционных аппаратах находятся в состоянии суспензий, паст, пульп, эмульсий, пен, порошков, туманов, пылей. Несмотря на то что толщина поверхностных слоев не превышает несколько молекул, их роль не менее важна, чем объемных фаз, например, в процессах массопередачи (адсорбция, экстракция, сушка, испарение и др.), термоэлектронной эмиссии, смазочном действии, адгезии. 2. Общие представления о теориях строения ДЭС. Уравнение Пуассона-Больцмана для диффузной части ДЭС и его решение для случая слабозаряженных поверхностей. Уравнение Гуи-Чепмена. Все электрические свойства межфазных поверхностей и явления, протекающие на них, обусловлены наличием двойного электрического слоя на границе раздела фаз. Количественные связи между параметрами двойного электрического слоя определяются его строением. Первые предположения об образовании двойного электрического слоя были сделаны Квинке. Строение двойного электрического слоя впервые было представлено Гельмгольцем и Перреном по аналогии со строением плоского конденсатора. Согласно их представлениям, на границе соприкасающихся фаз заряды располагаются в виде двух рядов разноименных ионов: ряд потенциалопредвляющих ионов на расстоянии, равном их радиусу в несольватированном состоянии, и прилегающий к нему ряд противоионов. Толщина электрического слоя близка к молекулярным размерам или размерам сольватированных ионов. Потенциал слоя снижается в пределах его толщины линейно до нуля. Поверхностный заряд qs определяется в соответствии с теорией плоского конденсатора уравнением:
Вполне естественно, что подобное строение двойного слоя возможно при отсутствии теплового движения ионов. В реальных же условиях распределение зарядов на границе раздела фаз в первом приближении определяется соотношением сил электростатического притяжения ионов, зависящего от электрического потенциала φ0 и теплового движения ионов, стремящихся равномерно распределиться во всем объеме жидкой или газообразной фазы. К такому выводу независимо друг от друга пришли Гуи и Чепмен. Они предположили, что двойной электрический слой имеет диффузное (размытое) строение и все противоионы находятся в диффузной его части — в диффузном слое. Поскольку протяженность диффузного слоя определяется кинетической энергией ионов, то в области температур, близких к абсолютному нулю, все противоионы будут находиться в непосредственной близости к потенциалопределяющим ионам.
Одна часть примыкает непосредственно к межфазной поверхности и образует адсорбционный слои (слой Гельмгсиьца) толщиной δ, которая равна радиусу гидратированных ионов, его составляющих. Другая часть противононов находится в диффузной части — диффузный слой (слой Гуи) с потенциалом φδ, толщина λ которой может быть значительной и зависит от свойств и состава системы. Потенциал в диффузной части двойного электрического слоя не может зависеть линейно от расстояния, так как ионы в нем распределены неравномерно. В соответствии с принятыми представлениями потенциал в слое Гельмгольца при увеличении расстояния от слоя потенциалопределяющих ионов снижается до потенциала диффузного слоя линейно, а затем, как будет показано, по экспоненте. Теория Штерна учитывает также специфическую (некулоновскую, химическую) составляющую адсорбции ионов на поверхности раздела фаз, которая существенным образом может влиять на изменение потенциала. Уравнение Пуассона — Больцмана:
Это уравнение после двойного интегрирования дает соотношение, выражающее закон изменения поверхностного потенциала от расстояния в диффузной части двойного электрического слоя и от свойств раствора. Чтобы в полной мере представлять возможности этого соотношения, лежащего в основе теории двойного электрического слоя, необходимо учитывать основные допущения и предположения, принятые Гуи и Чепменом при его выводе: двойной электрический слой является плоским, диэлектрическая проницаемость не зависит от расстояния х, ионы представляют собой точечные заряды (т. е. не имеют объема), при переводе противоионов из объема раствора в двойной электрический слой совершается работа только против электростатических сил. Обычно уравнение Пуассона — Больцмана решают применительно к конкретным граничным условиям. Ниже приводится его решение при условии малости потенциала диффузного слоя (φδ<<25 мВ). Обозначим экспоненциальный показатель у фактора Больцмана через у. При малых значениях φ и соответственно y<<1 фактор Больцмана можно разложить в ряд Маклорена:
Если ограничиться двумя первыми членами ряда, то уравнение для объемной плотности заряда после этих преобразований примет вид:
Первый член правой части этого уравнения равен нулю. так как он включает сумму зарядов в объеме раствора, которая по условиям электронейтральности равна нулю, и поэтому окончательно имеем:
После такого преобразования уравнение Пуассона — Больцмана принимает следующую форму:
Выражение æ2 перед φх включает постоянные, характеризующие свойства раствора, поэтому можно считать, что они не изменяются с расстоянием от поверхности:
Окончательно имеем: Если расстояние х отсчитывать от начала диффузной части двойного электрического слоя, то Последние уравнения называются уравнениями Гуи-Чепмена, из них следует, что потенциал в области диффузного слоя в зависимости от расстояния уменьшается по экспоненте. 3. Рассчитайте удельную поверхность адсорбента по изотерме адсорбции азота, используя уравнение БЭТ. Площадь, занимаемая молекулой азота в плотном монослое, составляет 16·10-20 м2.
Экзаменационный билет № 2
Есть несколько определений поверхностного натяжения: 1. Поверхностное натяжение – работа образования новой поверхности в изотермическом процессе 2. Поверхностное натяжение – сила, действующая по периметру данной поверхности, отнесенная к единице длины. 3. Поверхностное натяжение – работа переноса молекул из объема тела на поверхность. 4. Термодинамическое определение поверхностного натяжения: Термодинамическое определение поверхностного натяжения вытекает из объединенного уравнения первого и второго начал термодинамики. Запишем его для гетерогенной системы относительно изменения внутренней энергии U:
При постоянных S, V, ni и q имеем:
т. е. поверхностное натяжение есть частная производная от внутренней энергии по площади поверхности раздела фаз при постоянных энтропии, объеме, числе молей компонентов и заряде. Так как объединенное уравнение первого и второго начал термодинамики может быть записано и относительно других термодинамических потенциалов, а именно энергии Гиббса G, энергии Гельмгольца F и энтальпии Я, то при соответствующих постоянных параметрах получим:
Таким образом, поверхностное натяжение есть частная производная от любого термодинамического потенциала по площади межфазной поверхности при постоянных соответствующих параметрах. Физический смысл поверхностного натяжения можно представить так: поверхностное натяжение на границе жидкости с газовой фазой – работа, расходуемая на обратимый разрыв столбика этой жидкости с поперечным сечением в 0,5 единицы площади, так как при разрыве образуется новая поверхность, равная единице площади. Чем сильнее межмолекулярные связи в данном теле, тем больше его поверхностное натяжение на границе с газовой фазой. В соответствии со вторым началом термодинамики избыточная энтропия равна
Учитывая, что Gs = σ, получим следующее выражение:
Из этого уравнения следует, что внутренняя энергия поверхности складывается из энергии Гиббса и теплоты образования поверхности. Для индивидуальных веществ теплота qs всегда положительна, так как при образовании поверхности теплота поглощается. Из уравнения объединенных первого и второго начала термодинамики при постоянстве всех параметров, кроме температуры, имеем:
Подставлям это выражение в полученные уравнения:
Это уравнение называется уравнением Гиббса — Гельмгольца. Оно связывает полную поверхностную энергию с энергией Гиббса (поверхностным натяжением). Из этого уравнения следует, что для определения полной поверхностной энергии необходимо знать зависимость поверхностного натяжения от температуры. Для индивидуальных веществ теплота qs всегда положительна, а это значит, что температурный коэффициент поверхностного натяжения отрицателен:
Таким образом, поверхностное натяжение индивидуальных веществ на границе с газом (воздухом) снижается с повышением температуры. Для большинства неполярных жидкостей эта зависимость линейная.
Различают три возможных механизма образования двойного электрического слоя: 1. Двойной электрический слой образуется в результате перехода ионов или электронов из одной фазы в другую (поверхностная ионизация). Например, с поверхности металла в газовую фазу переходят электроны, создавая электронное облако со стороны газовой фазы. 2. Образование двойного электрического слоя происходит в результате адсорбции. Двойной электрический слой может образоваться при избирательной адсорбции в межфазном слое ионов электролитов, не входящих в состав веществ, образующих фазы, т. е. в результате адсорбции примесей. 3. Если вещества, составляющие фазы системы, не способны обмениваться зарядами, то двойной электрический слой может образоваться благодаря ориентированию полярных молекул сопряженных фаз в результате их взаимодействия. Из объединенных первого и второго начал термодинамики, а также полного дифференциала энергии Гиббса выводится первое уравнение Липпмана, связывающее электрический потенциал с поверхностным натяжением:
Если знаки потенциала и заряда совпадают, то поверхностное натяжение снижается с ростом потенциала. Если же их знаки противоположны, то увеличение потенциала ведет к росту поверхностного натяжения. Эти зависимости тем сильнее,чем больше абсолютное значение плотности заряда. При минимальной плотности заряда поверхностное натяжение слабо зависит от потенциала. Дифференциальная емкость двойного электрического слоя, как н любого конденсатора, определяется соотношением:
После дифференцирования первого уравнения Липмана по φ и подстановки в него данного соотношения получим второе уравнение Липпмана:
Это уравнение показывает возможность определения емкости двойного электрического слоя, если известна зависимость σ от φ.
Это уравнение называют уравнением электрокапиллярной кривой. Из него следует, что поверхностное натяжение при условии постоянства емкости двойного электрического слоя изменяется в соответствии с уравнением параболы.
Вершина параболы отвечает максимальному поверхностному натяжению σмакс. Парабола симметрична, что по физическому смыслу означает равное сродство катионов и анионов, выступающих в роли противоионов, к поверхности, имеющей соответственно отрицательный и положительный потенциал. Уменьшение положительного потенциала, как и отрицательного, ведет к увеличению поверхностного натяжения. Однако в реальных системах емкость двойного электрического слоя несколько изменяется с изменением потенциала, и поэтому экспериментальные электрокапиллярные кривые обычно не являются симметричными. Вершина параболы соответствует точке нулевого заряда. В этой точке поверхностное натяжение не зависит от потенциала, так как производная dσ/dφ равна нулю, т. е. поверхностный слой имеет нулевой заряд, что означает отсутствие двойного электрического слоя. Потенциал же поверхности в этой, точке не равен нулю.
Экзаменационный билет № 3
Для описания термодинамики поверхностных явлений применяют два метода: метод избыточных величин Гиббса и метод «слоя конечной толщины».
Характеристика величины адсорбции определяющася избытком вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же объеме фазы, также отнесенным к единице площади поверхности или единице массы адсорбента, называется гиббсовской адсорбцией и обозначается буквой гамма Г (метод избыточных величин Гиббса). Объединенное уравнение первого и второго начал термодинамики для внутренней энергии поверхности с учетом поверхностной и химической энергии имеет вид (объем поверхностного слоя равен нулю)
Так как внутренняя энергия поверхности пропорциональна экстенсивным величинам, то и ее полный дифференциал от тех же переменных запишется следующим образом:
Подставляя значение dU, получим:
Разделив полученное уравнение на площадь поверхности, получим:
Данное уравнение называют фундаментальным адсорбционным уравнением Гиббса. Для адсорбции одного конкретного вещества при постоянных химических потенциалах других веществ полученное уравнение можно записать относительно частной производной для данного компонента:
Принимая во внимание, что Для гиббсовской адсорбции это выражение принимает вид
Общее определение поверхностной активности дается соотношением:
которое справедливо как для неэлектролитов, так и для электролитов. Поверхностная активность, как и гиббсовская адсорбция, может быть положительной и отрицательной. Абсолютное значение и ее знак зависят от природы как адсорбируемого вещества, так и среды (растворителя). Если с увеличением концентрации вещества поверхностное натяжение на границе раздела фаз понижается, то такое вещество называют поверхностно-активным. Для таких веществ Вещества, повышающие поверхностное натяжение на границе раздела фаз с увеличением концентрации, называют поверхностно-инактивными. Для них
Одна часть примыкает непосредственно к межфазной поверхности и образует адсорбционный слои (слой Гельмгсиьца) толщиной δ, которая равна радиусу гидратированных ионов, его составляющих. Другая часть противононов находится в диффузной части — диффузный слой (слой Гуи) с потенциалом φδ, толщина λ которой может быть значительной и зависит от свойств и состава системы. Потенциал в диффузной части двойного электрического слоя не может зависеть линейно от расстояния, так как ионы в нем распределены неравномерно. В соответствии с принятыми представлениями потенциал в слое Гельмгольца при увеличении расстояния от слоя потенциалопределяющих ионов снижается до потенциала диффузного слоя линейно, а затем, как будет показано, по экспоненте. Теория Штерна учитывает также специфическую (некулоновскую, химическую) составляющую адсорбции ионов на поверхности раздела фаз, которая существенным образом может влиять на изменение потенциала. Пренебрежение размерами ионов приводит к тому, что не принимается во внимание толщина адсорбционною слон, и это, в свою очередь, вызывает большие погрешности при расчете параметров двойного электрического слоя. Кроме того, теория Гуи — Чепмена рассматривая только влияние концентрации и заряда ионов электролитов на изменение потенциала, не объясняет различного действия ионов разной природы, связанного со специфической адсорбцией их на межфазной поверхности. Штерн предложил рассматривать слой противоионов состоящим из двух частей: внутренней (плотный слой Гельмгольца) и внешней (диффузный слой). Таким образом, теорию Гуи — Чепмена можно использовать для описания только строения внешней части слоя, где можно пренебречь адсорбционными силами и размерами ионов. Внутреннюю (плотную) часть Штерн представил как адсорбционный моноионный слой, в котором противоионы примыкают к поверхности благодаря электростатическим силам и специфическому взаимодействию. Введенный Штерном потенциал φδ часто называют штерновским. В плотной части двойного электрического слоя потенциал уменьшается линейно от φ0 до φδ. Принимая текущими переменными φ и х вместо φδ и δ, получим: Штерн попытался учесть влияние специфической адсорбции ионов на электрический потенциал, обусловленный действием ковалентных сил дополнительно к электростатическим силам. Так как радиус действия сил такой адсорбции соизмерим с размером ионов, это дает основание учитывать копалентные силы только для ионов, входящих в плотный слой Гельмгольца. Как видно из рисунка, плотность поверхностного заряда противоионов можно разделить на две части: плотность заряда qГ, обусловленного моноионным слоем, представляющим собой слой Гельмгольца, и плотность заряда qδ диффузного слоя Гуи. Общая поверхностная плотность заряда двойного электрического слоя равна сумме поверхностных плотностей зарядов плотного и диффузного слоев с обратным знаком: По Штерну, заряд слоя Гельмгольца складывается из заряда ионов, адсорбированых как за счет электростатического адсорбционного потенциала Fzφ, так и за счет потенциала специфической адсорбции Ф. Было предположено, что поверхность имеет определенное число адсорбционных центров, каждый из которых взаимодействует с одним противоионом. Пример образования ДЭС:
Сильно адсорбирующиеся ионы в плотном слое иногда способны не только полностью скомпенсировать поверхностный потенциал, но и создать избыточный заряд со знаком заряда противоионов. Это явление называется перезарядкой. Перезарядка приводит к смене противоионов в диффузном слое на ионы с зарядом другого знака. На рисунке видно, что при перезарядке поверхностный потенциал φ0 и потенциал диффузного слоя φδ имеют разные знаки. На формирование двойного электрического слоя существенное влияние оказывает природа поверхности конденсированной фазы, наличие определенных ионов в растворе, их концентрация. Рассмотрим систему водный раствор — поверхность иодида серебра. При избытке в растворе ионов серебра, например при добавлении нитрата серебра, эти ионы являются потенцналопределяюшими. В роли противоионов выступают нитрат-ионы, часть которых находится в плотном слое, а другая часть — в диффузном слое. Для такой системы формулу двойного электрического слоя можно записать следующим образом: В дисперсных системах двойной электрический слой возникает на поверхности частиц. Частицу дисперсной фазы в гетерогенно-дисперсной системе вместе с двойным электрическим слоем называют мицеллой. Строение мицеллы можно показать той же формулой, что и строение двойного электрического слоя. Внутреннюю часть мицеллы составляет агрегат основного вещества. На поверхности агрегата расположены потенциалопре-деляющие ионы. Агрегат вместе с потенциалопределяющими ионами составляет ядро мицеллы. Ядро с противоионами плотной части двойного электрического слоя образуют гранулу. Гранулу окружают противоионы диффузного слоя. Мицелла в отличие от гранулы электронейтральна. {(AgI)mnAg+|(n-x)NO3-}xNO3-
Экзаменационный билет № 4
Адгезия, смачивание и растекание относятся к межфазным взаимодействиям, которые происходят между конденсированными фазами. Межфазное взаимодействие, или взаимодействие между приведенными в контакт поверхностями конденсированных тел разной природы, называют адгезией (прилипанием). Работа адгезии Wа, характеризующая прочность адгезионной связи, определяется работой обратимого разрыва адгезионной связи, отнесенной к единице площади. Ома измеряется в тех же единицах, что и поверхностное натяжение (Дж/м2). Полная работа адгезии, приходящаяся на всю площадь контакта тел s, равна
Для начального и конечного состояний системы имеем Изменение энергии Гиббса системы в процесс адгезии равно или
Это уравнение Дюпре. Оно отражает закон сохранения энергии при адгезии. Условие растворения: Смачивание— это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом). Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания), или просто краевым углом (углом смачивания).
Так как поверхностное натяжение можно рассматривать как энергию, приходящуюся на единицу площади, или как силу, действующую на единицу длины, то все рассмотренные составляющие поверхностной энергии можно выразить с помощью векторов сил. При равновесии между ними соблюдается следующее соотношение:
Полученное соотношение называется законом Юнга. Чем меньше угол Θ и соответственно больше cos θ, тем лучше смачивается поверхность. При остром угле Θ, т. е. при cos θ>0, поверхность считают хорошо смачиваемой данной жидкостью. Если угол θ тупой, т. е. соs θ<0, то по отношению к данной жидкости поверхность смачивается плохо (часто говорят «не смачивается»). Уравнение Дюпре самостоятельно почти не используется для расчета работы адгезии из-за трудности определения поверхностного натяжения твердых тел на границе с газом (воздухом) и жидкостью. Удобную для расчета этой величины форму имеет соотношение, получаемое в результате сочетания уравнения Дюпре с законом Юнга Если разность
Это уравнение называют уравнением Дюпре-Юнга; оно связывает работу адгезии с краевым углом и позволяет рассчитать работу адгезии, если известны поверхностное натяжение жидкости и краевой угол. Обе эти величины можно сравнительно легко определить экспериментально. Введение ПАВ уменьшает работу когезии (поверхностное натяжение) жидкости а значит, как следует из уравнения Дюпре-Юнга, увеличивает смачивание. Лучше смачивает та жидкость, которая имеет меньшее поверхностное натяжение или работу когезии.
Протекание электрокинетических явлений в дисперсных системах возможно при наличии на границе раздела фаз двойного электрического слоя, имеющего диффузное строение. При относительном перемещении фаз независимо от причин, его вызвавших, происходит разрыв двойного электрического слоя по плоскости скольжения. Потенциал, возникающий на плоскости скольжения при отрыве части диффузного слоя, называется электрокинетическим потенциалом или ζ (дзета)-потенциалом. Для получения наиболее простого уравнения, связывающего скорость относительного движения фаз с параметрами дисперсионной среды (вязкость, диэлектрическая проницаемость), двойного электрического слоя (ζ-потенциал) и внешнего электрического поля (напряженность), необходимо задаться некоторыми ограничениями: 1) толщина двойного электрического слоя значительно меньше радиуса пор, капилляров твердой фазы (радиуса кривизны поверхности твердой фазы); 2) слой жидкости, непосредственно прилегающий к твердой фазе, неподвижен, движение жидкости в порах твердой фазы ламинарное и подчиняется законам гидродинамики; 3) распределение зарядов в двойном электрическом слое не зависит от приложенной разности потенциалов; 4) твердая фаза является диэлектриком, а жидкость проводит электрический ток. Электрическая сила, действующая на слой жидкости dх (в расчете на единицу площади поверхности), равна
Сила трения и ее дифференциал, приходящиеся на единицу площади (согласно закону Ньютона), составляют:
При установившемся движении (в стационарном состоянии) dFэл = dFтр:
После интегрирования, окончательно получим следующее выражение для постоянной линейной скорости жидкости относительно мембраны: Это уравнение носит название уравнения Гельмгольца — Смолуховского. Уравнение Гельмгольца — Смолуховского чаще записывают относительно ζ-потенциала: Это дифференциальное уравнение справедливо как для электроосмоса, так и для электрофореза, поскольку оно было выведено из баланса движущих сил процесса — электрической силы и силы трения. Отличие состоит только в выбранной системе координат. Несовпадение экспериментальных и теоретических значений электрофоретической подвижности определяется в основном двумя эффектами, неучтенными теорией Гельмгольца — Смолуховского: релаксационным эффектом и электрофоретическим торможением. Релаксационный эффект проявляется в нарушении симметрии диффузного слоя вокруг частицы при относительном движении фаз в противоположные стороны. Возникает внутреннее электрическое поле (диполь), направленное против внешнего поля. Для восстановления равновесного состояния системы требуется некоторое время, называемое временем релаксации. Электрофоретическое торможение обусловлено сопротивлением движению частицы обратным потоком противоионов, который увлекает за собой жидкость. Вследствие этого электрофоретическая скорость уменьшается.
Экзаменационный билет № 5
Дисперсность является самостоятельным и полноправным термодинамическим параметром системы, а для дисперсных систем правило фаз Гиббса принимает следующий вид:
F – количество степеней свободы, К – количество компонентов, Ф – количество фаз.
Кривизна вызывает изменение площади и положения межфазной поверхности, что можно выразить приращением поверхностной энергии σds. Кроме того, изменяются объемы фаз V1 и V2 на dV1 и dV2. При условии постоянства объема всей системы dV1 = - dV2. Изменение объемов вызывает соответствующие изменения энергий фаз 1 и 2 на p1dV1 и p2dV2 (где p1 и р2 — давления внутри фаз). Соотношение между поверхностной энергией и «объемной» можно записать с помощью обобщенного уравнения первого и второго начал термодинамики относительно энергии Гельмгольца F при T=const: При равновесии между фазами ΔF = 0, тогда Это уравнение называется уравнением Лапласа. Для сферической поверхности Капиллярные явления наблюдаются в содержащих жидкость узких сосудах (капилляры, капиллярно-пористые тела), у которых расстояние между стенками соизмеримо с радиусом кривизны поверхности жидкости. Кривизна возникает в результате взаимодействия жидкости со стенками сосуда (адгезия, смачивание). Специфика поведения жидкости в капиллярных сосудах зависит от того, смачивает или не смачивает жидкость стенки сосуда, точнее, от значения краевого угла.
Чтобы высоту капиллярного поднятия связать с характеристикой смачивания, радиус мениска необходимо выразить через угол смачивания θ и радиус капилляра r0. На рисунке показан мениск жидкости в капилляре. Видно, что r0 = r·соsθ, тогда высоту капиллярного поднятия можно представить в виде формулы Жюрена:
Характерным общим свойством суспензий, порошков, эмульсий и аэрозолей, особенно если они разбавлены, является склонность к оседанию или всплыванию частиц дисперсной фазы. Оседание частиц дисперсной фазы называется седиментацией, а всплывание частиц — обратной седиментацией. На каждую частицу в системе действует сила тяжести (гравитационная сила) и подъемная сила Архимеда: Эти силы постоянны и направлены в разные стороны, равнодействующая сила, вызывающая седиментацию, равна: Так как седиментация протекает в определенной среде, то при ламинарном движении частицы возникает сопротивление — сила трения, пропорциональная скорости движения частицы: Таким образом, сила, действующая на частицу, во время движения, равна: C ростом скорости при достаточно большом коэффициенте трения наступает момент, когда сила трения достигает силы, вызывающей седиментацию, и таким образом движущая сила F оказывается равной нулю.
Выражение для силы трения, возникающей при движении сферических частиц, можно представить в виде закона Стокса: Подставляя ее в полученное уравнение и выражая объем частицы через ее радиус, получим:
1) Закон Стокса справедлив, если частицы дисперсной фазы осаждаются независимо друг от друга, что может быть только в разбавленных системах. 2) Обычно частицы в дисперсных системах и твердой дисперсной фазой имеют неправильную форму. При свободном оседании частица несферической формы ориентируется в направлении движения таким образом, чтобы создавалось максимальное сопротивление движению, что уменьшает скорость осаждения. 3) Закон Стокса может не соблюдаться и при турбулентном режиме осаждения частиц. 4) Закон Стокса предполагает наличие внутреннего трения, или вязкого трения, когда граница (поверхность) движения частицы относительно среды находится внутри дисперсионной среды, вязкость которой определяет коэффициент трения. Если межфазное взаимодействие мало, граница (поверхность) движения частицы относительно среды может совпадать с поверхностью раздела фаз и трение оказывается внешним. Это приводит к возникновению скольжения, ускоряющему движение частицы. 5) Применимость закона Стокса ограничивается также дисперсностью частиц. Большие частицы (>100 мкм) могут двигаться ускоренно, очень малые частицы — ультрамикрпгетерогенные (<0,1 мкм) осаждаются настолько медленно, что следить за такой седиментацией практически невозможно. Принцип седиментационного метода анализа дисперсности состоит в измерении скорости осаждения частиц, обычно в жидкой среде. По скорости осаждения с помощью соответствующих уравнений рассчитывают размеры частиц. Метод позволяет определить распределение частиц по размерам и соответственно подсчитать их удельную поверхность.
Имеются графические и аналитические методы расчета кривой седиментации. Реальная кривая седиментации полидисперсной системы обычно получается плавной и ей отвечает множество бесконечно малых участков, касательные в каждой точке этой кривой отражают седиментацию данной бесконечно малой фракции. Результаты седиментациоиного анализа дисперсности полиднсперсных систем представляют также в виде кривых распределения частиц по размерам, характеризующих степень полиднсперсности системы. Кривая распределения является наглядной и удобной характеристикой полидисперсности системы, по которой легко определить содержание различных фракций. Ее строят подобно кривой распределения пор по размерам. Обычно сначала получают интегральную кривую распределения, проводят ее выравнивание с учетом точности получаемых средних значений радиусов частиц фракций и затем по ней строят дифференциальную кривую распределения. Иногда дифференциальную кривую строят сразу. На оси абсцисс откладывают значения радиусов; на ось ординат наносят отношение приращения массовых долей к разности радиусов частиц соседних фракций Δx/Δri. Построив на графике отдельные прямоугольники для каждой фракции (гистограмму) и соединив плавной кривой середины их верхних сторон, получают дифференциальную кривую распределения частиц полидисперсной системы по размерам.
Экзаменационный билет № 6
Термодинамическая реакционная способность характеризует способность вещества переходить в какое-либо иное состояние, например, переходить в другую фазу, вступать в химическую реакцию. Она указывает на удаленность данного состояния вещества или системы компонентов от равновесного состояния при определенных условиях. Термодинамическая реакционная способность определяется химическим сродством, которое можно выразить изменением энергии Гиббса или разностью химических потенциалов. Реакционная способность зависит от степени дисперсности вещества, изменение которой может приводить к сдвигу фазового или химического равновесия. Соответствующее приращение энергии Гиббса dGд (благодаря изменению дисперсности) можно представить в виде объединенного уравнения первого и второго начал термодинамики:
Для индивидуального вещества V=Vм и при Т=const имеем: Подставляя в это уравнение соотношение Лапласа, получим: для сферической кривизны: Если рассматривается переход вещества из конденсированной фазы в газообразную, то энергию Гиббса можно выразить через давление пара, приняв его за идеальный. Дополнительное изменение энергии Гиббса, связанное с изменением дисперсности, составляет: Подставляя данное выражение, получим:
Полученное соотношение называется уравнением Кельвина (уравнение капиллярной конденсации). Для неэлектролитов его можно записать следующим образом:
Из этого уравнения видно, что с увеличением дисперсности растворимость растет, или химический потенциал частиц дисперсной системы больше, чем у крупной частицы, на величину 2σV/r. Степень дисперсности может влиять также на равновесие химической реакции:
С увеличением дисперсности повышается активность компонентов, а в соответствии с этим изменяется константа химического равновесия в ту или другую сторону, в зависимости от степени дисперсности исходных веществ и продуктов реакции. С изменением дисперсности веществ изменяется температура фазового перехода. Количественная взаимосвязь между температурой фазового перехода и дисперсностью вытекает из термодинамических соотношений. Для фазового перехода: Для сферических частиц: Видно, что с уменьшением размера частиц и температуры плавления и испарения вещества уменьшаются (Hф.п.>0).
Основой доказательства теплового молекулярного движения в телах явилось обнаруженное английским ботаником Робертом Броуном в 1827 г. с помощью микроскопа непрерывное движете очень мелких частичек — спор папоротника (цветочной пыльцы), взвешенных в воде. Более крупные частицы находились в состоянии постоянного колебания около положения равновесия. Колебания и перемещения частиц ускорялись с уменьшением их размера и повышением температуры и не были связаны с какими-либо внешними механическими воздействиями. Теоретически обоснованная интерпретация броуновского движения — участие частиц дисперсной фазы ультрамикрогетерогенных систем в тепловом движении — была дана независимо друг от друга Эйнштейнии (1905 г.) и Смолуховским (1906 г.). Проведенными исследованиями была окончательно доказана природа броуновского движения. Молекулы среды (жидкости или газа) сталкиваются с частицей дисперсной фазы, в результате чего она получает огромное число ударов со всех сторон.
Под микроскопом наблюдают проекцию смещения частицы на плоскость за какое-то время, поэтому При равновероятных отклонениях частицы ее направление будет находиться между направлениями x и у, т. е. под углом 45° к каждой координате. Отсюда Из-за равновероятных отклонений среднеарифметическое значение сдвигов равно нулю. Поэтому используются среднеквадратичные расстояния, проходимые частицей:
Эйнштейн и Смолуховский, постулируя единство природы броуновского движения и теплового движения, установили количественную связь между средним сдвигом частицы (называемым иногда амплитудой смещения) и коэффициентом диффузии D. Если броуновское движение является следствием теплового движения молекул среды, то можно говорить о тепловом движении частиц дисперсной фазы. Это означает, что дисперсная фаза, представляющая собой совокупность числа частиц, должна подчиняться тем же статистическим законам молекулярно-кинетической теории, приложимым к газам или растворам.
Так как |Q1| > |Q2| (ν1>ν2), то суммарное количество перенесенного вещества через плоскость MN вправо определится соотношением Градиент концентрации по расстоянию в направлении диффузии можно выразить так:
Подставляя, получим: Сравнивая это соотношение с первым законом диффузии Фика:
Это уравнение выражает закон Эйнштейна — Смолуховского, в соответствии с которым квадрат среднего сдвига пропорционален коэффициенту диффузии и времени.
Экзаменационный билет № 7
Диспергирование и конденсация — методы получения свободно-дисперсных систем: порошков, суспензий, золей, в том числе аэрозолей, эмульсий и т. д. Под диспергированием понимают дробление и измельчение вещества, под конденсацией — образование гетерогенной дисперсной системы из гомогенной в результате ассоциации молекул, атомов или ионов в агрегаты. Работа упругого и пластического деформирования пропорциональна объему тела: Работа образования новой поверхности при диспергировании пропорциональна приращению поверхности: Полная работа, затрачиваемая на диспергирование, выражается уравнением Ребиндера:
Разрушение материалов может быть облегчено при использовании эффекта Ребиндера — адсорбционного понижения прочности твердых тел. Этот эффект заключается в уменьшении поверхностной энергии с помощью поверхностно-активных веществ, в результате чего облегчается деформирование и разрушение твердого тела. Процесс конденсации предполагает образование новой фазы на уже имеющихся поверхностях (стенках сосуда, частицах посторонних веществ — ядрах конденсации) или на поверхности зародышей, возникающих самопроизвольно в результате флуктуации плотности и концентраций вещества в системе. В первом случае конденсация называется гетерогенной, во втором — гомогенной. Чтобы сконденсированное вещество не возвращалось в первоначальную фазу и конденсация продолжалась, исходная система должна быть пересыщенной. В противном случае конденсация не может происходить, исчезают и зародыши конденсации (путем их испарения, растворения, плавления). При гомогенной конденсации происходит самопроизвольное образование зародышей; энергия поверхности выступает в качестве потенциального барьера конденсации. Энергию Гиббса образования зародышей выражают (в соответствии с объединенным уравнением первого и второго начал термодинамики) в виде четырех составляющих: энтропийной, механической, поверхностной и химической. Для жидких и газообразных фаз можно ограничиться двумя первыми составляющими энергии Гиббса образования зародышей.
Если степень пересыщения больше критической величины, то возникающие зародыши будут самопроизвольно расти. Критическая энергия Гиббса образования зародышей конденсации соответствует критической точке — максимуму функции ΔG = f(r): Таким образом, энергия Гиббса образования зародышей при гомогенной конденсации равна одной трети поверхностной энергии зародыша. Если найти радиус зародыша в критической точке, приравняв к нулю первую производную от энергии Гиббса и подставить его в данное выражение, то получим:
Из этого соотношения следует, что энергия образования зародыша конденсации зависит от степени пересыщения, от нее же зависит и размер критического радиуса зародыша. Чем выше степень пересыщения, тем ниже энергия Гиббса образования зародышей и тем меньше размеры образующихся зародышей, способных к дальнейшему росту.
В золях через определенное, иногда очень длительное, время оседания частиц может наступить момент, когда диффузионный поток станет равным седиментационному iдиф = iсед, т.е. наступит диффузионно-седиментационное равновесие. Так как такое равновесие наступает пр |
Современная теория строения двойного электрического слоя основана на представлениях Штерна. Она объединяет две предыдущие теории. Согласно современной теории слой противоионов состоит из двух частей.
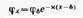
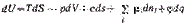
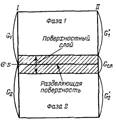Чтобы не определять границы поверхностного слоя (поверхности разрыва по Гиббсу), Гиббс предложил относить все изменения термодинамических параметров в слое в сравнении с параметрами объемной фазы к разделяющей поверхности, не имеющей объема или толщины (метод избыточных величин Гиббса). При таком рассмотрении поверхность характеризуется избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. Объемные фазы считаются однородными вплоть до разделяющей поверхности. В соответствии с методом избыточных величин энергия Гиббса системы равна сумме энергий Гиббса G1 и G2 объемных фаз 1, 2 и поверхностной энергии Гиббса σs, которая является избыточной: 
Для условия постоянства температуры это соотношение принимает вид
Современная теория строения двойного электрического слоя основана на представлениях Штерна. Она объединяет две предыдущие теории. Согласно современной теории слой противоионов состоит из двух частей.
Добавление в систему металл — вода раствора хлорида натрия приводит к избирательной адсорбции хлорид-анионов на поверхности металла. Появляется избыточный отрицательный заряд на поверхности металла и избыточный положительный заряд (ионы натрия) в близлежащем слое раствора, т. е. на межфазной поверхности образуется двойной электрический слой.
Рассчитайте время половинной коагуляции аэрозоля с дисперсностью частиц 2,5·108 м-1 и концентрацией 1,5·10-3 кг/м3, если константа быстрой коагуляции Смолуховского равна 3·10-19 м3/с. Плотность частиц аэрозоля примите равной 2200 кг/м3.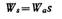
Чтобы получить соотношение между работой адгезии и поверхностными натяжениями взаимодействующих компонентов, представим себе две конденсированные фазы 2 и 3, имеющие поверхности на границе с воздухом 1, равные единице площади.
Угол θ, который образован касательными к межфазным поверхностям, ограничивающим смачивающую жидкость, имеющий вершину на линии раздела трех фаз, называется краевым углом, или углом смачивания.
в уравнении Дюпре заменить ее выражением нз закона Юнга
, получим
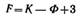
Рассмотрим результат влияния кривизны поверхности раздела между двумя несмешивающимися жидкостями на внутреннее давление в фазах.
и уравнение принимает вид 
.
Рассмотрим положение уровней жидкости в двух капиллярах, один из которых имеет лиофильную поверхность и поэтому стенки его смачиваются, у другого внутренняя поверхность лиофобизирована и не смачивается. В первом капилляре поверхность жидкости имеет отрицательную кривизну, поэтому дополнительное давление Лапласа стремится растянуть жидкость (давление направлено к центру кривизны) и поднимает ее в капилляре. Кривизна поверхности жидкости во втором капилляре положительна, дополнительное давление направлено внутрь жидкости, в результате жидкость в капилляре опускается (отрицательное капиллярное поднятие). При равновесии лапласовское давление равно гидростатическому давлению столба жидкости высотой h:
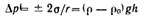
Нередко приходится наблюдать, как жидкость не может вытечь из капилляра под действием силы тяжести. Это объясняется проявлением действия капиллярного потенциала, направленного против силы тяжести, так как на нижнем конце капилляра жидкость образует мениск с положительной кривизной. Если часть капилляра, находящаяся над жидкостью, меньше высоты поднятия жидкости, жидкость из него не вытекает, так как кривизна мениска жидкости вверху капилляра становится положительной (положительный радиус кривизны), отвечающей гидростатическому давлению столба жидкости, равному размеру (высоте) капилляра, т. е. устанавливается равновесие.
.
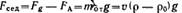
При седиментационном анализе дисперсности полидисперсных систем определяют время осаждения частиц отдельных фракций, рассчитывают скорости их осаждения и соответствующие им размеры частиц. Для этого сначала измеряют зависимость массы осевшего осадка от времени, строят график этой зависимости, называемой кривой седиментации, по которому затем определяют все необходимые характеристики дисперсной системы.
, 
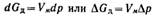
Эйнштейн и Смолуховский для количественного выражения броуновского движения частиц ввели представление о среднем сдвиге частицы. Если при наблюдении движения частицы золя под микроскопом через определенные равные промежутки времени отмечать ее местонахождение, то можно получить ее траекторию движения. Так как движение происходит в трехмерном пространстве, то квадрат среднего расстояния, проходимого частицей за любой промежуток времени, равен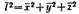 
.
.
или 
.
Для установления связи между средним сдвигом (смещением) частицы и коэффициентом диффузии представим себе трубку с поперечным сечением S, наполненную золем, концентрация частиц которого уменьшается слева направо. В этом же направлении протекает и диффузия частиц золя (на рисунке отмечено стрелкой). Выделим по обе стороны от линии MN два малых участка 1 и 2, размеры которых в направлении диффузии равны Δ — среднему квадратичному сдвигу за время τ. Обозначим частичную концентрацию золя в объемах этих участков соответственно через ν1 и ν2 (ν1>ν2). Хаотичность теплового движения приводит к равной вероятности переноса дисперсной фазы из обоих объемов вправо и влево от линии MN: половина частиц переместится вправо, а другая половина — влево. Количество дисперсной фазы за время τ переместится из объема 1 вправо: 
, а из объема 2 влево (в обратном направлении): 
.
.
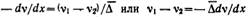
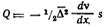
, окончательно имеем:
Если степень пересыщения меньше критической, то возникающие зародыши самопроизвольно испаряются (растворяются). Их размеры меньше критического, поэтому энергия Гиббса понижается с уменьшением размера зародыша. Пересыщенный раствор или пар в этих условиях иногда удобно представить как гетерогенно-дисперсную систему, в которой присутствует множество постоянно образующихся и исчезающих зародышей новой фазы. В критической точке неустойчивость равновесия проявляется в том, что существует равная вероятность возникновения и исчезновения зародышей конденсации.
