 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| IV. Экономическая интерпретация объективно обусловленных оценок и коэффициентов структурных сдвигов
На основании решения прямой задачи определим значение искомых переменных двойственной задачи. Коэффициенты индексной строки последней симплексной таблицы прямой задачи называются объективно-обусловленными оценками или двойственными оценками. Из последней симплекс-таблицы видим, что для переменных х4 и х5двойственные оценки равны соответственно 2 и 4. Дополнительные переменные вводились в ограничения по использованию сырья вида соответственно, тогда можно сказать, что значение переменных у1 и у2 двойственной задачи равно соответственно 2 и 4 д.е. Значение целевой функции для прямой и двойственной задачи одно и то же, равно 150 д.е. Если предприятие будет продавать сырье S1 и S2, то оно должно продавать его не ниже 2 д.е. вида S1 и 4 д.е. вида S2. Двойственные оценки основных переменных, не вошедших в базис, означают степень невыгодности использования данного вида ресурсов, либо степень нецелесообразности производства продукции. Для нашей задачи переменная х1 не вошла в базис. Двойственная оценка по переменной х1 равна 3. Если ввести дополнительно в оптимальный план одну единицу ресурсов, либо одну единицу производства какого-либо вида продукции, тогда значение целевой функции уменьшится на величину двойственной оценки при решении задачи на max и увеличится на ту же величину при решении задачи на min. Для нашего примера введем в оптимальный план одну единицу товара T1, тогда значение целевой функции С=150 – 3*1 = 147 д.е. А значения переменных оптимального плана будут Хопт.= {х1=1, х2=10, х3=5} Если ввести производства 2-ух единиц товара Т1, тогда С = 150 – 3*2 = 144 д.е. Хопт.= {х1=2, х2=10, х3=5}. Двойственные оценки при дополнительных переменных, не вошедших в базис (х4, х5) означают степень эффективности использования данных видов ресурсов. Если задача решается на max, то при введении дополнительно в опорный план 1 единицы ресурса значение целевой функции увеличивается на величину двойственной оценки, и, наоборот, при решении задачи на min– уменьшается на величину двойственной оценки. Если первоначальный объем сырья вида S1 увеличить с 35 ед. до 36 ед., тогда после решения задачи мы получим значение целевой функции: С = 150 + 2*1 = 152 д.е. Однако, вводить в оптимальный план необоснованное количество значений основных или дополнительных переменных неправильно, оптимальный план может нарушиться, поэтому существуют правила, по которым можно вводить максимально допустимые объемы введения в оптимальный план основных и дополнительных переменных величин. Если основная переменная не вошла в базис, тогда для определения максимально допустимого объема введения в базис основной переменной необходимо разделить значения базисных переменных на коэффициенты структурных сдвигов столбца основной переменной и выбрать среди полученных отрицательных отношений наибольшее. Оно определит максимально допустимый объем введения в базис основной переменной. Для определения максимально допустимого объема введения в базис дополнительной переменной, необходимо значения базисных переменных разделить на коэффициенты структурных сдвигов столбца этой переменной и среди полученных значений выбрать наибольшее положительное число. Оно определяет max объем. Пусть необходимо определить максимально допустимый объем введения в базис основной переменной х1, тогда составим отношение:
Среди отрицательных имеется одно отношение, равное -15, тогда максимально допустимый объем введения в оптимальный план производства продукции Т1 будет равен 15 единицам. Если же дополнительно в первоначальный опорный план к имеющемуся сырью добавлять определенное количество сырья, тогда оптимальный план будет меняться, при этом максимальный объем сырья, который можно добавить к исходному будет равен для сырья S1 = Максимальное количество вводимого сырья равно 15 д.е. Иначе вводить в оптимальный план дополнительно сырья S1 можно не более 15 единиц. Если ввести в оптимальный план дополнительно производство 15 ед. т/вара Т1 дополнительно, тогда значение целевой функции будет: С = 150 – 3*15 = 105 д.е. Если же ввести дополнительно ресурса S1 15 единиц, то С = 150 + 2*15 = 180д.е. Необходимо подчеркнуть, что при введении определенного количества значений основных или дополнительных переменных, значения базисных переменных должны изменяться. Каким образом можно рассчитать, какого будет значение базисных переменных при введении дополнительно к значениям переменных, не вошедших в базис, можно судить по коэффициентам структурных сдвигов? Коэффициенты структурных сдвигов – это коэффициенты в столбцах при переменных, не вошедших в базис (коэффициенты в столбцах х1, х4, х5). Если вводится в базис основная переменная с определенным значением, то, для того, чтобы определить, какое значение примут базисные переменные в оптимальном плане, необходимо объем вводимого значения основной переменной умножить на коэффициенты (соответствующие) структурных сдвигов и полученные произведения при знаке коэффициента структурного сдвига (-) прибавить к значению базисной переменной, и, если коэффициент структурного сдвига имеет знак «+», то вычесть из значения базисной переменной, полученной произведением Например, введем в оптимальный план производство 2-ух единиц товаров N1, тогда в новом оптимальном плане С = 150 – 2*3 =144 д.е. х1=2 х3=5+1/3*2= х2=10-8/3*2=14/3= хопт. = {х1=2, х3= Если в базис вводится некоторый объем дополнительной переменной, то для корректировки оптимального плана поступают следующим образом: Если коэффициент структурного сдвига имеет знак «-», тогда коэффициент структурного сдвига умножается на вводимый объем и полученное произведение вычитается из значения базисной переменной Если коэффициент структурного сдвига имеет знак «+», тогда значение коэффициента структурного сдвига умножается на вводимый объем и полученное произведение складывается со значением базисной переменной. Таким образом, использование двойственных оценок и коэффициентов структурных сдвигов дает возможность пользователю производить корректировку оптимального плана, не прибегая к повторному решению экономико-математической модели задач.
V. Использование двойственных оценок для анализа оптимального плана Как было сказано в Теме 1, решения задачи на ПК получают значения искомых переменных, значения целевой функции задачи и двойственной оценки. Двойственные оценки основных и дополнительных переменных позволяют пользователю эффективно проводить анализ полученного решения. Двойственные оценки дополнительных переменных иначе называют двойственными оценками ограничений. В зависимости от типа ограничений ≥, ≤, = - экономическая интерпретация их различна.
|



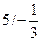 ,
, 
 , S2 =
, S2 =  .
.
