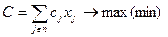ПОЗНАВАТЕЛЬНОЕ

Сила воли ведет к действию, а позитивные действия формируют позитивное отношение

Как определить диапазон голоса - ваш вокал

Игровые автоматы с быстрым выводом

Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими

Целительная привычка

Как самому избавиться от обидчивости

Противоречивые взгляды на качества, присущие мужчинам

Тренинг уверенности в себе

Вкуснейший "Салат из свеклы с чесноком"

Натюрморт и его изобразительные возможности

Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.

Как научиться брать на себя ответственность

Зачем нужны границы в отношениях с детьми?

Световозвращающие элементы на детской одежде

Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия

Как слышать голос Бога

Классификация ожирения по ИМТ (ВОЗ)

Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Запишем двойственную задачу к прямой задаче линейного программирования.

Понятие двойственности в экономико-математических моделях задач. Экономическая интерпретация прямых и двойственных задач.

1.Прямые и двойственные задачи. Правила построения двойственных задач.

2.Решение прямых задач с помощью симплекс-метода

3.Двойственный симплекс-метод

4.Экономическая интерпретация объективно обусловленных оценок и коэффициентов структурных сдвигов

5.Использование двойственных оценок для анализа оптимального плана

I. Прямые и двойственные задачи. Правила построения двойственных задач.

Рассмотрим построение прямой экономико-математической модели задачи на следующем примере общего вида.

Пусть предприятие имеет m видов экономических ресурсов, запасы которых соответственно равны b₁, b₂, …, b_m (iͼm), где i – номер экономического ресурса, m – множество, включающее в себя номера экономических ресурсов.

Известны нормы расхода каждого вида ресурса на одну единицу каждого вида продукции равные a_ij (iͼm; jͼn), где j – номер вида выпускаемой продукции, n – множество, включающее номера выпускаемой продукции.

Требуется составить такой план выпуска продукции, при котором предприятие получало бы максимальный экономический эффект, если известно, что экономический эффект от производства одной единицы j-ого вида продукции = c_j (jͼn).

Формализуем задачу.

Обозначим x_j (jͼn) – количество j-ого вида продукции, производимое предприятием в оптимальном плане. Тогда можно составить систему ограничений задачи по использованию каждого вида экономических ресурсов.

Ограничение по использованию первого вида ресурсов

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n ≤ b₁

Ограничение по использованию второго вида ресурса

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ + … + a_2nx_n ≤ b₂

… … … … … … … … … … … … … …

M) Ограничение по использованию m-ого вида ресурса

a_m1x₁ + a_m2x₂ + a_m3x₃ + … + a_mnx_n ≤ b_m

m+1) Ограничению по не отрицательности переменных величин

х₁≥0, х₂≥0, …, х_m ≥ 0

Целевая функция задачи - max экономического эффекта

Критерий оптимизации задачи может стремиться либо к максимуму, либо к минимуму.

С = с₁х₁ + с₂х₂ + … + с_nx_n ® max (min)

Вышезаписанную модель можно записать в сокращенном варианте:

1)

2)xj ≥0 (jͼn)

Развернутая и сокращенная форма записи не что иное, как запись прямой задачи линейного программирования. Однако к прямой задаче всегда существует двойственная задача.

Первоначально запишем правила построения двойственных задач:

1)Целевая функция прямой задачи обозначается буквой C, когда двойственная задача W, причем если целевая функция задачи (прямой) ® max, тогда двойственной задачи ® min и наоборот.

2)Если тип ограничения прямой задачи «≤», тогда двойственной задачи – «≥» и наоборот.

3) Свободные члены прямой задачи (b₁, b₂, …, b_m) выступают в качестве коэффициентов целевой функции двойственной задачи

4) Коэффициенты целевой функции прямой задачи являются свободными членами ограничений двойственной задачи

5) Число ограничений двойственной задачи = числу переменных прямой задачи

6) Технико-экономические коэффициенты двойственной задачи получают путем транспонирования матрицы технико-экономических коэффициентов прямой задачи

7)Если искомые переменныепрямой задачи обозначены x_j, тогда двойственные задачи – y_i

8) Технико-экономические коэффициенты двойственной задачи обозначают как b_ij, хотя в первоначальной записи можно использовать те же самые коэффициенты a_ij

Запишем двойственную задачу к прямой задаче линейного программирования.

a₁₁y₁ + a₂₁y₂ + … + a_m1y_m ≥ C₁

a₁₂y₁ + a₂₂y₂ + … + a_m2y_m ≥ C₂

a_1ny₁ + a_2ny₂ + … + a_mny_m ≥ C_n

y_i ≥ 0 (i = 1,2, …, m)

W = b₁y₁ + b₂y₂ + … + b_my_m ® min (max)

Чтобы понять экономический смысл двойственной задачи необходимо рассмотреть конкретный пример.

Пусть предприятие производит 3 вида продукции: Т₁, Т₂, Т₃. После того, как выполнено годовое задание у предприятия осталось сырье 2-ух видов S₁ и S₂, из которых производятся вышеназванные товары Т₁, Т₂, Т₃. Возникает вопрос, как поступить с остатками сырья:

1) Производить товары вновь

2) Продать остатки сырья какой-либо нуждающейся организации

Что выгоднее? Произвести продукцию и продать ее или продать сырье?

Числовые данные о наличии сырья, расходе сырья на одну единицу каждого вида продукции, прибыль от реализации каждого вида даны в таблице:

Рассмотрим такой случай, когда предприятие из остатков сырья будет производить продукцию и ее реализовать, получая прибыль.