 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Расчет разветвленных цепей с несколькими источниками
Если известна конфигурация сложной электрической цепи и заданы свойства всех составляющих ее элементов, то расчет такой цепи обычно сводится к определению токов в ветвях и потенциалов узлов. В отличие от рассмотренных выше случаев, разветвленная цепь с несколькими источниками требует специальных методов расчета. Следует отметить, что разветвленные цепи с одним источником так же можно рассчитывать рассмотренными ниже методами. Число неизвестных токов совпадает с числом m ветвей. Если в некоторых ветвях содержатся источники тока, то неизвестными для этих ветвей являются соответствующие UJ .Таким образом, для расчета цепи в общем случае следует составить систему из m независимых уравнений. Метод уравнений Кирхгофа Отыскание неизвестных величин связано с составлением и совместным решением системы уравнений, записанных по I и II законам Кирхгофа. Для того, чтобы записать эти уравнения, необходимо предварительно пронумеровать узлы, присвоив каждому из них соответствующее значение потенциала (j1, j2, ¼, jn) и ветви, присвоив каждой из них значение тока (I1, I2, ¼, Im). Прежде чем приступить к составлению уравнений по законам Кирхгофа, необходимо установить, сколько независимых уравнений составляется по каждому из этих законов. Уравнения по I закону Кирхгофа, связывающие m неизвестных токов, могут быть записаны для каждого из узлов цепи. Однако использовать для совместного решения можно только n–1уравнений, т.к. уравнение, записанное для последнего узла, окажется следствием всех предыдущих уравнений. По II закону Кирхгофа составляют число уравнений, равное числу ветвей m за вычетом числа уравнений, составленных по I закону Кирхгофа (n – 1), т.е. p = m – (n – 1) = m – n + 1, где p – количество независимых контуров. Все эти рассуждения справедливы для случая, когда в цепи содержатся источники тока. В этом случае уменьшается количество неизвестных токов, но появляется соответствующее число напряжений UJ, которые войдут в уравнения в качестве неизвестных величин. Таким образом, методика расчета разветвленной цепи, не содержащей источников тока, методом уравнений Кирхгофа следующая: 1. Обозначить токи ветвей и произвольно выбрать их положительное направление. 2. Произвольно выбрать опорный узел и совокупность p = m – n + 1 независимых контуров. 3. Для всех узлов, кроме опорного, составить уравнения по I закону Кирхгофа. Таких уравнений должно быть (n – 1). 4. Для каждого выбранного контура составить уравнения по II закону Кирхгофа. Таких уравнений должно быть p. 5. Система m уравнений Кирхгофа с m неизвестными токами решается совместно и определяются численные значения токов. 6. Если необходимо, рассчитать с помощью обобщенного закона Ома напряжения ветвей или разность потенциалов узлов. 7. Проверить правильность расчета с помощью баланса мощности. Если в цепи есть q источников тока, то при правильном выборе совокупности независимых контуров количество совместно решаемых уравнений в системе можно сократить на q. Если контуры выбирать таким образом, чтобы каждый источник тока вошел только в один контур, соответствующее UJ войдет только в одно уравнение по II закону Кирхгофа. Поскольку неизвестными являются только токи в (m – q) ветвях, количество уравнений по II закону Кирхгофа можно уменьшить до m – n + 1 – q. В результате, вместе с (n – 1) уравнением I закону Кирхгофа, получится система из m – q уравнений относительно неизвестных токов, после совместного решения которых оставшиеся q уравнений используются для определения Пример.
1. Обозначим токи ветвей. 2. Выбираем совокупность независимых контуров (I, II, III) и опорный узел с.
3. Уравнения по I закону Кирхгофа узел а: узел в: узел d: 4. Уравнения по II закону Кирхгофа I контур: II контур: III контур: 5. Совместно решаем систему из m – q = 5 уравнений относительно неизвестных токов I1, I2, I4, I5, I6, в которую не войдет уравнение. Составленное для II контура. 6. Определяем UJ. 7. Правильность расчетов проверяем с помощью баланса мощности
Метод контурных токов Метод контурных токов является одним из основных методов расчета сложных электрических цепей, которым широко пользуются на практике. При расчете методом контурных токов полагают, что в каждом независимом контуре течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего определяют токи ветвей через контурные токи. Таким образом, метод контурных токов можно определить как метод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по II закону Кирхгофа, т.е. Разработаем алгоритм расчета цепей методом контурных токов на примере приведенной на рис. 2.3. схемы, в которой три независимых контура. Предположим, что в каждом контуре протекает свой контурный ток в указанном направлении. Для каждого из контуров составим уравнения по II закону Кирхгофа. При этом учтем, что по смежной ветви для контурных токов
Тогда уравнения по II закону Кирхгофа для каждого контура принимают следующий вид:
Введем обозначения:
В окончательном виде система уравнений для контурных токов приобретает следующий вид:
в матричной форме
Собственное сопротивление контура (Rii) представляет собой арифметическую сумму сопротивлений всех потребителей, находящихся в i-ом контуре. Общее сопротивление контура (Rij = Rji) представляет собой алгебраическую сумму сопротивлений потребителей ветви (нескольких ветвей), одновременно принадлежащих i-ому и j-ому контурам. В эту сумму сопротивление входит со знаком «+», если контурные токи протекают через данное сопротивление в одном направлении (согласно), и знак «–», если они протекают встречно. Контурные ЭДС представляют собой алгебраическую сумму ЭДС источников, входящих в контур. Со знаком «+» в эту сумму входят ЭДС источников, действующих согласно с обходом контура, со знаком «–» входят ЭДС источников, действующих встречно. Решение полученной системы удобно выполнить методом Крамера
где D, D1, D2, D3, – соответственно определители матриц:
По найденным контурным токам при помощи I закона Кирхгофа определяются токи ветвей. Таким образом, методика расчета цепи постоянного тока методом контурных токов следующая: 1. Обозначить все токи ветвей и их положительное направление. 2. Произвольно выбрать совокупность p независимых контуров, нанести на схему положительное направление контурных токов, протекающих в выбранных контурах. 3. Определить собственные, общие сопротивления и контурные ЭДС и подставить их в систему уравнений вида (2.3). 4. Разрешить полученную систему уравнений относительно контурных токов, используя метод Крамера. 5. Определить токи ветвей через контурные токи по I закону Кирхгофа. 6. В случае необходимости, с помощью обобщенного закона Ома определить потенциалы узлов. 7. Проверить правильность расчетов при помощи баланса мощности. Если в цепи содержится q источников тока, количество совместно рассматриваемых уравнений сокращается на q и становится равным р – q, поскольку токи в таких ветвях известны (для контуров с Iii= J уравнение можно не записывать). В этом случае следует выбирать такую совокупность независимых контурных токов, чтобы часть из них стала известными. Для этого необходимо, чтобы каждый источник тока входил только в один контур. Напряжения UJисточников войдут в качестве неизвестных в правые части уравнений, т.е. в состав контурных ЭДС. Пример.
Тогда система уравнений по методу контурных токов примет следующий вид:
Причем, UJ можно определить из второго уравнения системы или, составив уравнение по II закону Кирхгофа для любого контура, в который входит источник тока. Баланс мощности:
Метод узловых потенциалов Ток в любой ветви схемы можно найти по обобщенному закону Ома. Для того, чтобы можно было применить закон Ома, необходимо знать значение потенциалов узлов схемы. Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов. Число неизвестных в методе узловых потенциалов равно числу уравнений, которые необходимо составить для схемы по I закону Кирхгофа. Метод узловых потенциалов, как и метод контурных токов, – один из основных расчетных методов. В том случае, когда п-1 < p (n – количество узлов, p – количество независимых контуров), данный метод более экономичен, чем метод контурных токов. Проиллюстрируем на простом примере получение методики расчета электрической цепи методом узловых потенциалов:
1. Записываем (n – 1) уравнение по I закону Кирхгофа (при выбранном опорном узле 4, потенциал которого условно принимаем равным нулю) узел 1: – I1 + I4 - I6 = 0 узел 2: I1 – I2 + J3 = 0 узел 3: I2 – I4 + I5 = 0 2. Для каждого из m токов записываем выражение по обобщенному закону Ома через потенциалы узлов с учетом, что потенциал j4 = 0:
3. Полученные в п. 2 выражения подставляем в уравнения, составленные по I закону Кирхгофа
Приведем подобные слагаемые при различных потенциалах и получим каноническую систему уравнений:
Введем обозначения:
В окончательном виде система уравнений для контурных токов приобретает следующий вид:
в матричной форме
Собственная проводимость узла (Gii) представляет собой арифметическую сумму проводимостей всех ветвей, соединенных в i-ом узле. Общая проводимость i-ого и j-ого узлов (Gij = Gji) представляет собой взятую со знаком «–» сумму проводимостей ветвей, присоединенных одновременно к i-ому и j-ому узлам. Проводимости ветвей с источниками тока полагаются равными нулю и в собственные и общие проводимости не входят! Узловой ток (Jii) состоит из двух алгебраических сумм: первая содержит токи источников тока, содержащиеся в ветвях, соединенных в i -ом узле; вторая представляет собой произведение ЭДС источников напряжения на проводимости соответствующих ветвей, соединенных в i -ом узле. Со знаком «+» в эту сумму входят E и J источников, действие которых направлено к узлу, со знаком «–» остальные. Решение системы уравнений по методу узловых потенциалов в общем случае выполняется методом Крамера при помощи определителей:
Тогда неизвестные потенциалы могут вычислены следующим образом:
Нетрудно, показать, что аналогичную систему уравнений можно построить для случая n узлов в цепи. Тогда необходимо составить для (n-1) узлов соответствующие уравнения, полагая потенциал n-ого узла, равным нулю. Таким образом, методика расчета цепи постоянного тока методом узловых потенциалов следующая: 1. Обозначить все токи ветвей и их положительное направление. 2. Произвольно выбрать опорный узел (jn)и пронумеровать все остальные (n-1)-e узлы. 3. Определить собственные и общие проводимости узлов, а также узловые токи, т.е. рассчитать коэффициенты в системе уравнений. 4. Записать систему уравнений в виде
Или в развернутом виде: алгебраическая форма
В этой системе каждому узлу соответствует отдельное уравнение. 5. Полученную систему уравнений решить относительно неизвестных (n – 1) потенциалов при помощи метода Крамера. 6. С помощью обобщенного закона Ома рассчитать неизвестные токи. 7. Проверить правильность расчетов при помощи баланса мощности. Порядок расчета не зависит от вида источников, действующих в цепи. Однако, расчет упрощается в случае, когда между одной или несколькими парами узлов включены идеализированные источники ЭДС. Тогда напряжения между этими парами узлов становятся известными величинами, определенными условиями задачи. Для успешного решения подобных задач необходимо правильно обозначить опорный узел, в качестве которого может быть выбран только один из узлов, к которым присоединена ветвь с идеализированным источником ЭДС. Если таких ветвей q, то количество уравнений в системе сократится до k = n – 1 – q. Пример. Если в данной схеме в качестве опорного узла выбрать узел 1 (j1=0), то потенциалы второго и третьего узлов можно считать известными и равными соответственно j2=E1и j3=E1–E2. Тогда неизвестным остается только потенциал четвертого узла, для которого составим уравнение по методу узловых потенциалов:
Следует отметить, что уравнения для 2 и 3 узлов составить не представляется возможным из-за появляющихся неопределенностей вида Подставим известные значения:
Из полученного уравнения найдем неизвестный Для разветвленной цепи, имеющей только два узла и произвольное количество ветвей, метод узловых потенциалов вырождается в метод двух узлов. Решение сводится к отысканию значения потенциала одного из узлов, т.к. потенциал другого узла может быть принятым равным нулю. Система уравнений превращается в одно уравнение:
при условии, что После определения U12 токи ветвей и напряжения источников тока находят при помощи обобщенного закона Ома. Пример.
Пусть
По обобщенному закону Ома:
Метод наложения Линейная электрическая цепь описывается системой линейных уравнений Кирхгофа. Это означает, что она подчиняется принципу наложения (суперпозиции), согласно которому совместное действие всех источников в электрической цепи совпадает с суммой действий каждого из них в отдельности. Так как принцип наложения следует из общих свойств линейных уравнений, то его можно применять для определения любых физических величин, которые связаны между собой линейной зависимостью. В применении к электрическим цепям можно определить не только токи при заданных сопротивлениях, ЭДС и токах источников, но и напряжения при заданных токах и известных сопротивлениях. Методом нельзя пользоваться для определения мощности, так как мощность квадратичная функция тока или напряжения и принципу суперпозиции не подчиняется. Метод наложения опирается на принцип наложения и заключается в следующем: ток или напряжение произвольной ветви или участка разветвленной электрической цепи постоянного тока определяется как алгебраическая сумма токов или напряжений, вызванных каждым из источников в отдельности. При использовании этого метода задача расчета разветвленной электрической цепи с n источниками сводится к совместному решению n цепей с одним источником. Методика расчета линейной электрической цепи методом наложения: 1. Произвольно задать направление токов в ветвях исследуемой цепи. 2. Исходную цепь, содержащую n источников, преобразовать в n подсхем, каждая из которых содержит только один из источников, прочие источники исключаются следующим образом: источники напряжения замыкаются накоротко, а ветви с источниками тока обрываются. При этом необходимо помнить, что внутренние сопротивления реальных источников играют роль потребителей и поэтому они должны оставаться в подсхемах. 3. Определить токи каждой из подсхем, задавшись их направлением в соответствии с полярностью источника, любым из известных методом. В большинстве случаев расчет ведется по закону Ома с использованием метода эквивалентных преобразований пассивных цепей. 4. Полный ток в любой ветви исходной цепи определяется как алгебраическая сумма токов вспомогательных подсхем, причем при суммировании со знаком «+» берутся токи подсхем, направление которых совпадает с направлением тока в исходной цепи, со знаком «–» – остальные. К достоинствам метода относят то обстоятельство, что расчет производится по частям, где составляющие тока и напряжения определяются довольно просто. Однако, поскольку решение предполагает произведение множества преобразований, метод не рекомендуется применять для схем, содержащих большое количество источников. Пример. Определить ток I2 в цепи, изображенной на рис. 2.8, а. Для данной цепи должны быть изображены две расчетные подсхемы (рис. 2.8, б и в). С помощью подсхемы 1 (рис. 2.8. б) найдем составляющую
Направление тока в подсхеме 1 совпадает с направлением искомого тока.
С помощью подсхемы 2 (рис. 2.8. в) найдем составляющую I2Е.
Направление тока в подсхеме 2 противоположно направлению искомого тока. Ток в исходной цепи определится следующим образом: |



 .
.







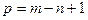 . Следовательно, этот метод более экономичен при вычислениях, чем метод уравнений Кирхгофа.
. Следовательно, этот метод более экономичен при вычислениях, чем метод уравнений Кирхгофа. и
и  (ветвь bd, содержащая сопротивление
(ветвь bd, содержащая сопротивление  ) протекает ток
) протекает ток  , по смежной ветви для контурных токов
, по смежной ветви для контурных токов  и
и  ) протекает ток
) протекает ток  , по смежной ветви для контурных токов
, по смежной ветви для контурных токов  ) протекает ток
) протекает ток  .
.
 Сгруппируем слагаемые при одноименных токах:
Сгруппируем слагаемые при одноименных токах: (2.5)
(2.5)
 (2.6)
(2.6) (2.7)
(2.7) , (2.8)
, (2.8)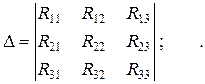
 (2.9)
(2.9)


 , решив первое уравнение, можно получить
, решив первое уравнение, можно получить  . Далее
. Далее 




 (2.10)
(2.10)


 (2.11)
(2.11) (2.12)
(2.12)
 (2.14)
(2.14) – матричная форма
– матричная форма


 , т.к. сопротивление ветви, содержащей идеализированный источник ЭДС, равно нулю, а проводимость соответственно
, т.к. сопротивление ветви, содержащей идеализированный источник ЭДС, равно нулю, а проводимость соответственно 
 , а далее и все токи.
, а далее и все токи. (2.15)
(2.15)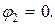

 , тогда
, тогда
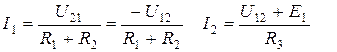

 по формуле о токах в двух параллельных ветвях
по формуле о токах в двух параллельных ветвях


