 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Преобразование линейных пассивных электрических цепей
Эквивалентное преобразование части пассивной электрической цепи состоит в такой ее замене другой пассивной цепью, при которой остаются неизменными токи и напряжения остальной цепи, не подвергшейся преобразованию. К простейшим преобразованиям относятся замена последовательно и параллельно соединенных потребителей эквивалентным потребителем. При последовательном соединении роль эквивалентного сопротивления (или сопротивления эквивалентного потребителя) играет сумма сопротивлений всех потребителей (рис. 1.11.).
При двух последовательно соединенных потребителях:
При параллельном соединении роль эквивалентной проводимости (или проводимости эквивалентного потребителя) играет сумма проводимостей всех потребителей (рис. 1.12.).
Это следует из I закона Кирхгофа:
Таким образом, для расчета цепей с последовательно включенными потребителями целесообразно их свойства выражать значениями сопротивлений, а для параллельно включенных – значениями проводимостей. Определение эквивалентного сопротивления при смешанном соединении потребителей выполняется путем постепенного упрощения (сворачивания) исходной цепи. Пример.
1. Параллельное соединение R1 и R2:
2. Последовательное соединение R12 и R3: 3. Последовательное соединение R4 и R5: 4. Параллельное соединение R123 и R45: 5. Последовательное соединение Rас и R6: Таким образом, эквивалентное сопротивление
Более сложными являются взаимные преобразования потребителей, соединенных звездой или треугольником. К таким преобразованиям следует обращаться в тех случаях, когда в цепи, подлежащей упрощению, нельзя выделить параллельное или последовательное соединения потребителей.
В узлах a, b, c и треугольник , и звезда на рис. 1.14. соединяются с остальной частью схемы. Преобразование треугольника в звезду должно быть таковым, чтобы при одинаковых значениях потенциалов одноименных точек треугольника и звезды притекающие к этим точкам токи были одинаковы, тогда вся внешняя схема «не заметит» произведенной замены. Выразим Uabтреугольника через параметры потребителей и притекающие к этим узлам токи. Запишем уравнения Кирхгофа для контура и узлов a и b.
Заменим в первом уравнении токи I3 и I2на соответствующие выражения:
По закону Ома напряжение Uab для соединения потребителей треугольником:
Теперь получим выражение для этого же напряжения при соединении потребителей звездой:
Для эквивалентности данных цепей при произвольных значениях токов Iaи Ib необходимо равенство напряжений Uabдля соединения потребителей треугольником и звездой. Это возможно только при одинаковых коэффициентах уравнений (1.15) и (1.16), т.е.
Аналогично можно получить выражения для определения
Таким образом, сопротивление луча звезды равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений трех сторон треугольника. Формулы обратного преобразования можно вывести независимо, либо как следствие соотношений (1.17) и (1.18) через проводимости:
или через сопротивления:
Следовательно, сопротивление стороны треугольника равно сумме сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча. Обобщенный закон Ома Рассмотрим закон Ома для участка цепи, содержащего активные и пассивные элементы. Пусть на неразветвленном участке 1-3 сложной цепи (рис. 1.15), содержащей источник и потребитель энергии, протекает ток I.
Для определения потенциала любой точки электрической цепи необходимо произвольно задать потенциал какой-нибудь одной точки. Пусть для рассматриваемой схемы Объединив эти две формулы, получаем:
Отсюда ток
Рассуждая аналогичным образом, можно получить выражение обобщенного закона Ома для случая противодействующего источника ЭДС: Объединив эти две формулы в одну, получим:
где верхний знак соответствует ветви с содействующим источником ЭДС, а нижний – с противодействующим. Выведенная формула представляет собой закон Ома для участка цепи с ЭДС или обобщенный закон Ома. Если в результате расчета по формуле (1.22) ток получает отрицательное значение, это означает, что действительное направление тока противоположно выбранному направлению. Обобщенный закон Ома можно вывести для ветви, содержащей источник тока (рис. 1.17). Для содействующего (рис. 1.17, а) источника тока
Для противодействующего (рис. 1.17, б) источника тока
Объединенная форма обобщенного закона Ома для ветвей, содержащих источник тока:
где верхний знак соответствуют схеме, на которой UJ и J сонаправлены. Баланс мощности Прохождение электрического тока по проводнику сопровождается выделением тепла. Согласно закону Джоуля-Ленца, вся электрическая энергия, сообщаемая проводнику в результате работы сил электрического поля, превращается в тепловую энергию. С помощью закона Ома можно записать для потребителя с сопротивлением R:
Обычно под законом Джоуля-Ленца понимают уравнение, определяющее не энергию, а мощность тепловых потерь
В приведенных выражениях тепловая энергия и мощность выражаются в Джоулях [Дж]и Ваттах [Вт] соответственно. Сформулированный закон распространяется на ветви, содержащие как пассивные, так и активные элементы. С этой целью пользуются обобщенным законом Ома (1.24)
Выражения (1.29), записанные для ветви с источником напряжения, справедливы и для ветви с источником тока, если произвести подстановку Отсюда следует закон сохранения энергии, согласно которому алгебраическая сумма мощностей, подводимых ко всем ветвям разветвленной электрической цепи, равна нулю:
Существует еще одна форма записи баланса мощности:
В левой части суммируются мощности источников энергии, а в правой – мощности, преобразованные в потребителях в тепло. Мощности источников, отдающих энергию, берутся со знаком «+», а работающих в режиме потребителей – со знаком «–» (рис. 1.18.).
Иногда пользуются уравнением баланса мощности в арифметической форме
Здесь мощности противодействующих источников считаются положительными, но при балансе учитываются как мощности потребителей. |




 (1.10) Это следует из II закона Кирхгофа:
(1.10) Это следует из II закона Кирхгофа: (1.11)
(1.11) (1.12)
(1.12)
 . (1.13)
. (1.13) При двух параллельно соединенных потребителях:
При двух параллельно соединенных потребителях: (1.14)
(1.14)









 (1.15)
(1.15) (1.16)
(1.16) (1.17)
(1.17) :
: (1.18)
(1.18) (1.19)
(1.19) (1.20)
(1.20)
 . Потенциал точки 2 больше потенциала точки 1 на значение ЭДС:
. Потенциал точки 2 больше потенциала точки 1 на значение ЭДС:  . Ток I в любом пассивном элементе цепи направлен от точки с более высоким потенциалом до точки с более низким потенциалом. Поэтому потенциал точки 3 меньше потенциала точки 2, т.е.
. Ток I в любом пассивном элементе цепи направлен от точки с более высоким потенциалом до точки с более низким потенциалом. Поэтому потенциал точки 3 меньше потенциала точки 2, т.е.  .
. (1.21)
(1.21) (1.22)
(1.22)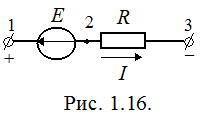
 (1.23)
(1.23) , (1.24)
, (1.24)



 (1.25)
(1.25) (1.26)
(1.26) (1.27)
(1.27) (1.29)
(1.29) вместо
вместо  и
и  вместо
вместо  .
. (1.30)
(1.30) . (1.31)
. (1.31)
 . (1.32)
. (1.32)