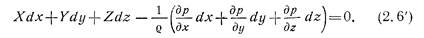 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ
ОСНОВЫ ГИДРОСТАТИКИ
СВОЙСТВА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ В покоящейся жидкости возможен лишь один вид напряжений - напряжение сжатия, т. е. гидростатическое давление. Необходимо иметь в виду следующие два свойства гидростатического давления в жидкости: 1. На внешней поверхности жидкости гидростатическое давление всегда направлено по нормали внутрь рассматриваемого объема жидкости. Это свойство непосредственно вытекает из определения давления, как напряжения нормальной сжимающей силы. Под внешней поверхностью жидкости следует понимать не только поверхности раздела ее с внешней средой, но и поверхности элементарных объемов, мысленно выделяемых нами из общего объема жидкости. 2. В любой точке внутри жидкости гидростатическое давление по всем направлениям одинаково, т. е. давление не зависит от угла наклона площадки, на которую оно действует в данной точке.
Пусть вблизи выделенного объема на жидкость действует единичная массовая сила, составляющие которой равны X, Y и Z. Обозначим через рх гидростатическое давление, действующее на грань, нормальную к оси ох, через ру—давление на грань, нормальную к оси оу, и т. д. Гидростатическое давление, действующее на наклонную грань, обозначим через рn,а площадь этой грани - через dS. Все эти давления направлены по нормалям к соответствующим площадкам. Имеем
Свойство гидростатического давления в неподвижной жидкости имеет место также при движении невязкой жидкости. При движении же вязкой жидкости возникают касательные напряжения, вследствие чего гидромеханическое давление в вязкой жидкости указанным свойством, строго говоря, не обладает. ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ Рассмотрим тот основной случай равновесия жидкости, когда из числа массовых сил на жидкость действует лишь сила тяжести, и получим для этого случая уравнение, позволяющее находить величину гидростатического давления в любой точке рассматриваемого объема жидкости. Свободная поверхность жидкости в этом случае, как известно, является горизонтальной плоскостью. Пусть жидкость содержится в сосуде (рис. 6) и на ее свободную поверхность действует давление ро. Найдем величину гидростатического давления р в произвольно взятой точке М, расположенной на глубине h. У точки М, как центра, возьмем элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет являться внешним давлением и будет направлено по нормали внутрь объема, т. е. вверх. Запишем сумму всех сил, действующих на рассматриваемый объем в вертикальном направлении. Будем иметь
где последний член представляет собой вес жидкости в указанном объеме. Силы давления на боковой поверхности цилиндра в уравнение не войдут, так как они нормальны к этой поверхности. Сократив на dS и перегруппировав члевы, получим p=po+hy. (2.2) Полученное уравнение называют основным уравнением гидростатики; оно позволяет подсчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления на внешней поверхности жидко Величина ро является одинаковой для всех точек объема жидкости, поэтому, учитывая второе свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково (закон Паскаля). Давление жидкости, как видно из формулы (2.2), растет с увеличением глубины по закону прямой, и на данной глубине есть величина постоянная. Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня. В данном случае поверхностями уровня являются горизонтальные плоскости, а свободная поверхность является одной из поверхностей уровня. Возьмем на произвольной высоте горизонтальную плоскость сравнения, от которой вертикально вверх будем отсчитывать координаты z. Обозначив через z координату точки М, через z0—координату свободной поверхности жидкости и заменив в уравнении (2.2) h на z0—z, получим
Но так как точка М нами взята произвольно, то, можно утверждать, что для всего рассматриваемого неподвижного объема жидкости
Координата z называется нивелирной высотой. Величина p/g имеет также линейную размерность и называется пьезометрической высотой. Сумма z+p/g называется гидростатическим напором. Таким образом, гидростатический напор есть величина постоянная для всего объема неподвижной жидкости.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ ЖИДКОСТИ Получим дифференциальные уравнения равновесия жидкости в общем случае, когда на жидкость действует не только сила тяжести, но и другие массовые силы, например, силы инерции переносного движения при так называемом относительном покое. В неподвижной жидкости возьмем произвольную точку М с координатами х, у и z и давлением р. Выделим в жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллельными координатным осям и соответственно равными dx, dy и dz. Точка М пусть будет одной из вершин выделенного параллелепипеда (рис. 7). Рассмотрим условия равновесия выделенного объема жидкости. Пусть в выделенном объеме на жидкость действует результирующая массовая сила, составляющие которой, отнесенные к единице массы, равны X, Y и Z. Тогда массовые силы, дейст На выделенный параллелепипед будут действовать лишь указанные массовые силы и разности сил давления. Поэтому уравнения равновесия параллелепипеда в направлениях трех координатных осей запишутся в следующем виде:
В пределе получим уравнения равновесия жидкости, отнесенные к точке М
Система дифференциальных уравнений гидростатики (2.5) называется уравнениями Эйлера. Для практического пользования удобнее вместо системы уравнений (2.5) получить одно эквивалентное им уравнение, не содержащее частных производных.
Трехчлен, заключенный в скобках, представляет собой полный дифференциал давления, т. е. функции р(х, у, z). Поэтому уравнение (2.6') можно переписать в следующем виде;
Полученное уравнение выражает приращение давления dp, обусловленное изменением координат на величины dx, dy и dz, в самом общем случае равновесия жидкости.
|
Выделим в неподвижной жидкости элементарный объем в форме прямоугольного тетраэдра с ребрами, параллельными координатным осям и соответственно равными dx, dy и dz (рис. 5).
сти ро и давления, обусловленного весом вышележащих слоев жидкости.
вующие на выделенный объем в направлении координатных осей, будут равны этим составляющим, умноженным на массу выделенного объема.
