 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Методы решения систем линейных алгебраических уравнений 12
Расчет установившихся режимов электрических систем 1.схема замещения электрической сети не содержит замкнутых контуров Индивидуальное задание Для схемы, представленной на рис.1 найти токи в ветвях разомкнутой электрической сети, используя матричную форму записи 1-го закона Кирхгофа. Токи нагрузки заданы в таблице 1. Рис. 1 Таблица 1
Данный раздел должен содержать: · краткие теоретические сведения, · обобщенное уравнение состояния, · вычисление обратной матрицы для матрицы · вычисление обратной матрицы для матрицы · вычисление токов в ветвях аналитическим методом и с помощью MATLAB- программы, 1.краткие теоретические сведения 2.обобщенное уравнение состояния
Уравнение (1) объединяет два матричных уравнения. Уравнение по первому закону Кирхгофа
Уравнение по второму закону Кирхгофа
3.вычисление обратной матрицы для матрицы 1) Записываем матрицу
2) Заменяем каждый элемент матрицы
3) Этот определитель сопровождаем знаком плюс, если сумма индексов элемента четная, и знаком минус – в противном случае.
4)Делим полученную матрицу на вычислением определитель классическим методом
4. вычисление обратной матрицы для матрицы >> M=[-1,1,1;0,-1,0;0,0,-1]; >> inv(M)
ans =
-1 -1 -1 0 -1 0 0 0 -1 5. вычисление токов в ветвях аналитическим методом и с помощью MATLAB- программы 1) аналитическим методом
2)с помощью MATLAB- программы
>> J=[5+i*6;5+i*6;3+i*4]; >> Minv=[-1,-1,-1;0,-1,0;0,0,-1]; >> -Minv*J
ans =
13.0000 +16.0000i 5.0000 + 6.0000i 3.0000 + 4.0000i 2.схема замещения электрической сети содержит замкнутые контуры Индивидуальное задание Для схемы представленной на рис.2 определить токи в ветвях схемы, напряжения в узлах. Сеть трехфазная. Рис. 2 Таблица 2
Данный раздел должен содержать: · краткие теоретические сведения, · первую и вторую матрицы инциденций, · обобщенное уравнение состояния, · решение матричного уравнения состояния двумя способами (методом обратной матрицы, методом Гаусса), · решение матричного уравнения состояния методом Крамера в системе MATLAB, · сравнение полученных промежуточных результатов, найденных разными способами, · вычисление узловых напряжений аналитически, · нахождение узловых напряжений с помощью MATLAB- программы, · сравнение полученных результатов, найденных разными способами.
1.краткие теоретические сведения
2. первая и вторая матрица инциденций
Первая матрица инциденций без балансирующего узла будет иметь вид:
В нашей схеме замещения всего один независимый контур, в соответствии с этим вторая матрица инциденций примет вид:
3.обобщенное уравнение состояния
[1,-1,0,0;-1,0,0,-1;0,0,-1,1;-1,-2,3,2] 4.решение матричного уравнения состояния двумя способами (методом обратной матрицы, методом Гаусса) 1) метод обратной матрицы
Находим решение с помощьюMATLAB Обозначим матрицу
а обратную
>> m=[1,-1,0,0;-1,0,0,-1;0,0,-1,1;-1,-2,3,2]; >> minv=inv(m); >> F=[-50;-100;-100;0]; >> I=minv*F
I =
87.5000 137.5000 112.5000 12.5000
2) метод Гаусса Пусть I12=x1;I14=x2;I34=x3;I23=x4; Тогда запишем систему уравнений
На главной диагонали, преобразованной матрицы коэффициентов, стоят 1. Теперь проведем преобразования в соответствии с обратным ходом метода Гаусса. Из последнего уравнения системы определяем
В результате получаем вектор-столбец искомых неизвестных
5.решение матричного уравнения состояния методом Крамера в системе MATLAB
>> d=[1,-1,0,0;-1,0,0,-1;0,0,-1,1;-1,-2,3,2]; >> d1=[-50,-1,0,0;-100,0,0,-1;-100,0,-1,1;0,-2,3,2]; >> d2=[1,-50,0,0;-1,-100,0,-1;0,-100,-1,1;-1,0,3,2]; >> d3=[1,-1,-50,0;-1,0,-100,-1;0,0,-100,1;-1,-2,0,2]; >> d4=[1,-1,0,-50;-1,0,0,-100;0,0,-1,-100;-1,-2,3,0]; >> det(d) ans = >> det(d1) ans = >> det(d2) ans = >> det(d3) ans = >> det(d4) ans = >> x1=det(d1)/det(d) x1 = 87.5000 >> x2=det(d2)/det(d) x2 = 137.5000 >> x3=det(d3)/det(d) x3 = 112.5000
>> x4=det(d4)/det(d) x4 = 12.5000
6.сравнение полученных промежуточных результатов, найденных разными способами
После сравнения мы види, что все токи абсолютно идентичны 7.вычисление узловых напряжений аналитически По закону Ома определим падение напряжения на ветвях схемы
Используя уравнение
Перемножая матрицы в матричном уравнении, получаем
8.нахождение узловых напряжений с помощью MATLAB- программы Вычеркиваем из матрицы Mt последнюю строку и из матрицы Uв аналогично. >> m=[1,-1,0;-1,0,0;0,0,-1]; >> UB=[87.5;275;337.5]; >> inv(m)*UB
ans =
-275.0000 -362.5000 -337.5000 Отсюда следует, что
9.сравнение полученных результатов, найденных разными способами
Методы решения систем линейных алгебраических уравнений Индивидуальное задание
Данный раздел должен содержать: · краткие теоретические сведения, · исследование системы линейных алгебраических уравнений на совместность, · аналитическое решение системы линейных алгебраических уравнений методом Гаусса, · решение системы линейных алгебраических уравнений методом Жордана-Гаусса в системе MATLAB, · сравнение полученных результатов, найденных разными способами. 1.краткие теоретические сведения 2.исследованием системы линейных алгебраических уравнений на совместность Для этого вычислим ранг матрицы коэффициентов >> A=[2, -1, 1, -1;2, -1, 0,-3;3 -1, 1, 1;1, 2, -4, 5]; rank(A) ans = 4 >> A1=[2, -1, 1, -1, 1; 2 ,- 1, 0,- 3,5;3,-1, 1, 1, -3;1, 2, -4, 5, -6]; rank(A1) ans = 4 Получили, что ранг матрицы коэффициентов равен рангу расширенной матрицы коэффициентов, отсюда следует, что система совместна и имеет единственное решение (ранги матриц равны порядку системы). 3.аналитическое решение системы линейных алгебраических уравнений методом Гаусса
На главной диагонали, преобразованной матрицы коэффициентов, стоят 1. Теперь проведем преобразования в соответствии с обратным ходом метода Гаусса. Из последнего уравнения системы определяем
В результате получаем вектор-столбец искомых неизвестных
4. решение системы линейных алгебраических уравнений методом Жордана-Гаусса в системе MATLAB >> A=[1 2 -4 5;2 -1 1 -1;2 -1 0 -3;3 -1 1 1]; B=[-6;1;5;-3]; >> AB=[A B]
AB =
1 2 -4 5 -6 2 -1 1 -1 1 2 -1 0 -3 5 3 -1 1 1 -3 >> rref(AB)
ans =
1.0000 0 0 0 1.3333 0 1.0000 0 0 5.6667 0 0 1.0000 0 1.3333 0 0 0 1.0000 -2.6667
>> X=(A\B)'
X = 1.3333 5.6667 1.3333 -2.6667 5. сравнение полученных результатов, найденных разными способами
После сравнения мы видим, что корни системы, полученные методом Гаусса абсолютно идентичны корням, полученным с помощью методом Жордана-Гаусса в системе MATLAB.
12 |










 классическим методом
классическим методом в системе MATLAB
в системе MATLAB (1)
(1)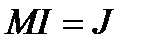 .
. 
 ,
,


 , транспонированную к матрице M.
, транспонированную к матрице M.

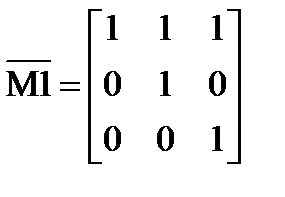
 определитель матрицы M.
определитель матрицы M.




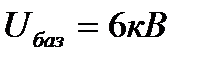 . Исходные данные по вариантам заданы в таблице 2.
. Исходные данные по вариантам заданы в таблице 2.

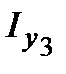





 .
. .
.





 ,
,






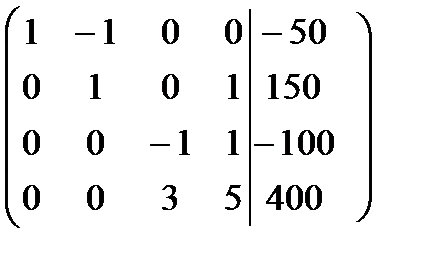


 . Из предпоследнего уравнения находим
. Из предпоследнего уравнения находим  . Проведя аналогичные вычисления, получаем
. Проведя аналогичные вычисления, получаем 













 , получаем
, получаем
 уравнения с
уравнения с  неизвестными, т.е. данная система переопределена. В нашем случае можно выбросить любое уравнение переопределенной системы и решить ее также каким-либо методом решения систем линейных алгебраических уравнений.
неизвестными, т.е. данная система переопределена. В нашем случае можно выбросить любое уравнение переопределенной системы и решить ее также каким-либо методом решения систем линейных алгебраических уравнений.








 и ранг расширенной матрицы коэффициентов. Для этого воспользуемся системой MATLAB.
и ранг расширенной матрицы коэффициентов. Для этого воспользуемся системой MATLAB.













 . Из предпоследнего уравнения находим
. Из предпоследнего уравнения находим  . Проведя аналогичные вычисления, получаем
. Проведя аналогичные вычисления, получаем 

