 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Расчёт сложных цепей с помощью правил Кирхгофа (общий метод расчёта)
ИТНИТ ИБ ЭЛЕКТРОТЕХНИКА РАБОТА № 1
РАСЧЁТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА Основные понятия Упорядоченное движение заряженных частиц называется электрическим током. Его принято характеризовать силой тока - скалярной величиной, равной заряду, проходящему через поперечное сечение проводника в единицу времени. Если за время dt проходит заряд dq, то сила тока I по определению равна:
Единица силы тока - Ампер. Для получения тока в каком-либо проводнике на его концах необходимо создать и поддерживать разность потенциалов. Поскольку под действием электростатического поля заряды перемещаются так, чтобы разность потенциалов уменьшалось, необходимы устройства, в которых на заряды действовали бы силы, отличные от сил электростатического поля. Такие силы получили название сторонних сил. Всякие устройства, в которых возникают сторонние силы, называются источниками тока (например, гальванические элементы и т. п.). Сторонние силы могут быть обусловлены химическими процессами, диффузией носителей заряда в неоднородной среде, электрическими (не потенциальными) полями. Сторонние силы можно охарактеризовать работой, которую они совершают над перемещающимися по цепи зарядами. Величина, равная работе сторонних сил, отнесенной к единице положительного заряда, называется электродвижущей силой (ЭДС) ε, действующей в цепи или на её участке. Следовательно, если работа сторонних сил над зарядомq равна A, то по определению:
Размерность ЭДС совпадает с размерностью потенциала. Электрической цепью называется совокупность источников тока, соединительных проводов, приборов или других устройств (активных и реактивных сопротивлений). В настоящей работе рассматриваются методы расчёта сложных разветвлённых цепей, содержащих источники ЭДС, соединительные провода и резисторы (сопротивления). Рассчитать такую цепь означает найти значения токов через все резисторы, зная номиналы резисторов и значения всех ЭДС,а также (иногда) и некоторые значения напряжений и мощностей. Для расчёта цепей постоянного тока используют закон Ома и правила Кирхгофа.
Законы постоянного тока Закон Ома для участка цепи Георг Ом экспериментально установил закон, согласно которому сила тока, текущего по проводнику, в котором не действуют сторонние силы, прямо пропорциональна напряжению на концах проводника.
Величина σ- коэффициент пропорциональности - называется проводимостью проводника, величина, обратная проводимости, называется сопротивлением проводника:
Размерность сопротивления [ Ом ], согласно (3) и (4) [Ом] = [В/А]. Размерность проводимости – [Сименс]. Закон Ома для электрической цепи (для полной цепи) Напряжение U на концах участка цепи, содержащего источник ЭДС величиной Е и резистор сопротивлением R, через который протекает ток I ,равно алгебраической сумме Е и I∙R, при этом следует учитывать и внутреннее сопротивление источника ЭДС. Правила Кирхгофа В практике часто встречаются разветвленные цепи, т.е. цепи, состоящие из нескольких включенных параллельно, последовательно приборов, устройств или сопротивлений. Расчет таких цепей значительно упрощается, если пользоваться правилами, сформулированными Кирхгофом. Первое правило относится к узлам цепи. Узлом цепи называется точка, в которой соединяются более двух проводников. Первое правило Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю:
Выделим теперь в разветвленной цепи какой-либо замкнутый контур. К отдельным участкам этого контура можно применить закон Ома для участка цепи. Можно показать, что для любого замкнутого участка цепи справедливо уравнение:
которое выражает второе правило Кирхгофа:для любого замкнутого контура сумма всех падений напряжений равна сумме всех электродвижущих сил в этом контуре. Уравнение (6) выполняется для всех замкнутых контуров, которые можно мысленно выделить в данной разветвлённой цепи. Методы расчёта цепей Расчёт сложных цепей с помощью правил Кирхгофа (общий метод расчёта) Рассмотрим цепь на рисунке 1:
Пусть задача состоит в определении направлений и значений всех токов через резисторы, исходя из заданных значений ЭДС (Е с соответствующим номером) и сопротивлений резисторов. За направление тока примем направление движения условных положительных зарядов. (в этом случае говорят, что ток течёт от «плюса» к «минусу». Число неизвестных токов равно 6, поэтому нужно составить 6 независимых уравнений, связывающих значения этих токов, используя правила Кирхгофа. При составлении уравнений учитывают направления токов в ветвях схемы, а так как токи неизвестны, то предварительно произвольно выбирают эти направления, с таким расчётом, чтобы для каждого из узлов некоторые токи входили в него, а некоторые выходили (по направлению стрелок на схеме). Составляя уравнения по первому правилу Кирхгофа, следует токи, приходящие к узлу и уходящие от него, брать с разными знаками. В нашем случае будем брать токи, приходящие к узлам, с положительным знаком, а токи, выходящие из узла – с отрицательным знаком. При составлении уравнений по второму правилу Кирхгофа ЭДС и токи, направления которых совпадают с произвольно выбранным направлением обхода контура, обычно берут с положительным знаком, остальные – с отрицательным. Для узлов А, В и С составим уравнения по первому правилу Кирхгофа: Для узла А: i1 – i4 –i6 = 0 ,для узла В: i4 + i5 – i2 = 0 , для узла С: i6 – i3 – i5 = 0 Для последнего из выбранных в схеме узла Д уравнения не составляем, ибо оно не будет независимым, так как оно может быть получено путём суммирования уравнений для рассмотренных ранее узлов. В общем случае, для сложной цепи, содержащей N узлов, составляют не более N – 1 уравнений по первому правилу Кирхгофа. Недостающие уравнения (в нашем случае – три) составляют по второму правилу Кирхгофа для произвольно выделенных в цепи независимых контуров (вследствие чего уравнения будут также независимыми). Контуры считаются независимыми, если в каждом из них имеется хотя бы одна ветвь, не принадлежащая другим контурам. Для нашей схемы выберем три указанных на рисунке контура и условимся направлением их обхода считать направление по часовой стрелке. Согласно второму правилу Кирхгофа, имеем: Для контура 1: - E1 = - i2R2 – i4R4 – i1R1 Для контура 2: - E2 = - i3R3 + i5R5 + i2R2 Для контура 3: -E3 = i4R4 – i5R5 – i6R6 Решая полученную систему из 6 уравнений известными из алгебры способами (обычно по методу определителей и матриц), находим все неизвестные токи. Если вычисленное значение какого – либо тока окажется отрицательным, то это указывает на то, что действительное направление тока противоположно произвольно выбранному. После определения токов в цепях можно, если это требуется, вычислить напряжения и мощности в схеме. Рассмотренный метод нагляден и позволяет сразу же определить значения токов, но для сложных схем трудоёмок, так как требуется решать системы из большого числа уравнений. Поэтому в ряде случаев используют и другие методы расчёта. Рассмотрим некоторые из них.
|
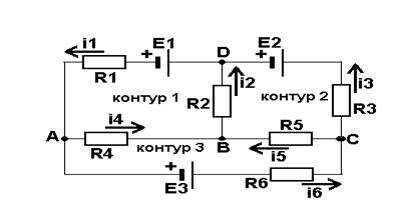Рисунок 1