ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Рекурсія. Обхід дерев. Префіксна та постфіксна форми запису виразів
Об'єкт називають рекурсивним, якщо він містить сам себе чи його означено за допомогою самого себе. Рекурсія — потужний засіб у математичних означеннях. Приклад 2.5.У підрозділі 2.1 сформульовано означення повного бінарного дерева. Тепер означимо його рекурсивно: а) о (ізольована вершина) — повне бінарне дерево; б) якщо А та В — повні бінарні дерева, то конструкція, зображена на рис. 2.7, — повне бінарне дерево.
Рис. 2.7 Схема рекурсії
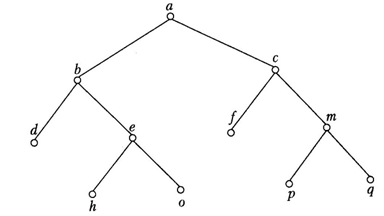
Приклад 2.6.Рекурсивне означення функції п\ для невід'ємних цілих чисел має такий вигляд: а) 0!=1; б) якщо п > 0, то п!=п(п-1)!. Очевидно, що важливість рекурсії пов'язана з тим, що вона дає змогу означити нескінченну множину об'єктів за допомогою скінченного висловлювання. Так само нескінченні обчислення можна описати за допомогою скінченної рекурсивноі програми, навіть якщо вона не містить явних циклів. Проте найдоцільніше використовувати рекурсивні алгоритми тоді, коли розв’язувану задачу, обчислювану функцію чи оброблювані дані задано за допомогою рекурсії. Чимало задач можна моделювати з використанням кореневих дерев. Поширене таке загальне формулювання задачі: виконати задану операцію D з кожною вершиною дерева. Тут D — параметр загальнішої задачі відвідування всіх вершин, або так званого обходу дерева. Розглядаючи розв'язування цієї задачі як єдиний послідовний процес відвідування вершин дерева в певному порядку, можна вважати їх розміщеними одна за одною. Опис багатьох алгоритмів істотно спрощується, якщо можна говорити про наступну вершину дерева, маючи на увазі якесь упорядкування. Є три принципи впорядкування вершин, які природно випливають зі структури дерева. Як і саму деревоподібну структуру, їх зручно формулювати за допомогою рекурсії. Звертаючись до бінарного дерева, де R — корінь, А та В — ліве та праве піддерева (рис. 2.7), можна означити такі впорядкування. 1. Обхід у прямому порядку (preorder), або зверху вниз: R, А, В (корінь відвідують до обходу піддерев). 2. Обхід у внутрішньому порядку (inorder), або зліва направо: А, R, В. 3. Обхід у зворотному порядку (postorder), або знизу вверх: А, В, R (корінь відвідують після обходу піддерев). Приклад 2.7. На рис. 2.8 зображено бінарне дерево. Різні обходи дадуть такі послідовності вершин: ♦ обхід у прямому порядку: a b d e h o c f m p q; ♦ обхід у внутрішньому порядку: d b h e o a f c pm q; ♦ обхід у зворотному порядку: d h o e b f p q m c a.
Рис. 2.8 Обхід дерева
Зазначені способи обходу бінарних дерев можна узагальнити й на довільні m-арні дерева. Обхід таких дерев у прямому порядку (зверху вниз) схематично зображено на рис. 2.9, у внутрішньому порядку (зліва направо) — на рис. 2.10, у зворотному (знизу вверх) —на рис. 2.11.
Рис. 2.9 Крок 1 обходу дерева
Рис. 2.10 Крок 2 обходу дерева
Рис. 2.11 Крок 3 обходу дерева
Надзвичайно поширене в інформатиці застосування обходу дерев — зіставлення виразам (арифметичним, логічним тощо) дерев і побудова на цій основі різних форм запису виразів. Суть справи зручно пояснити на прикладі. Розглянемо арифметичний вираз:
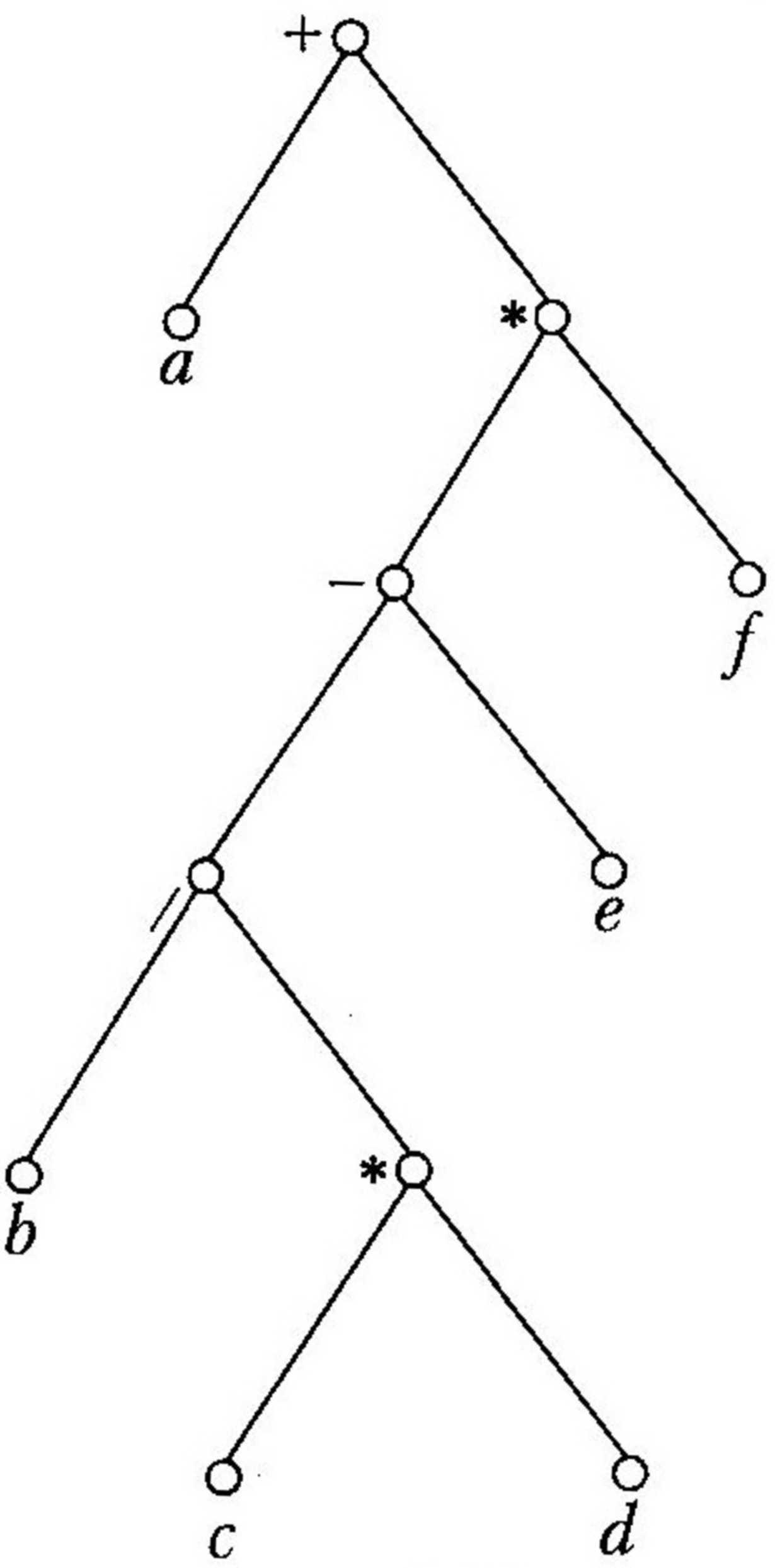
Подамо його у вигляді дерева. Послідовність дій відтворено на рис. 2.12. Рамкою на ньому обведено дерево, яке відповідає заданому арифметичному виразу. Внутрішнім вершинам цього дерева відповідають символи операцій, а листкам — операнди.
Рис. 2.12 Подання виразу за допомогою дерева
Обійдемо це дерево, записуючи символи у вершинах у тому порядку, у якому вони зустрічаються в разі заданого способу обходу. Отримаємо такі три послідовності: · ♦ у разі обходу в прямому порядку — префіксиий (польський) запис *+а/bc-d*ef; ♦ у разі обходу у внутрішньому порядку — інфіксний запис (поки що без дужок, потрібних для визначення порядку операцій) а+b/с*d-e*f; ♦ у разі обходу в зворотному порядку — постфіксний (зворотний польський) запис abс/+def*-*. Звернімося спочатку до інфіксної форми запису виразу. Без дужок вона неоднозначна: один запис може відповідати різним деревам. Наприклад, дереву, зображеному на рис. 2.13, у разі обходу зліва направо відповідає той самий вираз а+b/с*d-e*f, що й дереву на рис. 2.12 (у рамці), хоча на цих рисунках зображено різні дерева. Щоб уникнути неоднозначності інфіксної форми, використовують круглі дужки щоразу, коли зустрічають операцію. Повністю „одужкований" вираз, одержаний під час обходу дерева у внутрішньому порядку, називають ін-фіксною формою запису. Отже, для дерева з рис. 2.12 інфіксна форма така: ((а+ +(b/с))*(d-(e*/))), а для дерева, зображеного на рис. 2.13, інфіксна форма має такий вигляд: (a+(((b/(с* d))-e)*f)).
Рис. 2.13. Подання виразу деревом
Наведені міркування свідчать, що інфіксна форма запису виразів незручна. На практиці використовують префіксну та постфіксну форми, бо вони однозначно відповідають виразу й не потребують дужок. Ці форми запису називають польським записом (на честь польського математика й логіка Яна Лукасевича, українця за походженням). Приклад 2.8. Розглянемо логічний вираз ((p^q))~(р vq). Послідовні етапи побудови відповідного бінарного дерева зображено на рис. 2.14.
Рис. 4.14. Побудова математичного дерева
Отримаємо такі форми запису виразу: ♦ інфіксна форма запису (відповідає обходу дерева виразу у внутрішньому порядку): (((p^q))~((p)v(q))); ♦ польський запис (відповідає обходу дерева виразу в прямому порядку): ~^pqvpqvpq; ♦ зворотний польський запис (відповідає обходу дерева виразу в зворотному порядку): pq^рqv~.
Для обчислення значення виразу в польському записі його проглядають справа наліво та знаходять два операнди разом зі знаком операції перед ними. Ці опе-ранди та знак операції вилучають із запису, виконують операцію, а її результат записують на місце вилучених символів. Приклад4.9.Обчислимо значення виразу в польському записі (стрілка означає піднесення до степеня) +–*235/234. За сформульованим правилом виділимо 23, ці символи вилучимо й обчислимо 23=8; результат запишемо на місце вилучених символів: +–*235/84. Продовжимо обчислення. Динаміку процесу відображено в табл. 4.1. Таблиця 4.1
Для обчислення значення виразу в зворотному польському записі його прогля-дають зліва направо та виділяють два операнди разом зі знаком операції після них. Ці операнди та знак операції вилучають із запису, виконують операцію, а її результат записують на місце вилучених символів. Приклад4.10. Обчислимо значення виразу в зворотному польському записі 723*–493/+. Динаміку обчислень відображено в табл. 4.2. Таблиця 4.2
Бінарне дерево пошуку
Бінарне дерево забезпечує дуже зручний метод організації даних, у разі використання якого можна легко знайти будь-які конкретні дані чи виявити, що їх немає. Очевидно, що найнеефективніший спосіб пошуку — послідовний перегляд усіх даних. Справді, якщо потрібних даних немає, то для виявлення цього потрібно переглянути весь список. Бінарне дерево пошуку дає змогу уникнути цього. Єдина вимога — уведення для даних якогось лінійного порядку. Ним може бути, наприклад, алфавітний або числовий порядок. Лінійно впорядкувати можна теги, покажчики, файли чи інші ключі, які визначають дані. Але нас цікавитиме лише наявність якогось лінійного порядку. У бінарному дереві пошуку кожній вершині присвоєно значення, яке називають ключем. Ключ — це елемент якоїсь лінійно впорядкованої множини: будь-які два її елементи можна порівняти (див. підрозділ 5.3). Під час побудови бінарного дерева пошуку використовують його рекурсивну властивість, яку можна описати так. Кожна вершина розбиває дерево на два піддерева. Ліве піддерево містить лише ключі, менші від ключа цієї вершини, а праве — ключі, більші від ключа вершини. Ця властивість повторюється для кожної вершини (рис. 4.15, 4.16).
Рис. 4.15 Рекурсивне розбиття дерева
Рис. 4.16 Рекурсивне розбиття дерева Розглянемо алгоритм додавання об'єкта до дерева пошуку, який будує бінарне дерево пошуку. Почнемо з дерева, що містить лише одну вершину. Означимо її як корінь. Перший об'єкт списку присвоюємо кореню; це ключ кореня. Щоб додати новий об'єкт, виконуємо таку процедуру. |