 ПОЗНАВАТЕЛЬНОЕ
| Бектрекінг (пошук із поверненнями)
Опишемо загальний метод, який дає змогу значно зменшити обсяг обчисленьв алгоритмах типу повного перебору всіх можливостей. Щоб застосувати цейметод, розв'язок задачі повинен мати вигляд скінченної послідовності (х1, хп).Головна ідея методу полягає в тому, що розв'язок будують поступово, починаю-чи з порожньої послідовності X (довжиною 0). Загалом, якщо є частковий (не-повний) розв'язок (х1, хп), де і < п, то намагаємося знайти таке допустимезначення х1+1, що можна продовжувати (хи хі+і) до одержання повного роз-в'язку. Якщо таке допустиме, але ще не використане значення хі+, існує, то до-лучаємо цю нову компоненту до часткового розв'язку та продовжуємо процесдля послідовності (хь ...,xitxi+i). Якщо такого значення хі+і немає, то повертає-мося до попередньої послідовності (х„ ж,-1) і продовжуємо процес, шукаючинове, іще не використане значення х\. Тому процес називають бектрекінгом(англ. backtracking — пошук із поверненнями). Роботу цього алгоритму можна інтерпретувати як процес обходу якогось дерева.Кожна його вершина відповідає якійсь послідовності {хх,xt), причому верши- ни, які відповідають послідовностям вигляду (хі.....Хі, у), - сини цієї вершини. Корінь дерева відповідає порожній послідовності. Виконується обхід цього дерева пошуком углиб. Орім того, задають предикат Р, означений на всіх вершинах дерева. Якщо P(v) = F, то вершини піддерева з ко-ренем у вершині v не розглядають, і обсяг перебору зменшується. ПредикатP(v) набуває значення F тоді, коли стає зрозумілим, що послідовність (хь х{),яка відповідає вершині v, ніяким способом не можна добудувати до повногорозв'язку. Проілюструємо застосування алгоритму бектрекінг на конкретних прикладах. Приклад 4.15. Побудова гамільтонових циклів у графі [23]. Починаємо з довільноївершини. Будуємо шлях без повторення вершин, доки це можливо. Якщо вдалося про-йти всі вершини, то перевіряємо, чи існує ребро, що з'єднує останню й початкову верши-ни цього шляху. Якщо описаний процес у певний момент неможливо продовжити, топовертаємося на одну вершину назад і намагаємося продовжити побудову шляху (безповторення вершин) іншим способом. Пошук усіх гамільтонових циклів у графі з п'ятьма вершинами (рис. 4.29) можна проілюструвати за допомогою дерева, зображеного на рис. 4.30. Роботу алгоритму почато зодноелементної послідовності, бо в циклі вибір першої вершини неістотний. Розв'язки задачі обведено, і до них у прямокутних рамках приписано відповідні гамільтонові цикли.Отже, замість побудови й аналізу 5! = 120 послідовностей довжиною 5 вершин графа,зображеного на рис. 4.28, ми розглянули лише 23 послідовності довжиною від 1 до 5.
Рисунок 4.28. Алгоритм бектрекінгу при розфарбовуванні графу
Приклад 4.16. Розфарбовування графа в и кольорів. Нехай вершини графа позначено як а, b, с,.... Спочатку розфарбуємо вершину а в колір 1, а потім — вершину b в той самий колір, якщо b не суміжна з вершиною а, а ні, то розфарбуємо вершину b в колір 2. Перейдемо до третьої вершини с. Використаємо для вершини с колір 1, якщо це можливо, а ні, то колір 2, якщо це можливо. Тільки якщо жоден із кольорів 1 і 2 не можна використовувати, розфарбуємо вершину с в колір 3. Продовжимо цей процес, доки це можливо, використовуючи один з п кольорів для кожної нової вершини, причому завжди братимемо перший можливий колір зі списку кольорів. Досягнувши вершини, яку неможна розфарбувати в жоден з п кольорів, повертаємося до останньої розфарбованої,відміняємо її колір і присвоюємо наступний можливий колір зі списку. Якщо й це неможливо, то ще раз повертаємося до попередньої вершини, відміняємо її колір і намагаємося присвоїти новий колір, наступний можливий зі списку. Цей процес продовжуємо аналогічно. Якщо розфарбування в п кольорів існує, то така процедура дає змогу знайти його. На рис. 4.31 зображено граф і процес присвоювання трьох кольорів вершинам із використанням алгоритму бектрекінг.
Приклад 4.17. Задача про N ферзів. Як п ферзів можна розмістити на шахівниці п ферзя так, щоб жодні два не били один одного? Для розв'язання цієї задачі потрібно визначити n позицій на шахівниці так, щоб жодні дві позиції не були в одному рядку,в одному стовпці та на одній діагоналі. Діагональ містить усі позиції з координатами такі, що і +j=m для якогось т, або i-j=m (тут і — номер рядка,;' — номер стовпця). Починаємо з порожньої шахівниці. На (&+1)-му кроці намагаємося розмістити нового ферзя в (& + 1)-му стовпці, причому в перших k стовпцях уже є ферзі. Перевіряємо клітинки в (k + 1)-му стовпці, починаючи з верхньої. Шукаємо таку позицію для ферзя, щоб він небув у рядку та на діагоналі з тими ферзями, які вже є на шахівниці. Якщо це неможливо, то повертаємося до місця ферзя на попередньому k-му кроці та розміщаємо цього ферзя на наступному можливому рядку в цьому k-му стовпці, якщо такий рядок є, а ні,то повертаємося до ферзя в (&-1)-му стовпці. Алгоритм бектрекінг для я = 4 проілюстровано на рис. 4.32. Кожній вершині дерева на рис. 4.32 відповідає послідовність довжиною від 0 до 4. її k-кчлен дорівнює номеру клітинки з ферзем у k-му стовпці. Наприклад, вершинам шляху,який веде до розв'язку, відповідають такі послідовності: X, (2), (2, 4), (2, 4, 1), (2, 4, 1, 3)
Приклад 4.18. Суми елементів підмножин.Задано множину натуральних чисел ( х1 ,х2, хn). Потрібно знайти її підмножину, сума елементів якої дорівнює заданому числу М. Починаємо з порожньої множини. Нагромаджуємо суму, послідовно добираючи доданки. Число з послідовності х1,х2, хn долучають до суми, якщо сума після додавання цього числа не перевищує М. Якщо сума настільки велика, що додавання будь-якого нового числа перевищує Приклад 4.19. Побудова всіх максимальних незалежних множин вершин у простому графі G = (V, Г) [20, 35]. Тут граф подано як пару, утворену множиною вершин Прямий крок від
Крок повернення від
Якщо множина вершин Sk максимальна, то Доцільно намагатися почати кроки повернення якомога раніше, бо це обмежить розміри „непотрібної” частини дерева пошуку. У зв'язку з цим зауважимо таке. Нехай
Алгоритм побудови всіх максимальних незалежних множин вершин у простому графі G = (V, Г) Наведемо кроки алгоритму. Крок 1. Ініціалізація. Виконати Крок 2. Прямий крок. Вибрати вершину Крок 3. Перевірка. Якщо виконано умову Крок 4. Якщо Крок 5. Крок повернення. Виконати Унаслідок зв'язку між кліками й незалежними множинами (див. теорему 3.21) цей алгоритм можна використати також і для побудови максимальних клік. Карка |






 , то повертаємось і змінюємо останній доданок у сумі. На рис. 4.33 проілюстровано алгоритм бектрєкінг для задачі відшукання підмножини множини {31, 27, 15, 11, 7, 5} із сумою 39.
, то повертаємось і змінюємо останній доданок у сумі. На рис. 4.33 проілюстровано алгоритм бектрєкінг для задачі відшукання підмножини множини {31, 27, 15, 11, 7, 5} із сумою 39. та відповідністю
та відповідністю  , котра показує, як зв'язані між собою вершини (див. підрозділ 3.3). Почнемо з порожньої множини й будемо додавати до неї вершини зі збереженням незалежності. Нехай
, котра показує, як зв'язані між собою вершини (див. підрозділ 3.3). Почнемо з порожньої множини й будемо додавати до неї вершини зі збереженням незалежності. Нехай  — уже отримана множина з k вершин,
— уже отримана множина з k вершин,  — множина вершин, котрі можна додати до
— множина вершин, котрі можна додати до  ø. Серед вершин
ø. Серед вершин  розрізняють ті, котрі вже було використано для розширення
розрізняють ті, котрі вже було використано для розширення  ), і ті, котрі ще не використано (їх позначають
), і ті, котрі ще не використано (їх позначають  ). Загальна схема алгоритму бектрекінг для задачі побудови максимальних незалежних множин вершин у простому графі має такий вигляд.
). Загальна схема алгоритму бектрекінг для задачі побудови максимальних незалежних множин вершин у простому графі має такий вигляд. до
до  полягає у виборі вершини
полягає у виборі вершини 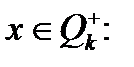


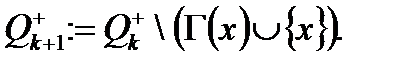
 до
до 



 ø. Якщо
ø. Якщо  ø, то множину
ø, то множину 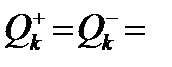 ø.
ø.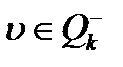 і
і  ø. Цю вершину неможливо вилучить з
ø. Цю вершину неможливо вилучить з 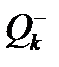 , оскільки можна вилучати лише вершини, суміжні з вершинами множини
, оскільки можна вилучати лише вершини, суміжні з вершинами множини 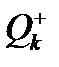 . Отже, існування такої вершини
. Отже, існування такої вершини  , що
, що  і
і  ø — достатня умова для повернення. Окрім того,
ø — достатня умова для повернення. Окрім того,  .
. ø,
ø,  ø,
ø,  ,
,  .
. і побудувати, як описано вище, множини
і побудувати, як описано вище, множини  ,
,  ,
,  ; при цьому залишити
; при цьому залишити  та
та  без змін. Виконати
без змін. Виконати  .
. ø, то перейти до кроку 5, інакше до кроку 4.
ø, то перейти до кроку 5, інакше до кроку 4. ø. то надрукувати максимальну незалежну множину
ø. то надрукувати максимальну незалежну множину  ø, а
ø, а  ø, то перейти до кроку 5. Інакше перейти до кроку 2.
ø, то перейти до кроку 5. Інакше перейти до кроку 2. . Вилучити вершину
. Вилучити вершину  із
із  , щоб одержати
, щоб одержати  із множини
із множини  та
та  ø, то зупинитися (на цей момент уже буде надруковано всі максимальні незалежні множини). Інакше перейти до кроку 3.
ø, то зупинитися (на цей момент уже буде надруковано всі максимальні незалежні множини). Інакше перейти до кроку 3.